33. Автокорреляционная функция и коррелограмма.

Автокорреляционная функция - это характеристика сигнала, которая помогает находить повторяющиеся участки сигнала или определять несущую частоту сигнала, скрытую из-за наложений шума и колебаний на других частотах. Автокорреляционная функция часто используется в обработке сигналов и анализе временных рядов.

Неформально автокорреляционная функция - это сходство между значениями сигнала как функция от разницы во времени между ними. Количественно ее можно найти с помощью коэффициента корреляции между уровнями начального временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов по времени.

Определим коэффициент корреляции между рядами уt и yt-1. Формула для расчета коэффициента корреляции можно представить в виде: 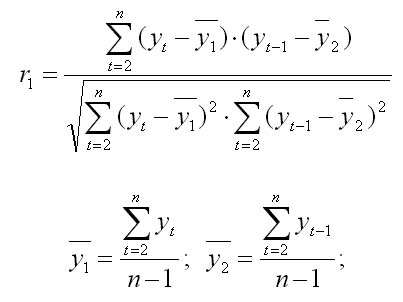Эта величина - коэффициент автокорреляции первого порядка, так как он определяет зависимость между соседними уровнями ряда t и t-1

Аналогично определяют коэффициенты автокорреляции второго и более высоких порядков.

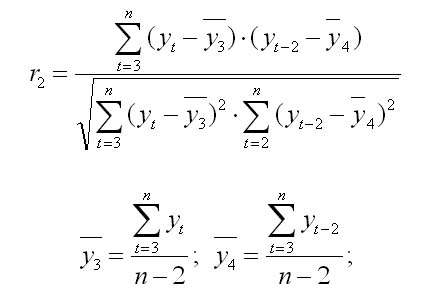
Число периодов, по которым определяется коэффициент автокорреляции, называют лаг автокорреляции. С ростом лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается что лаг должен определяться отношением n/4 - количество наблюдений деленных на 4.

В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:

и показывает связь сигнала (функции ) с копией самого себя, смещённого на величину τ.

Свойства коэффициента автокорреляции По коэффициенту автокорреляции судят о наличии линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (степенную функцию или экспоненту), коэффициент автокорреляции может быть меньше 0,7.

По знаку коэффициента автокорреляции нельзя делать судить о возрастающем или убывающем направлении связи в ряду.

Коррелограмма

Последовательность коэффициентов автокорреляции уровней первого, второго и других порядков называется автокорреляционной функцией временного ряда. График значений коэффициентов автокорреляции разных порядков называют коррелограммой.

Анализ автокорреляционной функции и коррелограммы позволяет найти лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями временного ряда наиболее тесная. Анализ коэффициентов автокорреляции

Если максимальным оказался коэффициент автокорреляции первого порядка, временной ряд содержит только тенденцию (тренд). Если максимальным оказался коэффициент автокорреляции порядка n, ряд содержит циклические колебания с периодичностью в n моментов времени.

Если ни один из коэффициентов автокорреляции не является значимым (близок к 0), можно сказать, что либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит нелинейную тенденцию, для выявления которой проводят дополнительный анализ.

Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию (AКФ), иными словами коэффициенты автокорреляции (и их стандартные ошибки) для последовательности лагов из определенного диапазона (например, от 1 до 30). На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, потому что интерес в основном представляют очень сильные (а, следовательно, высоко значимые) автокорреляции. Исследование коррелограмм. При изучении коррелограмм следует помнить, что автокорреляции последовательных лагов формально зависимы между собой. Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а второй с третьим, то первый элемент должен также каким-то образом зависеть от третьего и т.д. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка, т.е. после взятия разности с лагом 1. Взятие разности также удаляет тренд, который обычно подавляет другие автокорреляции. Например, если имеется устойчивый линейный тренд, как в ряде авиаперевозок, то каждое наблюдение в большой степени является линейной функцией предыдущего наблюдения.