№1 Понятие и практическое значение эконометрики.

Эконометрика - отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим отношениям.

Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика» (от гр. metron—мера). Таким образом, сам термин подчеркивает специфику, содержание эконометрики как науки: количественное выражение тех связей и соотношений, которые раскрыты и обоснованы экономической теорией. Эконометрика входит в обширное семейство дисциплин, посвящённых измерениям и применению статистических методов в различных областях науки и практики.

Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эта наука возникла в результате взаимодействия и объединения в особый «сплав» трех компонентов: экономической теории, статистических и математических методов. Впоследствии к ним присоединилась вычислительная техника как условие развития эконометрики. Эконометрика как система специфических методов начала развиваться с осознания своих задач — расчета количественных оценок, отражения особенностей экономических переменных и связей между ними.

В журнале «Эконометрика», основанном в 1933 г. Р. Фришем (1895-1973), дано следующее определение эконометрики: «Эконометрика - это не то же самое, что экономическая статистика. Она не идентична и тому, что мы называем экономической теорией, хотя значительная часть этой теории носит количественный характер. Эконометрика не является синонимом приложений математики к экономике. Как показывает опыт, каждая из трех отправных точек — статистика, экономическая теория и математика - необходимое, но не достаточное условие для понимания количественных соотношений в современной экономической жизни. Это единство всех трех составляющих. И это единство образует эконометрику».

Таким образом, эконометрика - это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.

Нельзя утверждать, что получено однозначное определение эконометрики. Так, Э. Маленво интерпретировал эконометрику как «любое приложение математики или статистических методов к изучению экономических явлений».

О. Ланге (1904-1965) писал, что эконометрика занимается определением наблюдаемых в экономической жизни конкретных количественных закономерностей, применяя для этой цели статистические методы. Статистический подход к эконометрическим измерениям стал доминирующим.

Практическое значение эконометрических моделей состоит в том, что они предоставляют основу для численного экспериментирования в изучаемом экономическом процессе. Меняя значения параметров в математической модели, будем получать разные исходы для представляемого этой моделью процесса. Это позволяет выбрать оптимальное экономическое решение из множества возможных, т. е. полученных в серии численных реализаций модели для разных параметров, входящих в неё.

Вплоть до 1970-х годов эконометрика понималась как эмпи­рическая оценка моделей, разработанных экономической теори­ей. Р. Фриш определял соотношение между теорией и данными наблюдений следующим образом: теория, абстрактно формулиру­ющая количественные соотношения, должна быть проверена множеством наблюдений. Свежие статистические данные и дру­гие факты должны защитить теорию от опасного догматизма. Под влиянием лидеров, таких, как Р. Фриш, Т. Хаавелмо, Я. Тинбер- ген, JI. Клейн, экономические модели, построенные в этот пери­од, всегда были кейнсианскими.

Все изменилось в 1970-е годы. В макроэкономике возникли противоречия между кейнсианцами, монетаристами и марксис­тами. Формальные методы стали использоваться для доказатель­ства причинности при выборе теоретических концепций. Эконо­мическая теория потеряла свое решающее значение.

Другое важное событие - появление компьютеров с высоким быстродействием и мощной оперативной памятью. Существен­ное развитие получил статистический анализ временных рядов. Г. Бокс и Г. Дженкинс создали ARIMA-модель в 1970 г., а К. Симе и другие ученые — VAR-модели, ставшие популярными в начале 1980-х гг.

Существенно стимулировало эконометрические исследова­ния развитие финансовых рынков и инструментов. Это привело к разработке моделей с использованием цензурированных дан­ных (Дж. Тобин).

№2. Связь эконометрики с другими областями научного знания.

Эконометрика (Econometrics) - совокупность методов анализа связей между различными экономическими показателями (факторами) на основании реальных статистических данных с использованием аппарата теории вероятностей и математической статистики. При помощи этих методов можно выявлять новые, ранее не известные связи, уточнять или отвергать гипотезы о существовании определенных связей между экономическими показателями, предлагаемые экономической теорией.

Необходимость решения эконометрических задач возникает в самых различных сферах экономики, н-р:

Анализ семейных бюджетов ( Уровень дохода семьи от её экономических и социально-демографических характеристик (количество работников в семье, количество иждивенцев, уровень образования и квалификация главы семьи и т.д.); Зависимость накоплений от уровня дохода и оценки имущества; Зависимость затрат на питание, одежду, транспортные издержки, путешествия и т.д. от дохода; Зависимость дохода индивидуума от уровня его образования и возраста; Зависимость потребления от дохода)

Анализ хозяйственной деятельности предприятий и их подразделений(Производственные функции – зависимости объёма производства от затрат труда и затрат капитала для предприятий некоторой отрасли; Зависимость производительности труда от объёма выпуска, энерговооружённости, заработной платы работников; Зависимость общих затрат и их составляющих (затрат на электроэнергию, цеховые расходы, РСЭО, износ инструмента и др.) от объёмов выпуска продукции нескольких видов; Зависимость производительности труда рабочих некоторой профессии от возраста и производственного стажа;Зависимость прибыли фирмы от затрат на обновление основных фондов)

Изучение спроса ( Зависимость спроса от цены на товар, цен замещающих и сопутствующих товаров, доходов покупателей;Зависимость рыночной цены на жильё от его параметров (площади жилых помещений, кухни, расположения, расстояния от центра, этажности, наличия телефона, балкона, лифта и т.д.; Зависимость цены на автомобиль от пробега, срока эксплуатации, состояния; Зависимость спроса на кредиты от процентной ставки)

Задачи налогообложения (Зависимость налоговых поступлений в бюджет от размера усреднённого совокупного налога (УСН), налога на прибыль – кривая Лаффера)

Задачи финансового рынка(Зависимость курса акций от курса валют, цен на нефть и лаговых переменных курса; Зависимость доходности ценных бумаг от рыночных индексов (ведущих факторов); Краткосрочное прогнозирование процентных ставок, курсов валют и т.д.)

Отраслевые задачи(Зависимость урожайности зерновых культур от уровня механизации (количества тракторов приведённоё мощности, комбайнов, орудий обработки почвы на 100 га), количества удобрений, химических средств защиты растений на 1 га; Зависимость количества врачей от количества населения, смертности от количества врачей и медсестёр на 1000 человек.)

Макроэкономический анализ (Зависимость темпа роста заработной платы от уровня безработицы (кривая Филипса) ;Взаимозависимость инвестиций, потребления, внутреннего валового продукта, денежной массы, процентной ставки по кредитам; Зависимость экспорта от ВНП; Зависимость объёма сбережений от доходов в предыдущем году и процентной ставки по депозитам;Зависимость потребления от дохода и процентной ставки по депозитам;Зависимость экспорта от импорта;Зависимость уровня инфляции от безработицы;Зависимость инвестиций от ВНП и процентной ставки;Зависимость роста заработной платы от производительности труда и уровня инфляции.)

Математика вторгается в эконометрику в 2х этапах:

1. При формировании теоретических взаимосвязей

2. При разработке или проверке статистических методов

№3. Основные направления экономических исследований.

В зависимости от того, в каком аспекте экономисты изучают свой предмет, могут быть выделены два подхода и, соответственно, два направления деятельности. Содержанием одного из них является позитивная экономика; содержанием второго — нормативная экономика.

Позитивная экономика исследует реальную экономическую жизнь. Она изучает те пути, которые различные экономические агенты фактически используют для достижения своих целей. Позитивные экономисты могут анализировать, какими методами компании действуют, чтобы получить максимальную прибыль, или как ведут себя домашние хозяйства, чтобы максимально удовлетворить свои потребительские запросы. В их отчетах отражаются сведения о том, что было, что имеет место сейчас и чего следует ожидать в будущем. Обоснованность сделанных ими заключений может быть легко проверена. Примерами выводов позитивной экономики могут служить утверждения о том, что с ростом банковской процентной ставки объем инвестиций сокращается, и о том, что с ростом безработицы уровень зарплаты падает.

Нормативная экономика занимается поиском наиболее эффективных путей достижения тех целей, которые общество ставит перед собой. При этом экономисты попадают под влияние политических рекомендаций и сталкиваются с этическими ограничениями, которые во многом определяют границы того, что следует делать и чего не следует. Экономистам приходится занимать вполне определенные моральные позиции, как по вопросам права собственности, так и по целям. Примерами заключений этого направления могут быть: "уровень безработицы следует снизить" или "распределение доходов должно быть более равномерным".

Строгой границы между этими двумя направлениями не существует, поскольку нормативные экономисты, давая ту или иную рекомендацию, должны определить пути, по которым ее можно реализовать, и уметь прогнозировать поведение реальных экономических агентов в изменившихся условиях, т.е. знать результаты исследований позитивной экономики.

№5. Парная регрессия

Парная регрессия характеризует связь между двумя признаками. Аналитически связь между ними описывается следующими уравнениями:

- прямой Y(X)=A₀ + A₁*X параболыY(X)=A₀+A₁*X+A₂*X

-гиперболы Y(X)=A₀+A₁+ 1/X

Определить тип уравнения можно в первую очередь графическим способом. Помимо этого существует более общее указание: если результативный и факторный признаки возрастают одинаково, то это свидетельствует о наличии линейной связи между ними. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая функция.

№6. Методы оценки качества моделей парных связей

Оценку качества построенной модели можно определить через коэффициент (индекс) детерминации, а также с помощью средней ошибки аппроксимации.

Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических в процентах:

.

Предел значений считаем допустимым при построении модели.

Средний коэффициент эластичночти показывает, на сколько % в среднем по совокупности изменится результат от своей средней величины при изменении фактора на 1% от своего среднего значения

- характеризует соотношение прироста результата и фактора для соответствующей формы связи.

Т.к., коэффициент Э не всегда const, то используем среднее значение - .

В таблице представлены формулы эластичности для наиболее употребительных функций.

y

Иногда коэффициент Э экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, изменение роста заработной платы с ростом стажа работы на 1%.

Если линеаризация не затрагивает зависимую переменную, например , то требование МНК: выполнимо, то (коэффициент корреляции совпадает с индексом корреляции), в этом легко убедиться.

Коэффициентом детерминации, или долей объясненной дисперсии называется

.

Введем обозначения:

TSS (total sum of sguares) – вся дисперсия: сумма квадратов отклонений от среднего.

RSS (regression sum of sguares) – объясненная часть всей дисперсии (обусловленная

регрессией), факторная, объясненная дисперсия.

ESS (error sum of sguares) – остаточная сумма, дисперсия остаточная.

В силу определения .

Если , то это означает, что регрессия ничего не дает, т.е. не улучшает качество предсказания , по сравнению с тривиальным .

Если , то лежат на линии регрессии и между и y существует линейная функциональная зависимость, т.е. абсолютно точное совпадение: .

Для линейной регрессии определяется коэффициент регрессии по формуле:

или .

Тогда

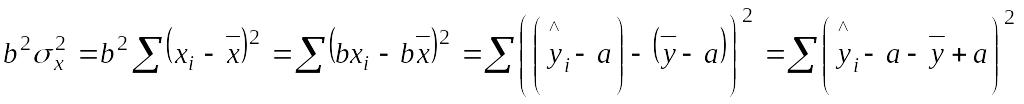- получившаяся формула есть дисперсия объясненная, факторная, тогда ;

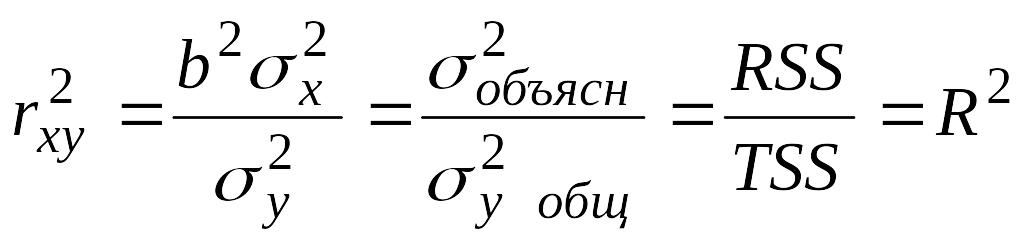отсюда, можно построить коэффициент (индекс корреляции ) для нелинейной регрессии

.

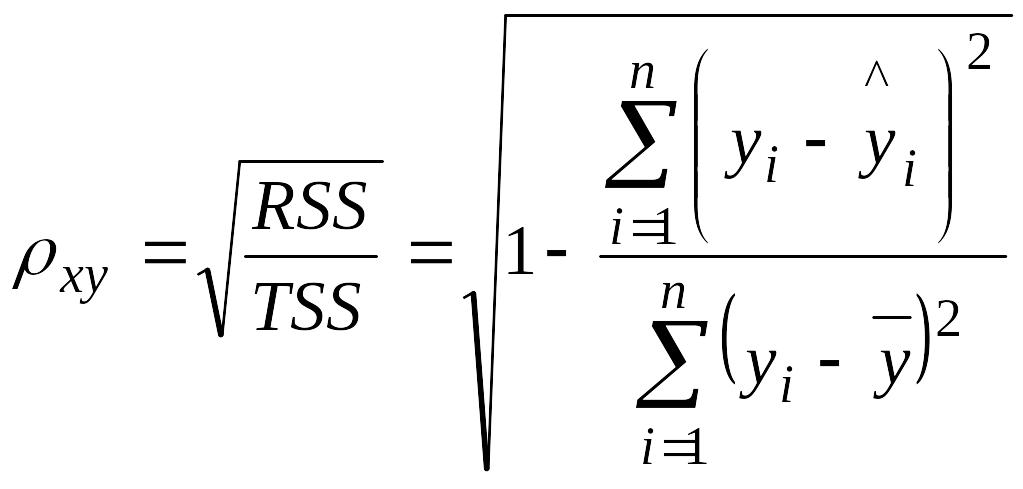Т.к. формулы для связи TSS, RSS, ESS мы получили в предположении что , то при , полученная формула не будет справедливой.

Использование F-критерия

С помощью F-критерия можно оценить качество построенной функции.

Поскольку при заданном объеме наблюдений ( , ) факторная сумма квадратов при линейной регрессии зависит только от одной константы - коэффициента регрессии , то говорят, что данная сумма квадратов имеет одну степень свободы.

К этому же выводу мы придем формальным путем, а именно, . Но свободный член , тогда

при заданном наборе переменных и , расчетное значение является в линейной регрессии функцией только одного параметра . Соответственно факторная сумма квадратов отклонений имеет число степеней свободы равное 1.

Любая сумма квадратов отклонений связана с числом степеней свободы, т.е. с числом свободы независимого варьирования признака. Значит число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показывать, сколько независимых отклонений из возможных требуется для образования данной суммы квадратов. Так для общей суммы квадратов требуется независимое отклонение, ибо по совокупности из единиц после расчета среднего уровня , свободно варьируют лишь числом отклонений.

Например, имеем ряд 1, 2, 3, 4, 5. Среднее =3, тогда n отклонений от среднего: -2, -1, 0, 1, 2. Т.к. то свободно варьируют 4 отклонения, а пятое может быть определено, если 4 известны.

Число степеней свободы в левой и правой частях соотношения (*) должно совпадать, то число степеней свободы второго слагаемого должно быть равно (n - 2).

То есть .

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что тоже самое, дисперсию на одну степень свободы D

.

Это приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточные дисперсии в расчете на одну степень свободы, получим величину F - отношения (F- критерия):

, где F- критерий для проверки нулевой гипотезы : .

Если нулевая гипотеза справедлива, то и не отличаются друг от друга. Для необходимо опровержение, то есть, чтобы факторная дисперсия превышала остаточную в несколько раз.

- это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности.

F-критерий - это оценивание качества уравнения регрессии, которое состоит в проверке гипотезы о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого производится сравнение фактического и значений F критерия Фишера-Снедекора. определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы

.

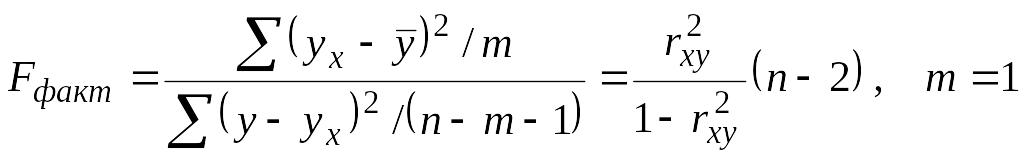- это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости . Уровень значимости - это вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно .

Если < , то - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

Если > , то - гипотеза не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

№ 7. Оценка соответствия уравнения регрессии исходным данным на основе средней ошибки аппроксимации.

Средняя ошибка аппроксимации оценивает, на сколько в среднем % расчётные значения результативного признака отклоняются от фактических в уравнении регрессии. Она позволяет судить о качестве модели и о подборе модели к исходным данным. Для её нахождения используется формулы:

1) 2)

где отклонения ( ) – абсолютная ошибка аппроксимации,

а отклонения относительная ошибка аппроксимации.

Значение и допустимый предел ошибки аппроксимации (5-7%). Среднее отклонение расчётных значений от фактических в числовом значении позволяет говорить о хорошем (не хорошем) качестве уравнения регрессии.

9. Оценка статистической значимости параметров эконометрической модели на основе критерия Стьюдетна.

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Требование нормальности распределения данных является необходимым для точного -теста. Однако, даже при других распределениях данных возможно использование -статистики. Во многих случаях эта статистика асимптотически имеет стандартное нормальное распределение — , поэтому можно использовать квантили этого распределения. Однако, часто даже в этом случае используют квантили не стандартного нормального распределения, а соответствующего распределения Стьюдента, как в точном -тесте. Асимптотически они эквивалентны, однако на малых выборках доверительные интервалы распределения Стьюдента шире и надежнее.

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

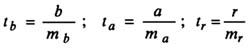
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

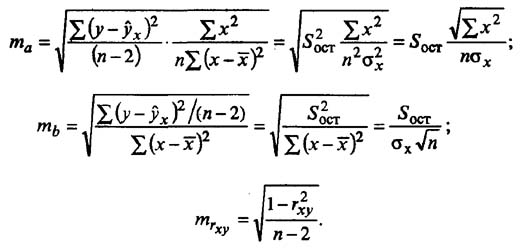
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

10. Точечный и интервальный прогнозы для модели парной регрессии

Точечный прогноз результативной переменной у на основе линейной модели парной регрессии при заданном значении факторной переменной хm будет осуществляться по формуле:

ym=

ym

t – t-критерий Стьюдента, который определяется в зависимости от заданного уровня значимости a и числа степеней свободы (n-2) для линейной модели парной регрессии;

Для линейной модели парной регрессии величина ошибки прогноза определяется по формуле:

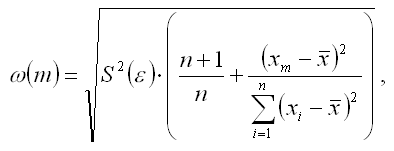
Предположим, что на основе выборочных данных была построена линейная модель парной регрессии вида:

Факторная переменная х в данной модели представлена в центрированном виде.

Задача состоит в расчёте прогноза результативной переменной у при заданном значении факторной переменной хm, т. е.

Математическое ожидание результативной переменной у в точке m рассчитывается по формуле:

Дисперсия результативной переменной у в точке m рассчитывается по формуле:

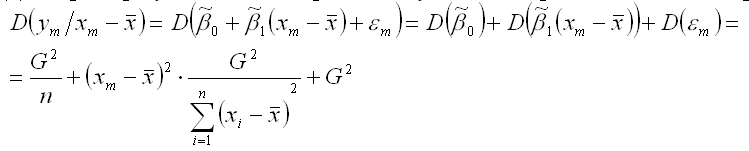
Следовательно, точечная оценка прогноза результативной переменной у в точке m имеет нормальный закон распределения с математическим ожиданием

и дисперсией

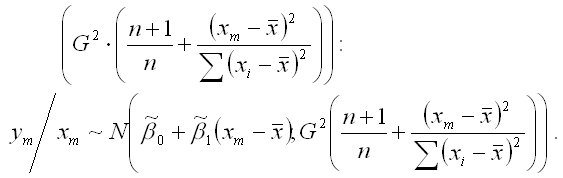
Если в формулу дисперсии результативной переменной у в точке m вместо дисперсии G2 подставить её выборочную оценку S2, то получим доверительный интервал для прогноза результативной переменной у при заданном значении факторной переменной хm:

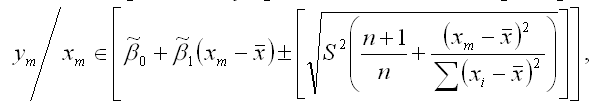
где выборочная оценка генеральной дисперсии S2 для линейной модели парной регрессии рассчитывается по формуле:

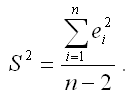
В этом случае прогнозный интервал можно преобразовать к виду:

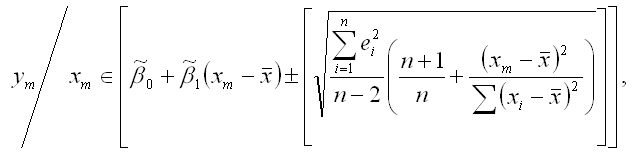
что и требовалось доказать.

12. Корреляция и регрессия нелинейных парных связей Простая регрессия – регрессия между двумя переменными – у и х, т.е. модели вида у= f(х) где у - зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная (признак - фактор). Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между явлениями. Практически в каждом отдельном случае величина у складывается из двух слагаемых: у_i=у_xi+ε_i где у_i – фактическое значение результативного признака; у_xi – теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т.е. из уравнения регрессии; ε_i – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных. В парной регрессии выбор вида математической функции у= f(х) может быть осуществлен тремя методами: 

• Графический метод – подбор вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции;

• Аналитический метод – основан на изучении материальной природы связи исследуемых признаков;

• Экспериментальный.

Нелинейная регрессия – если между экономическими явлениями существуют соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий:

• Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

• Регрессии, нелинейные по оцениваемым параметрам.

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

• Степенная;

• Показательная

• Экспоненциальная.

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция у=ах^bε. Связано это с тем что параметр b в ней имеет четкое экономическое истолкование, т.е. он является коэффициентом эластичности. Это означает, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Коэффициент детерминации – характеристика практической силы анализируемой регрессионной модели. Критерий Фишера (F) – показывает в какой мере регрессия лучше оценивает значение переменной по сравнению с ее средней.  13. Техника расчета и эконометрическая интерпретация параметров уравнения парной линейно регрессии, коэффициента парной линеной корреляции.

Парная регрессия представляет собой регрессию между двумя переменными

—у и х, т.е. модель вида , где y — результативный признак, т.е зависимая переменная; х - признак-фактор.

Уравнение линейной регрессии: ;

Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее пара­метров а и в.

; ; ;

Параметр b называется коэффициентом регрессии. Его вели­чина показываетсреднее изменение результата с изменением фактора на одну единицу.

Формально а — значение у при х = 0. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена, а не имеет смысла. Параметр, а может

не иметь экономического содержания.

Попытки экономически интерпретировать параметр, а могут привести к абсурду, особенно при а < 0. Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.