Задача Коши

Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, которое при заданном значении аргумента принимает заданное значение , т.е. удовлетворяет начальному условию .

Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через заданную точку . Решение задачи Коши называют частным решением дифференциального уравнения.

Пример. Найти:

• семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания;

• кривую этого семейства, проходящую через точку .

Решение.

Дифференциальное уравнение искомого семейства или .

Проинтегрировав обе части равенства, получим: , откуда ‑ уравнение семейства кривых, обладающих заданным свойством.

Определим значение , соответствующее начальным значениям: , т.е. .

Следовательно, ‑ искомая интегральная кривая.

Дифференциальное уравнение –го порядка можно свести к системе дифференциальных уравнений 1-го порядка. В самом деле, если обозначить через , через ,…, через , получим систему дифференциальных уравнений:

Для этой системы также можно ввести понятия частного и общего решений, а также начальных условий. Начальные условия можно задавать значениями всех функций в некоторой точке , т.е. это просто начальные условия исходного уравнения –го порядка. Когда такое решение будет найдено, то функция будет искомым частным решением исходного уравнения –го порядка. Верно и обратное: если дана произвольная система дифференциальных уравнений первого порядка, то, исключив из нее все неизвестные функции, кроме одной, ее можно свести к одному уравнению соответствующего порядка, которое, возможно, проще решить.

Пример. Решить систему двух уравнений первого порядка:

Решение. Продифференцировав первое уравнение, получим . Подставим в него из второго уравнения, получим . Общее решение этого уравнения имеет вид . Используя первое уравнение, получаем , и исходная система решена.

Теперь рассмотрим систему дифференциальных уравнений первого порядка вида:

,

которую коротко можно записать в векторной форме .

Задача Коши для такой системы формулируется следующим образом: для заданной точки найти вектор-функцию , которая является решением системы уравнений и .

Рассмотрим задачу Коши для разрешенного относительно дифференциального уравнения –го порядка , которое можно получить из рассмотренной выше системы дифференциальных уравнений первого порядка, если ввести обозначения:

;

;

;

;

……………………

;

,

получится эквивалентная система дифференциальных уравнений первого порядка:

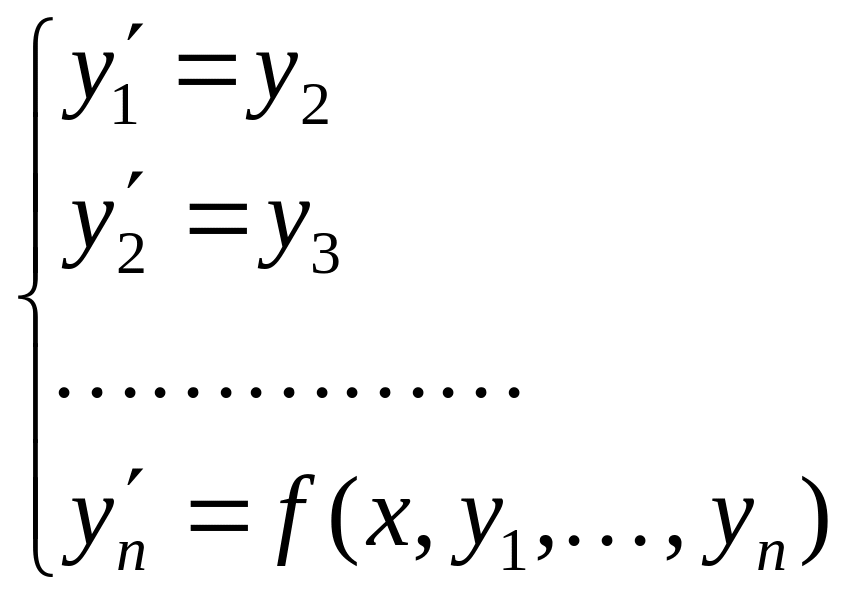
Задача Коши для уравнения –го порядка формулируется следующим образом: найти решение уравнения для данных значений:

Точки и называются начальными условиями, их можно записать также в виде и .

Существование и единственность решения задачи Коши может быть сформулировано в виде следующих теорем.

Теорема. Пусть в некоторой области функция и ее частная производная непрерывны. Тогда через каждую точку проходит единственное решение дифференциального уравнения .

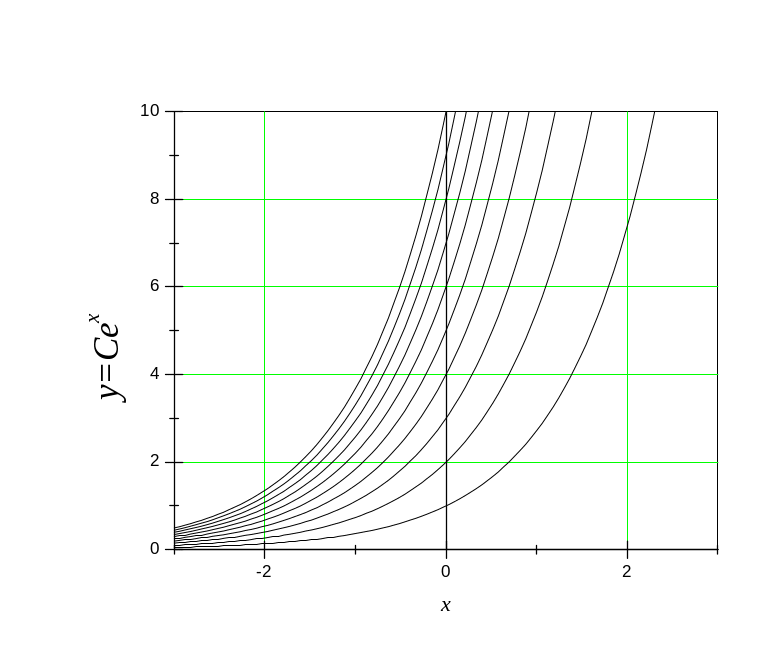
Графически это можно представить как семейство кривых, представляющих графики решений, которые полностью заполняют область , но при этом они не могут иметь общих точек, т.е. они не пересекаются и не касаются друг друга.

Теорема. Рассмотрим систему дифференциальных уравнений.

Если функции и их частные производные по непрерывны в –мерной области , то через каждую точку области проходит единственное в области решение системы дифференциальных уравнений:

Теоремы существования и единственности решения задачи Коши позволяют описать множество решений дифференциального уравнения в виде общего решения.