

Федеральное агентство по образованию Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Южно-Уральский государственный университет»
(национальный исследовательский университет)
Приборостроительный факультет
Кафедра «Электронно-вычислительные машины»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовой РАБОТЕ
по дисциплине «Математическая логика»
ЮУрГУ-230101. 2012.887 ПЗ КР
Руководитель:
/
 С.С. Ершов /
С.С. Ершов /
“______“ _____________ 2012г.
Автор работы:
студент группы ПС-226
/
 И.З. Гизитдинов /
И.З. Гизитдинов /
“______“ _____________ 2012г.
Работа защищена
“______“ _____________ 2012г.
С оценкой ___________________
Челябинск 2012
Федеральное агентство по образованию Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Южно-Уральский государственный университет»
(национальный исследовательский университет)
Приборостроительный факультет
Кафедра «Электронно-вычислительные машины»
Специальность «Вычислительные машины, комплексы, системы и сети»
УТВЕРЖДАЮ
Заведующий кафедрой
Кафтанников Игорь Леопольдович
_________________________ 2012г.
ЗАДАНИЕ
на курсовую работу студента
группы ПС-226, Гизитдинова Ильи Зуфаровича
1. Дисциплина «Математическая логика»
2. Перечень вопросов подлежащих разработке:
доказать справедливость схемы примитивной рекурсии для функции q(x,y) частного от целого деления y на x;
разработать программу уменьшения порядка постова слова на 1;
разработать программу копирования своей фамилии для машины Тьюринга.
Р уководитель
работы
/ С.С. Ершов /
уководитель
работы
/ С.С. Ершов /
А
 втор
работы
/ И.З. Гизитдинов /
втор
работы
/ И.З. Гизитдинов /
ОГЛАВЛЕНИЕ
1 СХЕМА ПРИМИТИВНОЙ РЕКУРСИИ ФУНКЦИИ q(x,y) ЧАСТНОГО ОТ ЦЕЛОГО ДЕЛЕНИЯ y НА x 5
2 РАЗРАБОТКА ПРОГРАММЫ ДЛЯ МАШИНЫ ПОСТА 7
2.1 Идея решения 7
2.2 Составление схем 7
2.3 Написание программы на машине Поста 11
2.4 Анализ результата 13
3 РАЗРАБОТКА ПРОГРАММЫ ДЛЯ МАШИНЫ ТЬЮРИНГА 14
3.1 Идея решения 14
3.2 Составление ГСП и ТСП 14
3.3 Написание программы на машине Тьюринга 15
3.4 Анализ результата 20
ВЫВОД 21
СПИСОК ЛИТЕРАТУРЫ 22
Введение
Основной целью студента, при освоении курса математической логики является получение основных фундаментальных знаний в этой области, необходимых для успешного понимания и освоения дисциплин, связанных с работой с информацией и электронно-вычислительными комплексами.
Цель данной работы – обобщение полученных знаний и навыков, применение их в практической деятельности. В частности решения следующих задач:
доказать справедливость схемы примитивной рекурсии для функции q(x,y) частного от целого деления y на x;
решение задачи проектирование программы уменьшения порядка постова слова на 1;
решение задачи проектирование программы копирования своей фамилии для машины Тьюринга.
Данная работа может быть использована для оценки понимания студентом основных принципов математической логики, принципиальных и функциональных особенностей машины Поста, Тьюринга, а также проектирование под данные машины и написание программ.
1 Схема примитивной рекурсии функции q(X,y) частного от целого деления y на X
Схему примитивной рекурсии для функции q(x,y) частного от целого деления y на x выглядит следующим образом:
![]() (1)
(1)
Функция q(x,y) примитивно рекурсивная, так как функции r(x,y), сложение, усечённая разность, sg(x) и отрицание являются примитивно рекурсивными.
Проверим данную схему рекурсии, будим вычислять значения q(x,y). Возьмём x=4 и y=14. (табл. 1)
Таблица 1 – Проверка ПР.
y |
y/x |
]y/x[ |
r(x,y) |
f=|x-(r(x,y)+1)| |
sg(f) |
⌐sg(f) |
q(x,y) |
Состояние |
0 |
0 |
0 |
_ |
_ |
_ |
_ |
0 |
- |
1 |
0,25 |
0 |
1 |
2 |
1 |
0 |
0 |
Сохранение значения |
2 |
0,5 |
0 |
2 |
1 |
1 |
0 |
0 |
Сохранение значения |
3 |
0,75 |
0 |
3 |
0 |
0 |
1 |
0 |
Сохранение значения |
4 |
1 |
1 |
0 |
3 |
1 |
0 |
1 |
Переход |
5 |
1,25 |
1 |
1 |
2 |
1 |
0 |
1 |
Сохранение значения |
6 |
1,5 |
1 |
2 |
1 |
1 |
0 |
1 |
Сохранение значения |
7 |
1,75 |
1 |
3 |
0 |
0 |
1 |
1 |
Сохранение значения |
8 |
2 |
2 |
0 |
3 |
1 |
0 |
2 |
Переход |
9 |
2,25 |
2 |
1 |
2 |
1 |
0 |
2 |
Сохранение значения |
10 |
2,5 |
2 |
2 |
1 |
1 |
0 |
2 |
Сохранение значения |
11 |
2,75 |
2 |
3 |
0 |
0 |
1 |
2 |
Сохранение значения |
12 |
3 |
3 |
0 |
3 |
1 |
0 |
3 |
Переход |
13 |
3,25 |
3 |
1 |
2 |
1 |
0 |
3 |
Сохранение значения |
14 |
3,5 |
3 |
2 |
1 |
1 |
0 |
3 |
Сохранение значения |
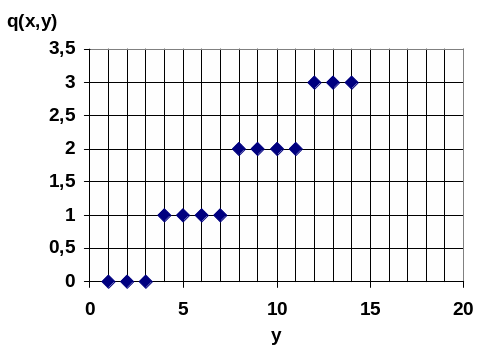
Рисунок 1 – графическое отображение ПРФ
Очевидно, что функция переходит в новое значение в точках, в которых y делится на x без остатка. (Рис.1)
