Основы систем класса MRP-MRPII

Геннадий Верников

Философия и основные понятия MRP В начале 60-х годов, в связи с ростом популярности вычислительных систем, возникла идея использовать их возможности для планирования деятельности предприятия, в том числе для планирования производственных процессов. Необходимость планирования обусловлена тем, что основная масса задержек в процессе производства связана с запаздыванием поступления отдельных комплектующих, в результате чего, как правило, параллельно с уменьшением эффективности производства, на складах возникает избыток материалов, поступивших в срок или ранее намеченного срока. Кроме того, вследствие нарушения баланса поставок комплектующих, возникают дополнительные осложнения с учетом и отслеживанием их состояния в процессе производства, т.е. фактически невозможно было определить, например, к какой партии принадлежит данный составляющий элемент в уже собранном готовом продукте. С целью предотвращения подобных проблем, была разработана методология планирования потребности в материалах MRP (Material Requirements Planning). Реализация системы, работающей по этой методологии представляет собой компьютерную программу, позволяющую оптимально регулировать поставки комплектующих в производственный процесс, контролируя запасы на складе и саму технологию производства. Главной задачей MRP является обеспечивание гарантии наличия необходимого количества требуемых материалов-комплектующих в любой момент времени в рамках срока планирования, наряду с возможным уменьшением постоянных запасов, а следовательно разгрузкой склада. Прежде чем описывать саму структуру MRP, следует ввести краткий глоссарий основных ее понятий:

• Материалами будем называть все сырье и отдельные комплектующие, составляющие конечный продукт. В дальнейшем мы не будем делать различий между понятиями "материал" и "комплектующий".

• MRP-система, MRP-программа -- компьютерная программа работающая по алгоритму, регламентированному MRP методологией. Как и любая компьютерная программа, обрабатывает файлы данных (входные элементы) и формирует на их основе файлы -результаты.

• Статус материала является основным указателем на текущее состояние материала. Каждый отдельный материал, в каждый момент времени, имеет статус в рамках MRP-системы, который определяет, имеется ли данный материал в наличии на складе, зарезервирован ли он для других целей, присутствует ли в текущих заказах, или заказ на него только планируется. Таким образом, статус материала однозначно описывает степень готовности каждого материала быть пущенным в производственный процесс.

• Страховой запас материала необходим для поддержания процесса производства в случае возникновения непредвиденных и неустранимых задержек в его поставках. По сути, в идеальном случае, если механизм поставок полагать безупречным, MRP-методология не постулирует обязательное наличие страхового запаса, и его объемы устанавливаются различными для каждого конкретного случая, в зависимости от сложившейся ситуации с поступлением материалов. Подробней об этом будет рассказано ниже.

• Потребность в материале в компьютерной MRP-программе представляет собой определенную количественную единицу, отображающую возникшую в некоторой момент времени в течение периода планирования необходимость в заказе данного материала. Различают понятия полной потребности в материале, которая отображает то количество, которое требуется пустить в производство, и чистой потребности, при вычислении которой учитывается наличие всех страховых и зарезервированных запасов данного материала. Заказ в системе автоматически создается по возникновению отличной от нуля чистой потребности.

Процесс планирования включает в себя функции автоматического создания проектов заказов на закупку и\или внутреннее производство необходимых материалов-комплектующих. Другими словами система MRP оптимизирует время поставки комплектующих, тем самым уменьшая затраты на производство и повышая его эффективность. Основными преимуществами использования подобной системе в производстве являются:

• Гарантия наличия требуемых комплектующих и уменьшение временных задержек в их доставке, и, следовательно, увеличение выпуска готовых изделий без увеличения числа рабочих мест и нагрузок на производственное оборудование.

• Уменьшение производственного брака в процессе сборки готовой продукции возникающего из-за использования неправильных комплектующих.

• Упорядовачивание производства, ввиду контроля статуса каждого материала, позволяющего однозначно отслеживать весь его конвейерный путь, начиная от создания заказа на данный материал, до его положения в уже собранном готовом изделии. Также благодаря этому достигается полная достоверность и эффективность производственного учета.

Все эти преимущества фактически вытекают из самой философии MRP, базирующейся на том принципе, что все материалы-комплектующие, составные части и блоки готового изделия должны поступать в производство одновременно, в запланированное время, чтобы обеспечить создание конечного продукта без дополнительных задержек. MRP-система ускоряет доставку тех материалов, которые в данный момент нужны в первую очередь и задерживает преждевременные поступления, таким образом, что все комплектующие, представляющие собой полный список составляющих конечного продукта поступают в производство одновременно. Это необходимо во избежание той ситуации, когда задерживается поставка одного из материалов, и производство вынуждено приостановиться даже при наличии всех остальных комплектующих конечного продукта. Основная цель MRP-системы формировать, контролировать и при необходимости изменять даты необходимого поступления заказов таким образом, чтобы все материалы, необходимые для производства поступали одновременно. В следующем разделе будут детально рассмотрены входные элементы MRP-программы и результаты ее работы.

Формирование входной информации для MRP-программы и результаты её работы На практике MRP-система представляет собой компьютерную программу, которая логически может быть представлена при помощи следующей диаграммы:

Диаграмма 1 Входные элементы и результаты работы MRP-программы На приведенной выше диаграмме отображены основные информационные элементы MRP-системы. Итак, опишем основные входные элементы MRP-системы:

• Описание состояния материалов (Inventory Status File) является основным входным элементом MRP-программы. В нем должна быть отражена максимально полная информация о всех материалах-комплектующих, необходимых для производства конечного продукта. В этом элементе должен быть указан статус каждого материала, определяющий, имеется ли он на руках, на складе, в текущих заказах или его заказ только планируется, а также описания, его запасов, расположения, цены, возможных задержек поставок, реквизитов поставщиков. Информация по всем вышеперечисленным позициям должна быть заложена отдельно по каждому материалу, участвующему в производственном процессе.

• Программа производства (Master Production Schedule) представляет собой оптимизированный график распределения времени для производства необходимой партии готовой продукции за планируемый период или диапазон периодов. Сначала создается пробная программа производства, впоследствии тестируемая на выполнимость дополнительно прогоном через CRP-систему (Capacity Requirements Planning), которая определяет достаточно ли производственных мощностей для ее осуществления. Если производственная программа признана выполнимой, то она автоматически формируется в основную и становится входным элементом MRP-системы. Это необходимо потому как рамки требований по производственным ресурсам являются прозрачными для MRP-системы, которая формирует на основе производственной программы график возникновения потребностей в материалах. Однако, в случае недоступности ряда материалов, или невозможности выполнить план заказов, необходимый для поддержания реализуемой с точки зрения CPR производственной программы, MRP-система в свою очередь указывает о необходимости внести в нее корректировки.

• Перечень составляющих конечного продукта (Bills of Material File) -- это список материалов и их количество, требуемое для производства конечного продукта. Таким образом, каждый конечный продукт имеет свой перечень составляющих. Кроме того, здесь содержится описание структуры конечного продукта, т.е. он содержит в себе полную информацию по технологии его сборки. Чрезвычайно важно поддерживать точность всех записей в этом элементе и соответственно корректировать их всякий раз при внесении изменений в структуру и\или технологию производства конечного продукта.

Напомним, что каждый из вышеуказанных входных элементов представляет собой компьютерный файл данных, использующийся MRP-программой. В настоящий момент MRP-системы реализованы на самых разнообразных аппаратных платформах и включены в качестве модулей в большинство финансово-экономических систем. Мы не будем останавливаться на техническом аспекте вопроса и перейдем к описанию логических шагов работы MRP-программы. Цикл ее работы состоит из следующих основных этапов:

1. Прежде всего MRP-система, анализируя принятую программу производства, определяет оптимальный график производства на планируемый период.

2. Далее, материалы, не включенные в производственную программу, но присутствующие в текущих заказах, включаются в планирование как отдельный пункт.

3. На этом шаге, на основе утвержденной программы производства и заказов на комплектующие, не входящие в нее, для каждого отдельно взятого материала вычисляется полная потребность, в соответствии с перечнем составляющих конечного продукта.

4. Далее, на основе полной потребности, учитывая текущий статус материала, для каждого периода времени и для каждого материала вычисляется чистая потребность, по указанной формуле. Если чистая потребность в материале больше нуля, то системой автоматически создается заказ на материал.

5. И наконец, все заказы созданные ранее текущего периода планирования, рассматриваются, и в них, при необходимости, вносятся изменения, чтобы предотвратить преждевременные поставки и задержки поставок от поставщиков.

Таким образом, в результате работы MRP-программы производится ряд изменений в имеющихся заказах и , при необходимости, создаются новые, для обеспечения оптимальной динамики хода производственного процесса. Эти изменения автоматически модифицируют Описание Состояния Материалов, так как создание, отмена или модификация заказа, соответственно влияет на статус материала, к которому он относится. В результате работы MRP-программы создается план заказов на каждый отдельный материал на весь срок планирования, обеспечение выполнения которого необходимо для поддержки программы производства. Основными результатами MRP-системы являются:

• План Заказов (Planned Order Schedule) определяет, какое количество каждого материала должно быть заказано в каждый рассматриваемый период времени в течение срока планирования. План заказов является руководством для дальнейшей работы с поставщиками и, в частности, определяет производственную программу для внутреннего производства комплектующих, при наличии такового.

• Изменения к плану заказов (Changes in planned orders) являются модификациями к ранее спланированным заказам. Ряд заказов могут быть отменены, изменены или задержаны, а также перенесены на другой период.

Также, MRP-система формирует некоторые второстепенные результаты, в виде отчетов, целью которых является обратить внимание на "узкие места" в течение планируемого периода, то есть те промежутки времени, когда требуется дополнительный контроль за текущими заказами, а также для того чтобы вовремя известить о возможных системных ошибках возникших при работе программы. Итак, MRP-система формирует следующие дополнительные результаты-отчеты:

• Отчет об "узких местах" планирования (Exception report) предназначен для того, чтобы заблаговременно проинформировать пользователя о промежутках времени в течение срока планирования, которые требуют особого внимания, и в которые может возникнуть необходимость внешнего управленческого вмешательства. Типичными примерами ситуаций, которые должны быть отражены в этом отчете могут быть непредвиденно запоздавшие заказы на комплектующие, избытки комплектующих на складах и т.п.

• Исполнительный отчет (Performance Report) является основным индикатором правильности работы MRP-системы и имеет целью оповещать пользователя о возникших критических ситуациях в процессе планирования, таких как, например, полное израсходование страховых запасов по отдельным комплектующим, а также о всех возникающих системных ошибках в процессе работы MRP-программы.

• Отчет о прогнозах (Planning Report) представляет собой информацию, используемую для составления прогнозов о возможном будущем изменении объемов и характеристик выпускаемой продукции, полученную в результате анализа текущего хода производственного процесса и отчетах о продажах. Также отчет о прогнозах может использоваться для долгосрочного планирования потребностей в материалах.

Таким образом, использование MRP-системы для планирования производственных потребностей позволяет оптимизировать время поступления каждого материала, тем самым значительно снижая складские издержки и облегчая ведения производственного учета. Однако, среди пользователей MRP-программ существует расхождение в мнениях относительно использования страхового запаса для каждого материала. Сторонники использования страхового запаса утверждают, что он необходим в силу того, что зачастую механизм доставки грузов не является достаточно надежным, и возникшее, в силу различных факторов, полное израсходование запасов на какой-либо материал, автоматически приводящее к остановке производства, обходится гораздо дороже, чем постоянно поддерживаемый его страховой запас. Противники использования страхового запаса утверждают, что его отсутствие является одной из центральных особенностей концепции MRP, поскольку MRP-система должна быть гибкой по отношению к внешним факторам, вовремя внося изменения к плану заказов, в случае непредвиденных и неустранимых задержек поставок. Но в реальной ситуации, как правило, вторая точка зрения может быть реализована для планирования потребностей для производства изделий, спрос на которые относительно прогнозируем и контролируем и объем производства может быть установлен в производственной программе постоянным в течение некоторого, относительно длительного периода. Следует заметить, что в Российских условиях, когда задержки в процессах поставки являются скорее правилом, чем исключением, на практике целесообразно применять планирование с учетом страхового запаса, объемы которого устанавливаются в каждом отдельном случае.

Планирование производственных мощностей с помощью CRP-cистемы (Capacity Requirements Planning) Система планирования производственных мощностей по методологии CRP применяется для проверки пробной программы производства, созданной в соответствии с прогнозами спроса на продукцию, на возможность ее осуществления имеющимися в наличии производственными мощностями. В процессе работы CRP-системы разрабатывается план распределения производственных мощностей для обработки каждого конкретного цикла производства в течение планируемого периода. Также устанавливается технологический план последовательности производственных процедур и, в соответствии с пробной программой производства, определяется степень загрузки каждой производственной единицы на срок планирования. Если после цикла работы CRP-модуля программа производства признается реально осуществимой, то она автоматически подтверждается и становится основной для MRP-системы. В противном случае в нее вносятся изменения, и она подвергается повторному тестированию с помощью CRP-модуля. В дальнейшем эволюционном развитии систем планирования производства они стали представлять собой интеграцию многих отдельных модулей, которые, взаимодействуя, увеличивали гибкость системы в целом. В следующем разделе будут описаны основные этапы дальнейшего развития систем класса MRP.

Эволюция MRP. Переход от MRP к MRPII

Системы планирования производства постоянно находятся в процессе эволюции. Первоначально MRP-системы фактически просто формировали на основе утвержденной производственной программы план заказов на определенный период, что не удовлетворяло вполне возрастающие потребности.

С целью увеличить эффективность планирования, в конце 70-х годов Оливер Уайт и Джордж Плосл предложили идею воспроизведения замкнутого цикла (closed loop) в MRP-системах. Идея заключалась в предложении ввести в рассмотрение более широкий спектр факторов при проведении планирования, путем введения дополнительных функций. К базовым функциям планирования производственных мощностей и планирования потребностей в материалах было предложено добавить ряд дополнительных, таких как контроль соответствия количества произведенной продукции количеству использованных в процессе сборки комплектующих, составление регулярных отчетов о задержках заказов, об объемах и динамике продаж продукции, о поставщиках и т.д. Термин "замкнутый цикл" отражает основную особенность модифицированной системы, заключающуюся в том, что созданные в процессе ее работы отчеты анализируются и учитываются на дальнейших этапах планирования, изменяя, при необходимости программу производства, а следовательно и план заказов. Другими словами, дополнительные функции осуществляют обратную связь в системе, обеспечивающую гибкость планирования по отношению к внешним факторам, таким как уровень спроса, состояние дел у поставщиков и т.п.

В дальнейшем, усовершенствование системы привело к трансформации системы MRP с замкнутым циклом в расширенную модификацию, которую впоследствии назвали MRPII (Manufactory Resource Planning), ввиду идентичности аббревиатур. Эта система была создана для эффективного планирования всех ресурсов производственного предприятия, в том числе финансовых и кадровых. Кроме того, система класса MRRPII способна адаптироваться к изменениям внешней ситуации и эмулировать ответ на вопрос "Что если". MRPII представляет собой интеграцию большого количества отдельных модулей, таких как планирование бизнес-процессов, планирование потребностей в материалах, планирование производственных мощностей, планирование финансов, управление инвестициями и т.д. Результаты работы каждого из модуля анализируются всей системой в целом, что собственно и обеспечивает ее гибкость по отношению к внешним факторам. Именно это свойство является краеугольным камнем современных систем планирования, поскольку большое количество производителей производят продукцию с заведомо коротким жизненным циклом, требующую регулярных доработок. В таком случае появляется необходимость в автоматизированной системе, которая позволяет оптимизировать объемы и характеристики выпускаемой продукции, анализируя текущий спрос и положение на рынке в целом.

В последние годы системы планирования класса MRPII в интеграции с модулем финансового планирования FRP (Finance Requirements Planning) получили название систем бизнес-планирования ERP (Enterprise Requirements Planning), которые позволяют наиболее эффективно планировать всю коммерческую деятельность современного предприятия, в том числе финансовые затраты на проекты обновления оборудования и инвестиции в производство новой линейки изделий. В Российской практике, целесообразность применения систем подобного класса обуславливается, кроме того, необходимостью управлять бизнес процессами в условиях инфляции, а также жесткого налогового прессинга, поэтому, системы ERP необходимы не только для крупных предприятий, но и для небольших фирм, ведущих активный бизнес. На следующей диаграмме представлена логическая схема системы планирования ресурсов производственного предприятия:

Диаграмма 2. Логическая структура системы планирования ресурсов производственного предприятия.

Для той сферы деятельности, которую мы называем «управление», можно сформулировать, похоже, совсем немного законов, действующих всеобщим образом и не зависящих от конкретных условий, объектов и времени.

Речь не идет о широко распространенных эмпирических правилах из серии «Х способов достичь результата Y» («7 признаков успешных людей», «3 способа мотивировать подчиненных», «5 правил ведения переговоров»  и т.п.) Это практичные советы, в той или иной мере эффективные в конкретной культурной среде и в некоторый период времени, предполагаемых их автором. Речь идет о совсем других законах, действующих на субъекты управленческой деятельности в той же мере, как и на другие объекты природы.

Есть основания к первому среди равных отнести закон о необходимом разнообразии, похоже, впервые явно сформулированным замечательным английским ученым Уильямом Росс Эшби (William Ross Ashby). В оригинальной формулировке он звучит невзрачно: «Разнообразие исходов [ситуации], если оно минимально, может быть еще более уменьшено лишь за счет соответствующего увеличения разнообразия, которым располагает регулятор». За этой внешней простотой содержится поистине великое открытие, имеющее принципиально важное значение для исследования возможностей управления, причем не абстрактно, а в вполне конкретных жизненных ситуациях. Цитата выше взята мной из книги «Введение в кибернетику» (1956 г.), глава 11.*    Стоит ознакомиться с оригинальным текстом автора, потому что способ, которым Уильям Росс Эшби пользуется для объяснений и доказательств не менее интересен, чем сама тема. В оригинальной трактовке используется термин регулирование (regulation), но управление (control) следует из него. Дело в том, что область действия этого закона распространяется на «технические» системы в равной мере как на управление коллективами людей и процессами человеческой деятельности.

Из этого закона непосредственно следует, что желательно иметь разнообразие возможных действий управляющего не ниже разнообразия вероятных действий управляемой им системы. Только в этом случае возможен надежный контроль исходов возникающих ситуаций. **

На бытовом уровне этот закон «знает» каждый. Чтобы научится управлять бытовой техникой, нужно понять назначение кнопок. Кнопки и различные сочетания их нажатий в свою очередь должны быть уникальны для однозначного выбора функций. Чем более «кнопок» управления имеет руководитель – тем лучше он может воспользоваться своим положением, своей ответственностью. Но есть более интересные следствия закона о необходимом разнообразии.

Рассмотрим игру двух соперников, где каждый находится примерно в равной ситуации и по очереди делает ходы, зависящие от результата ходов своего оппонента. Пусть это будут шахматы. Игрок, который способен лучше просчитывать результаты действий и который лучше знает похожие ситуации по своему прошлому опыту, практически управляет (в данном случае точнее сказать предопределяет) действиями другой стороны. Этот пример интересен тем, что несмотря на казалось бы почти равные возможности исходной ситуации и правила игры, один игрок имеет явное преимущество и, несомненно, воспользуется им. Разнообразие его действительных возможностей определено его лучшей организацией, лучшей возможностью понимания ситуации.

Законы и принципы кибернетики, применяемые в управлении организациями

       Для выяснения сущности управления и для рассмотрения проблем его организации и эффективности важное значение имеет установление связи между теорией управления и кибернетикой.

       Слово "кибернетика"^* возникло в Древней Греции. Впервые его произнес задолго до нашей эры философ Платон, произведя его от греческого слова "кибернус", что означало "кормчий". Вот почему древнее искусство управлять кораблем может служить первым символом кибернетики.

       В середине ХХ века новый смысл в это понятие вложил математик Н. Винер. Кибернетика - наука об управлении сложными динамическими системами и процессами. Объектом изучения этой науки являются системы любой природы, способные воспринимать, хранить и перерабатывать информацию и использовать её для управления и регулирования. Система^* (с греческого: составленное из частей, соединение) является одним из основных понятий кибернетики.

       Появление кибернетики - науки об общих закономерностях в процессах управления, осуществляемых в живых существах, машинах и их комплексах, - позволило собрать и обобщить огромное количество фактов, которые показали, что процесс управления во всех организованных системах сходен. Различие в управлении объектами касаются критериев цели, задач и содержания управления. Однако структура и построение процессов управления в организованных системах любых рангов имеют черты глубокого сходства, общности. Это обстоятельство объясняется тем, что процесс управления всегда представляет собой информационный процесс.

       Кибернетика изучает процессы получения и передачи, накопления и преобразования, переработки и использования информации в машинах, живых организмах и их объединениях. Установление связи между управлением и информационными процессами - важнейшее достижение кибернетики. Оно позволяет понять технологию процесса управления и, главное, подвергнуть его изучению количественными методами. Отличительная черта кибернетического подхода к познанию и совершенствованию процессов управления - использование их аналогов в живой и неживой природе и моделирование. Основная задача кибернетики - достижение на основе присущих ей методов и средств оптимального уровня управления, т. е. принятие наилучших управленческих решений. Таким образом, кибернетическим называется такое управление, которое:

• рассматривает организацию как некоторую большую систему, каждый элемент которой берется не только сам по себе, но и как часть большой совокупности, в которую он входит;

• обеспечивает оптимальное решение многовариантных динамических задач организации;

• использует специфические методы, выдвинутые кибернетикой (обратную связь, саморегулирование и самоорганизацию и т. п. );

• широко применяет механизацию и автоматизацию управленческих работ на основе использования вычислительной и управляющей техники и компьютерных технологий.

       Благодаря такой трактовке кибернетика^* находит практическое применение в самых различных областях деятельности человека, в том числе и в экономической. Ее приложение к экономике получило наименование экономической кибернетики, которая рассматривается как "использование научных подходов, основного комплекса понятий и научных инструментов кибернетики для исследования экономических явлений и решения практических экономических задач.

       Из кибернетики управление заимствует следующие законы и принципы необходимого разнообразия, эмерджентности^*, внешнего дополнения, обратной связи, выбора решения, декомпозиции, а также иерархии управления и автоматического регулирования (саморегулирования). Рассмотрим указанные законы и принципы с точки зрения их связи с вопросами управления организацией.

       Закон необходимого разнообразия. По определению У. Р. Эшби, первый фундаментальный закон кибернетики заключается в том, что разнообразие сложной системы требует управления, которое само обладает некоторым разнообразием. Иначе говоря, значительное разнообразие воздействующих на большую и сложную систему возмущений требует адекватного им разнообразия её возможных состояний. Если же такая адекватность в системе отсутствует, то это является следствием нарушения принципа целостности составляющих её частей (подсистем), а именно - недостаточного разнообразия элементов в организационном построении (структуре) частей.

       Ограничение разнообразия в поведении управляемого объекта достигается только за счет увеличения разнообразия органа управления (управленческих команд). Чтобы достигнуть минимума разнообразия выходных реакций (результатов деятельности) системы, управляющий орган должен быть способен к выработке определенного минимума команд и сигналов. Если его мощность ниже минимума, он не способен обеспечить полное управление.

       Процесс управления в конечном счете сводится к уменьшению разнообразия состояний управляемой системы, к уменьшению её неопределенности. В соответствии с этим законом, с увеличением сложности управляемой системы сложность управляемого блока также должна повышаться. Поэтому все большее усложнение аппарата управления корпорациями, холдингами, финансово-промышленными группами, и т. п. организациями и их частями в современных условиях - это закономерный процесс. Другое дело, что восполнять разнообразие управляющей системы нужно за счет внедрения компьютерных и других прогрессивных технологий управления и математических методов, а не за счет привлечения дополнительных людских ресурсов.

       Закон необходимого разнообразия^* имеет принципиальное значение для разработки оптимальной структуры системы управления. Если центральный орган управления при сохранении разумных размеров не обладает необходимым разнообразием, то следует развивать иерархическую структуру, передавая принятие определенных решений на нижние уровни и не допуская, чтобы они превращались в передаточные инстанции. Неудовлетворительные результаты проводимой в стране экономической реформы объясняются неадекватной реакцией органов управления. В стране увеличивается разнообразие форм собственности, разновидностей структурных формирований объектов управления, моделей хозяйствования и т. п. В соответствии с этими изменениями необходимо систему управления таким развитием привести в соответствие с законом необходимого разнообразия (обеспечить льготное кредитование структурных преобразований, разумное налогообложение развивающихся предприятий, государственную политику подготовки и переподготовки кадров и т. п. ).

       С позиции теории управления главнейшим моментом, характеризующим сложность системы, является её разнообразие. Поэтому определение степени оптимального разнообразия при разработке любых систем - организации производства, планирования, обслуживания, оперативного управления, систем оплаты труда и т. д. - является одним из наиболее важных и первоочередных этапов использования кибернетики при проектировании и функционировании организации.

       Этот вывод хорошо подтверждает и народная мудрость: "Ум хорошо, а два лучше", "Один в поле не воин". Заболевание организма человека очень часто связано с отсутствием необходимого и достаточного разнообразия в рационе питания, режиме работы и отдыха. Таким образом, соблюдение закона необходимого и достаточного разнообразия в проектировании и функционировании организационных систем повышает их эффективность и наоборот.

       Принцип эмерджентности. Второй принцип У. Э. Эшби, выражает следующее важное свойство сложной системы: "Чем больше система и чем больше различия в размерах между частью и целым, тем выше вероятность того, что свойства целого могут сильно отличаться от свойств частей". Указанные различия возникают в результате объединения в структуре системы (частей) определенного числа однородных или разнородных частей (элементов). Этот принцип указывает на возможность несовпадения локальных целей (частных целей отдельных элементов системы) с глобальной (общей) целью системы, а отсюда - на необходимость для достижения глобальных результатов принимать решения и вести разработки по совершенствованию системы и её частей на основе не только анализа, но и синтеза. Так, например, при построении дерева целей необходимо помнить о том, что система будет более эффективно функционировать в том случае, если достижение частных целей (например, работников фирмы) способствует достижению глобального (общего) оптимума системы (фирмы в целом).

       Принцип эмерджентности^* имеет большое значение для оптимизации системы управления. Он определяет требования системного подхода в решении проблем управления.

       Принцип внешнего дополнения. Впервые сформулированный С. Т. Биром третий принцип кибернетики гласит: любая система управления нуждается в "черном ящике" - определенных резервах, с помощью которых компенсируются неучтенные воздействия внешней и внутренней среды. Степень реализации этого принципа и определяет качество функционирования управляющей подсистемы. Действительно, в любом, даже самом детальном и тщательно разработанном плане нельзя учесть все многочисленные факторы, воздействующие на управляемую подсистему в процессе его реализации. Например, это может проявляться в недостаточной разработке каких-либо плановых показателей, в неполном учете при планировании и управлении всех факторов развития того или иного производства, в недостаточно качественном уровне информации, циркулирующей в системе, и т. п.

       Неучтенные факторы могут резко снизить надежность функционирования систем. Для удержания системы в заданных пороговых значениях переменных (показателей) необходимо наделить её нормативным уровнем резервов (стратегических, тактических, оперативных, технических, технологических, организационных, экономических и управленческих), компенсирующих воздействие этих факторов. Так, например, при проектировании участка и линий группового производства необходимо стремиться к загрузке оборудования на уровне, близком к нормативному его значению - 85%. Недогрузка 15% является тем резервом, который позволяет компенсировать неучтенные факторы: неотработанность конструкции, несовершенство технологии, недостаточный уровень квалификации рабочих и т. п.

       Закон обратной связи. Четвертый принцип кибернетики возведен в ранг фундаментального закона, который известен как закон обратной связи. Без наличия обратной связи между взаимосвязанными и взаимодействующими элементами, частями или системами невозможна организация эффективного управления ими на научных принципах. Все организованные системы являются открытыми, и замкнутость их обеспечивается только через контур прямой и обратной связи. Необходимым условием их эффективного функционирования является наличие обратной связи, сигнализирующей о достигнутом результате. На основании этой информации корректируется управляющее воздействие. В упрощенном виде это показано на рис. 1. 5. Входная величина r действует на управляемый процесс и в соответствии с передаточной функцией, характерной для данного объекта и определяющей соотношение между входными и выходными сигналами, превращаются в выходную величину с.

Рис. 1. 5 Схема управления с обратной связью (простая замкнутая система)

       Эта величина с помощью канала обратной связи подается на вход, корректирует входную величину r и в виде управляющего сигнала m воздействует, но уже по-новому, на объект. Возникшая таким образом связь образует замкнутый контур.

       Различают два вида обратной связи: отрицательную, которая уменьшает влияние входной величины на выходную величину, т. е. стремится как бы установить и поддержать некоторое устойчивое динамическое равновесие, и положительную, увеличивающую это влияние и тем самым создающую неустойчивое равновесие. Аналогичные регулирующие процессы происходят в биологических и социально-экономических системах. Таким образом, первая важная роль обратной связи - восстановление нормальной работы, нарушенной внешними и внутренними факторами, т. е. способность систем к саморегулированию и самоорганизации (адаптации). Создание самонастраивающихся и самообучающихся систем управления производством - одно из наиболее перспективных приложений кибернетики.

       Экономические системы находятся под постоянным воздействием природных и общественных факторов. Эти внешние воздействия, как правило, носят случайный характер. Вместе с тем сложность и изменчивость системы во времени приводят к тому, что поведение самой системы является в той или иной степени неопределенным, вероятностным. Влияние этих многочисленных неопределенностей приводит к тому, что экономические системы всегда являются системами с неполной информацией и управление ими всегда осуществляется в условиях неопределенности. Поэтому вторая важная роль обратной связи состоит в том, что, сообщая органу управления информацию о реальном состоянии объекта, она позволяет осуществлять регулирование в условиях неполной информации о возмущающих воздействиях.

       С кибернетической точки зрения обратная связь - процесс информационный. Воздействие входного сигнала на объект, переработка его в выходной сигнал и обратное действие выхода через канал обратной связи на входную величину - все это процессы передачи и переработки информации.

       Простейшим примером применения обратной связи на предприятии является диспетчерское управление: поступление на пульт диспетчера оперативных сведений о состоянии производства для выработки команд управления есть обратная связь по отношению к изменению объекта управления, рассматриваемому как сумма информации о нем.

       Закон обратной связи^* подчеркивает, что управление немыслимо без наличия как прямой, так и обратной связи между объектом и субъектом управления, образующими замкнутый контур. Применительно к планированию этот закон утверждает единство плана и отчета. Кто порождает план, тот организует учет, анализ и контроль его исполнения объектом управления.

       Принцип выбора решения. Пятый принцип кибернетики заключается в том, что решение должно приниматься на основе выбора одного из нескольких вариантов. Там, где принятие решения^* строится на анализе одного варианта, имеется субъективное управление. Разработка же многовариантных реакций в ответ на конкретную ситуацию, привлечение коллективного разума для разработки вариантов решений, в том числе с использованием метода "мозговой атаки", безусловно обеспечит принятие оптимального решения для конкретного случая. Этот принцип учитывает взаимосвязанность и обусловленность количественных и качественных изменений.

       Принцип декомпозиции. Этот принцип указывает на то, что управляемый объект всегда можно рассматривать как состоящий из относительно независимых друг от друга подсистем (частей). Данное положение, развитое У. Э. Эшби и Г. Клаусом, представляет значительный интерес для приложения кибернетики к производству. Дело в том, что приспособление регулятора к сложному объекту, учитывая все его аспекты и переменные, является теоретически и практически невозможным, так как на это никогда не хватило бы времени. Расчленение объекта на независимые звенья и переменные и самого регулятора на отдельные управляющие блоки обеспечивает возможность приспособления ко многим условиям и последовательного управления ими. Например, на практике диспетчер предприятия не рассматривает одновременно все возникшие возмущения. Он ранжирует их по степени влияния на производственный процесс^* и принимает меры к последовательному их устранению. Искусство управления заключается в отборе взаимосвязанных факторов, в расчленении решаемой задачи на ряд последовательных звеньев.

       Принципы иерархии управления и автоматического регулирования. Под иерархией понимается многоуровневое управление, характерное для всех организованных систем. Обычно нижние ярусы управления отличаются высокой скоростью реакции, быстротой переработки поступивших сигналов. На этом уровне происходит оперативное принятие решения^*. Например, при поломке инструмента рабочий быстро отключает станок от электросети.

       Чем менее разнообразны сигналы, тем быстрее реакция - ответ на информацию. По мере повышения уровня иерархии действия становятся более медленными, но отличаются большим разнообразием. Осуществляются они уже не в темпе воздействия, а могут включать в себя анализ, сопоставление, разработку различных вариантов реакции (ответ на информацию).

       Применительно к производству управление на уровне мастера участка должно быть быстрым, но предусматривать ответы лишь на простейшие ситуации. Управление^* на уровне цеха должно быть уже более медленным, так как оно включает в себя уже учет многих факторов и планирование на более длительное время. Отсюда следует необходимость обеспечить максимальную децентрализацию - саморегулирование и самоорганизацию системы без подключения более высоких уровней управления.

       Все указанные законы и принципы кибернетики взаимосвязаны и взаимообусловлены. Они должны непременно учитываться при организации структуры как объекта, так и субъекта управления, а в равной мере при реализации временного аспекта их организации, т. е. при осуществлении процессов планирования и управления.

       Рассмотренные принципы кибернетики последовательно связаны жесткой логикой и образуют замкнутый контур (рис. 1.7).

Основные методологии обследования организаций. Стандарт IDEF0. Геннадий Верников Научитесь видеть и понимать функциональную структуру своего бизнеса! В настоящее время в России резко возрос интерес к общепринятым на Западе стандартам менеджмента, однако, в реальной практике управления существует один очень показательный момент. Многих руководителей до сих пор можно поставить в тупик прямым вопросом об организационной структуре компании или о схеме существующих бизнес-процессов. Наиболее продвинутые и регулярно читающие экономическую периодику менеджеры, как правило, начинают чертить понятные только им одним иерархические диаграммы, но и в этом процессе обычно быстро заходят в тупик. То же самое касается сотрудников и руководителей различных служб и функциональных подразделений. В большинстве случаев, единственным набором изложенных правил, в соответствии с которыми должно функционировать предприятие, является набор отдельных положений и должностных инструкций. Чаще всего эти документы составлялись не один год назад, слабо структурированы и невзаимосвязаны между собой и, вследствие этого, просто пылятся на полках. До поры до времени подобный подход был оправдан, так как во время становления российской рыночной экономики понятие конкуренции практически отсутствовало, да и затраты считать не было особой необходимости - прибыль была гигантской. В результате этого, мы видим в течение последних двух лет вполне объяснимую картину: крупные компании, выросшие в начале 90-х годов, постепенно сдают свои позиции, вплоть до полного ухода с рынка. Отчасти это обусловлено тем, что на предприятии не были внедрены стандарты управления, полностью отсутствовало понятие функциональной модели деятельности и миссии. С помощью моделирования различных областей деятельности можно достаточно эффективно анализировать "узкие места" в управлении и оптимизировать общую схему бизнеса. Но, как известно, на любом предприятии высший приоритет имеют только те проекты, которые непосредственно приносят прибыль, поэтому речь об обследовании деятельности и ее реорганизации обычно идет только во время ощутимого кризиса в управлении компанией. В конце 90-ых годов, когда на рынке в должной мере появилась конкуренция и рентабельность деятельности предприятий стала резко падать, руководители ощутили огромные сложности при попытках оптимизировать затраты, чтобы продукция оставалась одновременно и прибыльной и конкурентоспособной. Как раз в этот момент совершенно четко проявилась необходимость иметь перед своими глазами модель деятельности предприятия, которая отражала бы все механизмы и принципы взаимосвязи различных подсистем в рамках одного бизнеса. Само же понятие "моделирование бизнес-процессов" пришло в быт большинства аналитиков одновременно с появлением на рынке сложных программных продуктов, предназначенных для комплексной автоматизации управления предприятием. Подобные системы всегда подразумевают проведение глубокого предпроектного обследования деятельности компании. Результатом этого обследование является экспертное заключение, в котором отдельными пунктами выносятся рекомендации по устранению "узких мест" в управлении деятельностью. На основании этого заключения, непосредственно перед проектом внедрения системы автоматизации, проводится так называемая реорганизация бизнес-процессов, иногда достаточно серьезная и болезненная для компании. Это и естественно, сложившийся годами коллектив всегда сложно заставить "думать по-новому". Подобные комплексные обследования предприятий всегда являются сложными и существенно отличающимися от случая к случаю задачами. Для решения подобных задач моделирования сложных систем существуют хорошо обкатанные методологии и стандарты. К таким стандартам относятся методологии семейства IDEF. С их помощью можно эффективно отображать и анализировать модели деятельности широкого спектра сложных систем в различных разрезах. При этом широта и глубина обследования процессов в системе определяется самим разработчиком, что позволяет не перегружать создаваемую модель излишними данными. В настоящий момент к семейству IDEF можно отнести следующие стандарты: IDEF0 - методология функционального моделирования. С помощью наглядного графического языка IDEF0, изучаемая система предстает перед разработчиками и аналитиками в виде набора взаимосвязанных функций (функциональных блоков - в терминах IDEF0). Как правило, моделирование средствами IDEF0 является первым этапом изучения любой системы; IDEF1 – методология моделирования информационных потоков внутри системы, позволяющая отображать и анализировать их структуру и взаимосвязи; IDEF1X (IDEF1 Extended) – методология построения реляционных структур. IDEF1X относится к типу методологий “Сущность-взаимосвязь” (ER – Entity-Relationship) и, как правило, используется для моделирования реляционных баз данных, имеющих отношение к рассматриваемой системе; IDEF2 – методология динамического моделирования развития систем. В связи с весьма серьезными сложностями анализа динамических систем от этого стандарта практически отказались, и его развитие приостановилось на самом начальном этапе. Однако в настоящее время присутствуют алгоритмы и их компьютерные реализации, позволяющие превращать набор статических диаграмм IDEF0 в динамические модели, построенные на базе “раскрашенных сетей Петри” (CPN – Color Petri Nets); IDEF3 – методология документирования процессов, происходящих в системе, которая используется, например, при исследовании технологических процессов на предприятиях. С помощью IDEF3 описываются сценарий и последовательность операций для каждого процесса. IDEF3 имеет прямую взаимосвязь с методологией IDEF0 – каждая функция (функциональный блок) может быть представлена в виде отдельного процесса средствами IDEF3; IDEF4 – методология построения объектно-ориентированных систем. Средства IDEF4 позволяют наглядно отображать структуру объектов и заложенные принципы их взаимодействия, тем самым позволяя анализировать и оптимизировать сложные объектно-ориентированные системы; IDEF5 – методология онтологического исследования сложных систем. С помощью методологии IDEF5 онтология системы может быть описана при помощи определенного словаря терминов и правил, на основании которых могут быть сформированы достоверные утверждения о состоянии рассматриваемой системы в некоторый момент времени. На основе этих утверждений формируются выводы о дальнейшем развитии системы и производится её оптимизация. В рамках этой статьи мы рассмотрим наиболее часто используемую методологию функционального моделирования IDEF0. История возникновения стандарта IDEF0 Методологию IDEF0 можно считать следующим этапом развития хорошо известного графического языка описания функциональных систем SADT (Structured Analysis and Design Teqnique). Несколько лет назад в России небольшим тиражом вышла одноименная книга, посвящанная описанию основных принципов построения SADT-диаграмм. Исторически, IDEF0, как стандарт был разработан в 1981 году в рамках обширной программы автоматизации промышленных предприятий, которая носила обозначение ICAM (Integrated Computer Aided Manufacturing) и была предложена департаментом Военно-Воздушных Сил США. Собственно семейство стандартов IDEF унаследовало свое обозначение от названия этой программы (IDEF=ICAM DEFinition). В процессе практической реализации, участники программы ICAM столкнулись с необходимостью разработки новых методов анализа процессов взаимодействия в промышленных системах. При этом кроме усовершенствованного набора функций для описания бизнес-процессов, одним из требований к новому стандарту было наличие эффективной методологии взаимодействия в рамках “аналитик-специалист”. Другими словами, новый метод должен был обеспечить групповую работу над созданием модели, с непосредственным участием всех аналитиков и специалистов, занятых в рамках проекта. В результате поиска соответствующих решений родилась методология функционального моделирования IDEF0. C 1981 года стандарт IDEF0 претерпел несколько незначительных изменения, в основном ограничивающего характера, и последняя его редакция была выпущена в декабре 1993 года Национальным Институтом По Стандарам и Технологиям США (NIST). Основные элементы и понятия IDEF0 Графический язык IDEF0 удивительно прост и гармоничен. В основе методологии лежат четыре основных понятия: Первым из них является понятие функционального блока (Activity Box). Функциональный блок графически изображается в виде прямоугольника (см. рис. 1) и олицетворяет собой некоторую конкретную функцию в рамках рассматриваемой системы. По требованиям стандарта название каждого функционального блока должно быть сформулировано в глагольном наклонении (например, “производить услуги”, а не “производство услуг”). Каждая из четырех сторон функционального блока имеет своё определенное значение (роль), при этом: Верхняя сторона имеет значение “Управление” (Control); Левая сторона имеет значение “Вход” (Input); Правая сторона имеет значение “Выход” (Output); Нижняя сторона имеет значение “Механизм” (Mechanism). Каждый функциональный блок в рамках единой рассматриваемой системы должен иметь свой уникальный идентификационный номер. Рисунок 1. Функциональный блок. Вторым “китом” методологии IDEF0 является понятие интерфейсной дуги (Arrow). Также интерфейсные дуги часто называют потоками или стрелками. Интерфейсная дуга отображает элемент системы, который обрабатывается функциональным блоком или оказывает иное влияние на функцию, отображенную данным функциональным блоком. Графическим отображением интерфейсной дуги является однонаправленная стрелка. Каждая интерфейсная дуга должна иметь свое уникальное наименование (Arrow Label). По требованию стандарта, наименование должно быть оборотом существительного. С помощью интерфейсных дуг отображают различные объекты, в той или иной степени определяющие процессы, происходящие в системе. Такими объектами могут быть элементы реального мира (детали, вагоны, сотрудники и т.д.) или потоки данных и информации (документы, данные, инструкции и т.д.). В зависимости от того, к какой из сторон подходит данная интерфейсная дуга, она носит название “входящей”, “исходящей” или “управляющей”. Кроме того, “источником” (началом) и “приемником” (концом) каждой функциональной дуги могут быть только функциональные блоки, при этом “источником” может быть только выходная сторона блока, а “приемником” любая из трех оставшихся. Необходимо отметить, что любой функциональный блок по требованиям стандарта должен иметь по крайней мере одну управляющую интерфейсную дугу и одну исходящую. Это и понятно – каждый процесс должен происходить по каким-то правилам (отображаемым управляющей дугой) и должен выдавать некоторый результат (выходящая дуга), иначе его рассмотрение не имеет никакого смысла. При построении IDEF0 – диаграмм важно правильно отделять входящие интерфейсные дуги от управляющих, что часто бывает непросто. К примеру, на рисунке 2 изображен функциональный блок “Обработать заготовку”. В реальном процессе рабочему, производящему обработку, выдают заготовку и технологические указания по обработке (или правила техники безопасности при работе со станком). Ошибочно может показаться, что и заготовка и документ с технологическими указаниями являются входящими объектами, однако это не так. На самом деле в этом процессе заготовка обрабатывается по правилам отраженным в технологических указаниях, которые должны соответственно изображаться управляющей интерфейсной дугой. Рисунок 2. Другое дело, когда технологические указания обрабатываются главным технологом и в них вносятся изменения (рис. 3). В этом случае они отображаются уже входящей интерфейсной дугой, а управляющим объектом являются, например, новые промышленные стандарты, исходя из которых производятся данные изменения. Рисунок 3. Приведенные выше примеры подчеркивают внешне схожую природу входящих и управляющих интерфейсных дуг, однако для систем одного класса всегда есть определенные разграничения. Например, в случае рассмотрения предприятий и организаций существуют пять основных видов объектов: материальные потоки (детали, товары, сырье и т.д.), финансовые потоки (наличные и безналичные, инвестиции и т.д.), потоки документов (коммерческие, финансовые и организационные документы), потоки информации (информация, данные о намерениях, устные распоряжения и т.д.) и ресурсы (сотрудники, станки, машины и т.д.). При этом в различных случаях входящими и исходящими интерфейсными дугами могут отображаться все виды объектов, управляющими только относящиеся к потокам документов и информации, а дугами-механизмами только ресурсы. Обязательное наличие управляющих интерфейсных дуг является одним из главных отличий стандарта IDEF0 от других методологий классов DFD (Data Flow Diagram) и WFD (Work Flow Diagram). Третьим основным понятием стандарта IDEF0 является декомпозиция (Decomposition). Принцип декомпозиции применяется при разбиении сложного процесса на составляющие его функции. При этом уровень детализации процесса определяется непосредственно разработчиком модели. Декомпозиция позволяет постепенно и структурированно представлять модель системы в виде иерархической структуры отдельных диаграмм, что делает ее менее перегруженной и легко усваиваемой. Модель IDEF0 всегда начинается с представления системы как единого целого – одного функционального блока с интерфейсными дугами, простирающимися за пределы рассматриваемой области. Такая диаграмма с одним функциональным блоком называется контекстной диаграммой, и обозначается идентификатором “А-0”. В пояснительном тексте к контекстной диаграмме должна быть указана цель (Purpose) построения диаграммы в виде краткого описания и зафиксирована точка зрения (Viewpoint). Определение и формализация цели разработки IDEF0 – модели является крайне важным моментом. Фактически цель определяет соответствующие области в исследуемой системе, на которых необходимо фокусироваться в первую очередь. Например, если мы моделируем деятельность предприятия с целью построения в дальнейшем на базе этой модели информационной системы, то эта модель будет существенно отличаться от той, которую бы мы разрабатывали для того же самого предприятия, но уже с целью оптимизации логистических цепочек. Точка зрения определяет основное направление развития модели и уровень необходимой детализации. Четкое фиксирование точки зрения позволяет разгрузить модель, отказавшись от детализации и исследования отдельных элементов, не являющихся необходимыми, исходя из выбранной точки зрения на систему. Например, функциональные модели одного и того же предприятия с точек зрения главного технолога и финансового директора будут существенно различаться по направленности их детализации. Это связано с тем, что в конечном итоге, финансового директора не интересуют аспекты обработки сырья на производственных станках, а главному технологу ни к чему прорисованные схемы финансовых потоков. Правильный выбор точки зрения существенно сокращает временные затраты на построение конечной модели. В процессе декомпозиции, функциональный блок, который в контекстной диаграмме отображает систему как единое целое, подвергается детализации на другой диаграмме. Получившаяся диаграмма второго уровня содержит функциональные блоки, отображающие главные подфункции функционального блока контекстной диаграммы и называется дочерней (Child diagram) по отношению к нему (каждый из функциональных блоков, принадлежащих дочерней диаграмме соответственно называется дочерним блоком – Child Box). В свою очередь, функциональный блок - предок называется родительским блоком по отношению к дочерней диаграмме (Parent Box), а диаграмма, к которой он принадлежит – родительской диаграммой (Parent Diagram). Каждая из подфункций дочерней диаграммы может быть далее детализирована путем аналогичной декомпозиции соответствующего ей функционального блока. Важно отметить, что в каждом случае декомпозиции функционального блока все интерфейсные дуги, входящие в данный блок, или исходящие из него фиксируются на дочерней диаграмме. Этим достигается структурная целостность IDEF0 – модели. Наглядно принцип декомпозиции представлен на рисунке 4. Следует обратить внимание на взаимосвязь нумерации функциональных блоков и диаграмм - каждый блок имеет свой уникальный порядковый номер на диаграмме (цифра в правом нижнем углу прямоугольника), а обозначение под правым углом указывает на номер дочерней для этого блока диаграммы. Отсутствие этого обозначения говорит о том, что декомпозиции для данного блока не существует. Часто бывают случаи, когда отдельные интерфейсные дуги не имеет смысла продолжать рассматривать в дочерних диаграммах ниже какого-то определенного уровня в иерархии, или наоборот - отдельные дуги не имеют практического смысла выше какого-то уровня. Например, интерфейсную дугу, изображающую “деталь” на входе в функциональный блок “Обработать на токарном станке” не имеет смысла отражать на диаграммах более высоких уровней – это будет только перегружать диаграммы и делать их сложными для восприятия. С другой стороны, случается необходимость избавиться от отдельных “концептуальных” интерфейсных дуг и не детализировать их глубже некоторого уровня. Для решения подобных задач в стандарте IDEF0 предусмотрено понятие туннелирования. Обозначение “туннеля” (Arrow Tunnel) в виде двух круглых скобок вокруг начала интерфейсной дуги обозначает, что эта дуга не была унаследована от функционального родительского блока и появилась (из “туннеля”) только на этой диаграмме. В свою очередь, такое же обозначение вокруг конца (стрелки) интерфейсной дуги в непосредственной близи от блока – приёмника означает тот факт, что в дочерней по отношению к этому блоку диаграмме эта дуга отображаться и рассматриваться не будет. Чаще всего бывает, что отдельные объекты и соответствующие им интерфейсные дуги не рассматриваются на некоторых промежуточных уровнях иерархии – в таком случае, они сначала “погружаются в туннель”, а затем, при необходимости “возвращаются из туннеля”. Последним из понятий IDEF0 является глоссарий (Glossary). Для каждого из элементов IDEF0: диаграмм, функциональных блоков, интерфейсных дуг существующий стандарт подразумевает создание и поддержание набора соответствующих определений, ключевых слов, повествовательных изложений и т.д., которые характеризуют объект, отображенный данным элементом. Этот набор называется глоссарием и является описанием сущности данного элемента. Например, для управляющей интерфейсной дуги “распоряжение об оплате” глоссарий может содержать перечень полей соответствующего дуге документа, необходимый набор виз и т.д. Глоссарий гармонично дополняет наглядный графический язык, снабжая диаграммы необходимой дополнительной информацией. Рисунок 4. Декомпозиция функциональных блоков. Принципы ограничения сложности IDEF0-диаграмм Обычно IDEF0-модели несут в себе сложную и концентрированную информацию, и для того, чтобы ограничить их перегруженность и сделать удобочитаемыми, в соответствующем стандарте приняты соответствующие ограничения сложности: Ограничение количества функциональных блоков на диаграмме тремя-шестью. Верхний предел (шесть) заставляет разработчика использовать иерархии при описании сложных предметов, а нижний предел (три) гарантирует, что на соответствующей диаграмме достаточно деталей, чтобы оправдать ее создание; Ограничение количества подходящих к одному функциональному блоку (выходящих из одного функционального блока) интерфейсных дуг четырьмя. Разумеется, строго следовать этим ограничениям вовсе необязательно, однако, как показывает опыт, они являются весьма практичными в реальной работе. Дисциплина групповой работы над разработкой IDEF0-модели Стандарт IDEF0 содержит набор процедур, позволяющих разрабатывать и согласовывать модель большой группой людей, принадлежащих к разным областям деятельности моделируемой системы. Обычно процесс разработки является итеративным и состоит из следующих условных этапов: Создание модели группой специалистов, относящихся к различным сферам деятельности предприятия. Эта группа в терминах IDEF0 называется авторами (Authors). Построение первоначальной модели является динамическим процессом, в течение которого авторы опрашивают компетентных лиц о структуре различных процессов. На основе имеющихся положений, документов и результатов опросов создается черновик (Model Draft) модели. Распространение черновика для рассмотрения, согласований и комментариев. На этой стадии происходит обсуждение черновика модели с широким спектром компетентных лиц (в терминах IDEF0- читателей) на предприятии. При этом каждая из диаграмм черновой модели письменно критикуется и комментируется, а затем передается автору. Автор, в свою очередь, также письменно соглашается с критикой или отвергает её с изложением логики принятия решения и вновь возвращает откорректированный черновик для дальнейшего рассмотрения. Этот цикл продолжается до тех пор, пока авторы и читатели не придут к единому мнению. Официальное утверждение модели. Утверждение согласованной модели происходит руководителем рабочей группы в том случае, если у авторов модели и читателей отсутствуют разногласия по поводу ее адекватности. Окончательная модель представляет собой согласованное представление о предприятии (системе) с заданной точки зрения и для заданной цели. Наглядность графического языка IDEF0 делает модель вполне читаемой и для лиц, которые не принимали участия в проекте ее создания, а также эффективной для проведения показов и презентаций. В дальнейшем, на базе построенной модели могут быть организованы новые проекты, нацеленные на производство изменений на предприятии (в системе). Особенности национальной практики применения функционального моделирования средствами IDEF0 В последние годы интерес в России к методологиям семейства IDEF неуклонно растет. Это я постоянно наблюдаю, просматривая статистику обращений к своей персональной web-странице (http://consulting.psi.ru), на которой кратко описаны основные принципы этих стандартов. При этом интерес к таким стандартам, как IDEF3-5 я бы назвал теоретическим, а к IDEF0 вполне практически обоснованным. Собственно говоря, первые Case-средства, позволяющие строить DFD и IDEF0 диаграммы появились на российком рынке еще в 1996 году, одновременно с выходом популярной книги по принципам моделирования в стандартах SADT. Тем не менее, большинство руководителей до сих пор расценивают практическое применение моделирования в стандартах IDEF скорее как дань моде, нежели чем эффективный путь оптимизации существующей системы управления бизнесом. Вероятнее всего это связано с ярко выраженным недостатком информации по практическому применению этих методологий и с непременным софтверным уклоном абсолютного большинства публикаций. Не секрет, что практически все проекты обследования и анализа финансовой и хозяйственной деятельности предприятий сейчас в России так или иначе связаны с построением автоматизированных систем управления. Благодаря этому, стандарты IDEF в понимании большинства стали условно неотделимы от внедрения информационных технологий, хотя с их помощью порой можно эффективно решать даже небольшие локальные задачи, буквально при помощи карандаша и бумаги. При проведении сложных проектов обследования предприятий, разработка моделей в стандарте IDEF0 позволяет наглядно и эффективно отобразить весь механизм деятельности предприятия в нужном разрезе. Однако самое главное – это возможность коллективной работы, которую предоставляет IDEF0. В моей практической деятельности было достаточно много случаев, когда построение модели осуществлялось с прямой помощью сотрудников различных подразделений. При этом, консультант за достаточно короткое время объяснял им основные принципы IDEF0 и обучал работе с соответствующим прикладным программным обеспечением. В результате, сотрудники различных отделов создавали IDEF-диаграммы деятельности своего функционального подразделения, которые должны были ответить на следующие вопросы: Что поступает в подразделение “на входе”? Какие функции, и в какой последовательности выполняются в рамках подразделения? Кто является ответственным за выполнение каждой из функций? Чем руководствуется исполнитель при выполнении каждой из функций? Что является результатом работы подразделения (на выходе)? После согласования черновиков диаграмм внутри каждого конкретного подразделения, они собираются консультантом в черновую модель предприятия, в которой увязываются все входные и выходные элементы. На этом этапе фиксируются все неувязки отдельных диаграмм и их спорные места. Далее, эта модель вновь проходит через функциональные отделы для дальнейшего согласования и внесения необходимых корректив. В результате, за достаточно короткое время и при привлечении минимума человеческих ресурсов со стороны консультационной компании (а эти ресурсы, как известно, весьма недешевы), получается IDEF0-модель предприятия по принципу “Как есть”, причем, что немаловажно, она представляет предприятие с позиции сотрудников, которые в нем работают и досконально знают все нюансы, в том числе неформальные. В дальнейшем, эта модель будет передана на анализ и обработку к бизнес-аналитикам, которые будут заниматься поиском “узких мест” в управлении компанией и оптимизацией основных процессов, трансформируя модель “Как есть” в соответствующее представление “Как должно быть”. На основании этих изменений и выносится итоговое заключение, которое содержит в себе рекомендации по реорганизации сисемы управления. Разумеется, подобный подход требует ряда организационных мер, в первую очередь со стороны руководства обследуемого предприятия. Это обусловлено тем, что эта техника подразумевает возложение на некоторых сотрудников дополнительных обязанностей по освоению и практическому применению новых методологий. Однако в конечном итоге это оправдывает себя, так как дополнительные один-два часа работы отдельных сотрудников в течение нескольких дней позволяют существенно экономить средства на оплату консультационных услуг сторонней компании (которые в любом случае будут отрывать от работы тех же работников анкетами и вопросами). Что касается самих работников предприятия, так или иначе выраженного противодействия с их стороны я в своей практике не встречал. Вывод из всего этого можно сделать следующий: совершенно не обязательно каждый раз самим придумывать решения для стандартных задач. Всегда, когда Вы сталкиваетесь с необходимостью анализа той или иной функциональной системы (от системы проектирования космического корабля, до процесса приготовления комплексного ужина) – используйте годами проверенные и обкатанные методы. Одним из таких методов и является IDEF0, позволяющий с помошью своего простого и понятного инструментария решать сложные жизненные задачи. Дата публикации: 08.02.2000

©

Проектное управление: модели и методы принятия решений

В конце 50-х годов в США для осуществления программы исследовательских и конструкторских работ по созданию ракеты “Поларис” впервые был использован метод планирования и управления, основанный на идее определения, оценки вероятных сроков и контроля так называемого “критического пути” всего комплекса работ. Результаты превзошли все ожидания: во-первых, заметно уменьшилось число сбоев в работе из-за несогласованности используемых ресурсов, резко сократилась общая продолжительность выполнения всего комплекса работ, получен огромный эффект из-за снижения суммарной потребности в ресурсах и, соответственно, уменьшения общей стоимости программы. Вскоре после того, как результаты выполнения программы “Поларис” стали достоянием общественности¹ , весь мир заговорил о методе PERT (Project Evaluation and Review Technique) как о новом подходе к организации управления.

За прошедшее с тех пор время метод “критического пути” не только получил широкое применение в повседневной практике управления, но и обусловил появление специальной научно-прикладной дисциплины – управление проектами. В центре внимания этой дисциплины находятся вопросы планирования, организации, контроля и регулирования хода выполнения проектов, организации материально-технического, финансового и кадрового обеспечения проектов, оценки инвестиционной привлекательности различных вариантов реализации проектов.

В современной деловой среде актуальность проектного управления как метода организации и управления производством значительно возросла. Это обусловлено объективными тенденциями в глобальной реструктуризации бизнеса. Принцип концентрации производственно-экономического потенциала уступил место принципу сосредоточения на развитии собственного потенциала организации. Крупные производственно-хозяйственные комплексы конгломеративного типа быстро замещаются гибкими сетевыми структурами, среди участников которых доминирует принцип предпочтения использования внешних ресурсов внутренним (outsourcing). Поэтому производственная деятельность всё больше превращается в комплекс работ со сложной структурой используемых ресурсов, сложной организационной топологией, сильной функциональной зависимостью от времени и огромной стоимостью.

Объект проектного управления

Термин проект, как известно, происходит от латинского слова projectus, что в буквальном переводе означает “брошенный вперед”. Таким образом, сразу становится ясно, объект управления, который можно представить в виде проекта, отличает возможность его перспективного развертывания, т.е. возможность предусмотреть его состояния в будущем. Хотя различные официальные источники трактуют понятие проекта по-разному2 , во всех определениях четко просматриваются особенности проекта как объекта управления, обусловленные комплексностью задач и работ, четкой ориентацией этого комплекса на достижение определенных целей и ограничениями по времени, бюджету, материальным и трудовым ресурсам.

Однако, любая деятельность, в том числе и та, которую никто не собирается называть проектом, выполняется в течение определенного периода времени и связана с затратами определенных финансовых, материальных и трудовых ресурсов. Кроме того, любая разумная деятельность, как правило, целесообразна, т.е. направлена на достижение определенного результата. И, тем не менее, в одних случаях к управлению деятельностью подходят как к управлению проектом, а в других случаях – нет.

Деятельность как объект управления рассматривается в виде проекта тогда, когда

• она объективно имеет комплексных характер и для ее эффективного управления важное значение имеет анализ внутренней структуры всего комплекса работ (операций, процедур и т.п.);

• переходы от одной работы к другой определяют основное содержание всей деятельности;

• достижение целей деятельности связано с последовательно-параллельным выполнением всех элементов этой деятельности;

• ограничения по времени, финансовым, материальным и трудовым ресурсам имеют особое значение в процессе выполнения комплекса работ;

• продолжительность и стоимость деятельности явно зависит от организации всего комплекса работ.

Поэтому, объектом проектного управления принято считать особым образом организованный комплекс работ, направленный на решение определенной задачи или достижение определенной цели, выполнение которого ограничено во времени, а также связано с потреблением конкретных финансовых, материальных и трудовых ресурсов. При этом под “работой” понимается элементарная, неделимая часть данного комплекса действий.

Элементарность работы – понятие условное и относительное. То, что нецелесообразно делить в одной системе действий, полезно разукрупнять в другой. Например, если за элемент комплекса работ по сборке автомобиля принимается технологическая операция, то одной из “работ” может считаться установка сборщиком фары. Эта “работа” в данном случае неделима, так как остаются неизменными ее факторы – исполнитель, предмет и объект действия. Но, как только мы начинаем рассматривать исполнение этой работы как отдельную задачу, она сама превращается в комплекс.

Однако если задача возникает регулярно, а ее решение превращается в рутинную деятельность, доведенную до автоматизма, то нет никакого особого смысла каждый раз, приступая к ее решению, рассматривать и моделировать ее сложную структуру. Результат известен заранее и время, потраченное на планирование, будет просто потеряно. Поэтому объектом проектного управления является, как правило, комплекс взаимосвязанных работ, направленных на решение некоторой оригинальной задачи. Но, в том то и дело, что в современной деловой среде, при стремительном развитии техники, технологии и организации производства, при стремительной смене видов и разновидностей товаров и услуг на рынках, появление перед менеджером оригинальных задач стало фактически обычной ситуацией. Если в конце пятидесятых годов, на заре зарождения проектного управления, в качестве объектов такого управления выступали исключительно научно-исследовательские и опытно-конструкторские программы, то в наши дни уже мало кого можно удивить техническими, организационными, экономическими и даже социальными проектами. Уже в самом определении типа проекта заложена характеристика области его приложения.

Теоретические основы проектного управления

Для описания, анализа и оптимизации проектов наиболее подходящими оказались сетевые модели, представляющие из себя разновидность ориентированных графов.

В сетевой модели роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае будут соответствовать работам. Такую сетевую модель принято называть сетевой моделью с работами на дугах (Activities on Arrows, AoA). В то же время, возможно, что в сетевой модели роль вершин графа играют работы, а дуги отображают соответствие между окончанием одной работы и началом другой. Такую сетевую модель принято называть сетевой моделью с работами в узлах (Activities on Nodes, AoN).

Пусть множество A={a1, a2, a3, ... an} – комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V={v1, v2, v3, ..., vm} будет представлять комплекс событий, возникающих в процессе выполнения комплекса работ, то сетевая модель будет задаваться ориентированным графом G=(V, A), в котором элементы множества V играют роль вершин, а элементы множества A – роль дуг, соединяющих вершины, причем каждой дуге ai можно поставить в однозначное соответствие пару вершин (vsi, vfi), первая из которых будет определять момент начала работы аi, а вторая – момент окончания этой работы. Такая сетевая модель будет сетевой моделью с работами на дугах.

Теперь пусть множество A={a1, a2, a3, ... an} – по-прежнему будет рассматриваться как комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V={v1, v2, v3, ..., vm} будет представлять комплекс отношений предшествования-следования работ в процессе их выполнения, то сетевая модель будет задаваться ориентированным графом G=(A, V), в котором элементы множества A играют роль вершин, а элементы множества V – роль дуг, соединяющих вершины, причем каждой дуге vi можно поставить в однозначное соответствие пару вершин (asi, afi), первая из которых будет непосредственно предшествующей работой в данной паре, а вторая – непосредственно следующей. Такая сетевая модель будет сетевой моделью с работами в узлах.

Сетевая модель может быть представлена: 1) сетевым графиком, 2) в табличной форме, 3) в матричной форме, 4) в форме диаграммы на шкале времени. Как будет показано ниже, переход от одной формы представления к другой не составляет большого труда.

Преимущество сетевых графиков и временных диаграмм перед табличной и матричной формами представления состоит в их наглядности. Однако это преимущество исчезает прямо пропорционально тому, как увеличиваются размеры сетевой модели. Для реальных задач сетевого моделирования, в которых речь идет о тысячах работ и событий, вычерчивание сетевых графиков и диаграмм теряет всякий смысл.

Преимущество табличной и матричной формы перед графическими представлениями состоит в том, что с их помощью удобно осуществлять анализ параметров сетевых моделей; в этих формах применимы алгоритмические процедуры анализа, выполнение которых не требует наглядного отображения модели на плоскости.

Сетевым графиком называется полное графическое отображение структуры сетевой модели на плоскости.

Если сетевым графиком на плоскости отображается сетевая модель типа АоА, то однозначное представление должны получить все работы и все события модели. Однако структура сетевого графика модели АоА может быть более избыточна, чем структура самой отображаемой сетевой модели. Дело в том, что по правилам построения сетевого графика для удобства его анализа необходимо, чтобы два события были соединены только единственной работой, что в принципе не соответствует реальным обстоятельствам в окружающей нас действительности. Поэтому принято вводить в структуру сетевого графика элемент, которого нет ни в действительности, ни в сетевой модели. Этот элемент называется фиктивной работой. Таким образом, структура сетевого графика образуется из трех типов элементов (в отличие от структуры сетевой модели, где только два типа элементов):

• событий – моментов времени, когда происходит начало или окончание выполнения какой-либо работы (работ);

• работ – неделимых частей комплекса действий, необходимых для решения некоторой задачи;

• фиктивных работ – условных элементов структуры сетевого графика, используемых исключительно для указания логической связи отдельных событий.

Графически события изображаются кружками, разделенными на три равных сегмента (радиусами под углом в 120°); работы изображаются сплошными линиями со стрелками на конце, ориентированными слева направо; фиктивные работы изображаются пунктирными линиями со стрелками на конце, ориентированными слева направо. Пример сетевого графика модели АоА представлен ниже на рис. 1.

Отметим, что индексация работ производится рядом с соответствующими стрелками; фиктивные работы не индексируются; индексы событий проставляются в нижнем сегменте соответствующего кружка. Заполнение остальных сегментов рассматривается ниже.

Если сетевым графиком отображается модель типа AoN, то избыточности структуры удается избежать. Здесь нет необходимости вводить в качестве дополнительного структурного элемента фиктивные работы, поскольку отсутствуют те структурные элементы, которые они призваны обслуживать, а именно – события. В сетевом графике модели типа AoN есть только узлы (или вершины), которые обозначают работы и дуги (сплошные линии со стрелками, ориентированными слева направо), которые обозначают отношения предшествования-следования работ. Никаких событий и никаких фиктивных работ! Заметим, что в наиболее известной программе по проектному управлению Microsoft Project реализуется именно этот тип модели.

Здесь узлы сети, соответствующие работам, принято изображать прямоугольниками, поделенными на 5 секторов. В центральном секторе проставляется индекс (или записывается наименование работы). Заполнение остальных секторов рассматривается ниже. Пример сетевого графика для модели типа AoN представлен ниже на рис. 2.

Рисунок 2. Пример сетевого графика модели типа АоN.

В табличной форме сетевая модель задается множеством {A, A(IP)}, где А – это множество индексов работ, а A(IP) множество комбинаций работ, непосредственно предшествующих работе А. Для рассматриваемого выше примера табличная форма сетевой модели будет такой, которая представлена в табл. 1.

Таблица 1. Табличная форма сетевой модели.

Матричная форма описания сетевой модели задается в виде отношения между событиями (ei, ej), которое равно 1, если между этими событиями есть работа (либо реальная, либо фиктивная) и 0 – в противном случае. Матричная форма для описания сетевой модели из рассматриваемого выше примера приведена ниже в табл. 2:

Таблица 2

События	1	2	3	4	5	6	7
1		1	1
2	1					1
3	1			1	1
4			1		1	1
5			1	1			1
6		1		1			1
7					1	1

Описание сетевой модели в форме временной диаграммы (или графика Ганта) предполагает размещение работ в координатной системе, где по оси абсцисс (X) откладывается время (t), а по оси ординат (Y) – работы. Точкой начала отсчета любой из работ будет момент окончания всех ее предшествующих работ. Если работе не предшествует ничто, то она откладывается от начала временной шкалы, т.е. с самого левого края диаграммы. На рис. 3 представлен график Ганта для сетевой модели по данным табл. 1 с добавлением информации о продолжительности выполнения работ.

Поскольку в сетевых графиках моделей типа АоА вершины соответствуют событиям, постольку эти элементы структуры обладают свойством “сшивания” предыдущих работ с последующими. Иными словами, любое событие наступает только тогда, когда закончены все предшествующие ему работы. С другой стороны, оно является предпосылкой для начала следующих за ним работ. Событие не имеет продолжительности и наступает мгновенно. В связи с этим предъявляются особые требования к его определению.

Так, каждое событие, включаемое в сетевой график, должно быть полно, четко и всесторонне определено, его формулировка должна включать результат всех непосредственно предшествующих ему работ. И пока не выполнены все работы, непосредственно предшествующие данному событию, не может наступить и само событие, а, следовательно, не может быть начата ни одна из работ, непосредственно следующих за ним. Более того, если то или иное событие наступило, то это означает, что могут быть немедленно и реально начаты работы, следующие за ним. Если же по какой-либо причине хотя бы одна из таких работ не может быть начата, следовательно, нельзя считать данное событие наступившим.

Рисунок 3

Различаются следующие разновидности событий сетевого графика модели АоА:

• исходное событие – результат, в отношении которого условно предполагается, что он не имеет предшествующих работ;

• завершающее событие – результат, в отношении которого предполагается, что за ним не следует ни одна работа; это и является конечной целью выполнения всего комплекса работ или решением задачи;

• промежуточное событие или просто событие. Это любой достигаемый результат в выполнении одной или нескольких работ, дающий возможность начать последующие работы;

• начальное событие – событие, непосредственно предшествующее данной конкретной работе;

• конечное событие – событие, непосредственно следующее за данной работой.

Временные параметры (или временные характеристики) сетевой модели являются главными элементами аналитической системы проектного управления. Именно для их определения и последующего улучшения выполняется вся подготовительная, вспомогательная работа по составлению сетевой модели проекта и ее последующей оптимизации.

Различают следующие временные параметры:

• продолжительность работ;

• раннее время начала работы;

• раннее время окончания работы;

• позднее время начала работы;

• позднее время окончания работы;

• раннее время наступления события;

• позднее время наступления события;

• продолжительность критического пути;

• резерв времени наступления события;

• полный резерв времени выполнения работы;

• свободный резерв времени выполнения работы;

• независимый резерв времени выполнения работы.

Продолжительность работы (ti) – календарное время, которое занимает выполнение работы.

Раннее время начала работы (ESTi) – наиболее ранний из возможных сроков начала выполнения работы.

Раннее время окончания работы (EFTi) – равно раннему времени начала работы плюс ее продолжительность.

Позднее время окончания работы (LFTi) – наиболее поздний из допустимых сроков окончания работы.

Позднее время начала работы (LSTi) – равно позднему времени окончания работы минус ее продолжительность.

Раннее время наступления события (EETj) – характеризует наиболее ранний из возможных сроков свершения того или иного события. Поскольку каждое событие является результатом свершения одной или нескольких работ, а те в свою очередь следуют за какими-либо предшествующими событиями, то срок его наступления определяется величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.

Позднее время наступления события (LETj) – характеризует наиболее поздний из допустимых сроков совершения того или иного события. Если установлен срок наступления завершающего события, являющегося результатом всего комплекса проводимых работ, то каждое промежуточное событие должно наступить не позже определенного срока. Этот срок и является предельно допускаемым сроком наступления события.

Любая последовательность непосредственно следующих друг за другом работ в сетевой модели называется путем. Путей в сетевой модели может быть очень много, но при этом пути, связывающие исходное и завершающее события сетевой модели, называются полными, а все остальные – неполными. Сумма продолжительностей выполнения работ, составляющих тот или иной путь, называется продолжительностью этого пути.

Самый продолжительный из всех полных путей называется критическим путем сетевой модели. Таким образом, продолжительность критического пути равна сумме продолжительностей всех работ, составляющих этот путь.

Работы, лежащие на критическом пути, называются критическими работами, а события – критическими событиями.

Уже одного определения критического пути сетевой модели проекта достаточно для организации управления всем комплексом работ. Жестко контролируя календарные сроки выполнения критических работ, можно в итоге избежать потерь. У работ, не находящихся на критическом пути, как правило, имеются резервы времени, позволяющие на некоторое время откладывать их выполнение, если это необходимо.

Резерв времени наступления события – это разница между поздним и ранним сроками наступления этого события.

Полный резерв времени выполнения работы (TFi) – это максимально возможный запас времени для выполнения данной работы сверх продолжительности самой работы при условии, что в результате такой задержки конечное для данной работы событие наступит не позднее, чем в свой поздний срок.

Свободный резерв времени выполнения работы (FFi) – это запас времени, которым можно располагать при выполнении данной работы в предположении, что предшествующее и последующее события этой работы наступают в свои самые ранние сроки.

Независимый резерв времени выполнения работы (IFi) – это запас времени, на который можно отложить начало выполнения работы без риска повлиять на какие бы то ни было сроки наступления каких-либо событий в модели вообще.

Параметры раннего и позднего времени наступления события используются в маркировке вершин сетевого графика модели типа АоА. В левый сегмент записывается раннее время наступления соответствующего события (ЕETj), а в правый – позднее (LETj), что показано на рис 4.

Рисунок 4. Пример маркировки времени наступления событий

В маркировке вершин сетевого графика модели типа AoN помимо индекса работ используются параметры (см. Рис. 5):

• раннего времени начала выполнения работы (ESTj), которое записывается в левый верхний сектор прямоугольника, маркирующего вершину работы;

• позднего времени начала выполнения работы (LSTj), которое записывается в правый верхний сектор прямоугольника, маркирующего вершину работы;

• продолжительность выполнения работы (tj), которая записывается в левый нижний сектор прямоугольника, маркирующего вершину работы;

• полный резерв времени выполнения работы (TFi) – который записывается в правый нижний сектор прямоугольника, маркирующего вершину работы.

Рисунок 5. Пример маркировки вершин сетевого графика модели типа АоN

Методы расчета временных параметров и критического пути сетевой модели проекта

Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.

Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.

В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.

Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров

Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:

• Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].

• Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].

• Раннее время окончания работы [ij]:

EFTij = ESTij + tij.

• Позднее время начала работы [ij]: LSTij = LFTij – tij.

• Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max { EFTrj, EFTnj, ..., EFTmj}, где [rj], [nj], ..., [mj] – индексы работ, для которых событие [j] является конечным.

• Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min { LSTjr, LSTjn, ..., LSTjm}, где [jr], [jn], ..., [jm] – индексы работ, для которых событие [j] является начальным.

• Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]

• Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.

• Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.

• Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.

• Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.

Рассмотрим сначала матричный метод определения временных параметров.

Прежде всего, необходимо составить квадратную матрицу (см. Рис. 7), число столбцов и строк, в которой равно числу событий сетевой модели. Строки и столбы индексируются в одинаковом порядке индексами события. Полученные на пересечении строк и столбцов клетки разбиваются на две части по диагонали снизу слева вверх вправо. Левая верхняя часть клетки называется ее числителем, правая нижняя – знаменателем.

Первый шаг заполнения матрицы заключается в следующем. Если события [i] и [j] соединяются какой-то работой, то продолжительность этой работы tij заносится в числители двух клеток: клетки, лежащей на пересечении i-й строки и j-го столбца, и клетки лежащей на пересечении j-й строки и i-го столбца. Эти действия выполняются для всех работ сетевой модели, а числители всех остальных клеток, кроме клеток, лежащих на главной (слева сверху вправо вниз) диагонали матрицы, заполняются нулями или вообще не заполняются.

Следующий шаг заполнения матрицы первоначально предполагает занесение в числитель первой клетки главной диагонали значения 0. Это равносильно тому, что мы полагаем, что раннее время наступления исходного события сетевой модели равно 0. Затем осуществляем заполнение знаменателей тех клеток первой строки, лежащих справа от (или над) главной диагонали, чьи числители содержат значения больше 0. При этом значения, которые проставляются в знаменатели, вычисляются как сумма числителя клетки данной строки, лежащей на главной диагонали, и числителя заполняемой клетки. Таким образом, мы подсчитываем раннее время окончания соответствующей работы. Результат выполнения этих действий приведен на рис. 8.

Рисунок 7. Разметка матрицы при определении временных параметров сетевой модели матричным методом

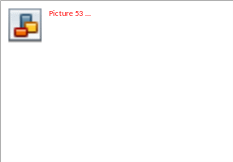
Рисунок 8.

Нетрудно проверить по формулам, что раннее время окончания работы 1-2 равно 4, а работы 1-4 равно 7.

Следующий шаг заполнения матрицы начинается с того, что мы должны решить, какое значение должно стоять в числителе диагональной клетки второй строки. По определению это должно быть значение, соответствующее раннему началу события 2. Раннее начало некоторого события, являющегося конечным для нескольких работ, равно моменту раннего окончания самой поздней из работ, которые заканчиваются данным событием. Значит, просто необходимо просмотреть знаменатели клеток столбца 2 сверху вниз до главной диагонали и выбрать максимальное значение, после чего записать его в числитель диагональной клетки 2. В нашем примере это будет знаменатель клетки 1-2, который равен 4.

После этого также, как были подсчитаны знаменатели в первой строке выше диагонали, подсчитываются знаменатели клеток второй строки выше диагонали.

Процедуры, описанные выше, повторяются до тех пор, пока не будет найден числитель последней диагональной клетки.

Дойдя до последней диагональной клетки (см. Рис. 9), мы получили значение раннего времени наступления завершающего события сетевой модели (36), которое и определяет продолжительность критического пути. Вместе с тем, для завершающего события, как известно, раннее время равно позднему времени его наступления, следовательно, знаменатель этой клетки будет равен ее числителю. Запишем это.

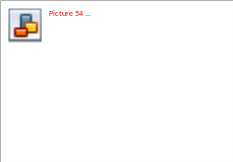
Рисунок 9

Получив значение знаменателя последней диагональной клетки, можно вычислить значения знаменателей клеток (чьи числители больше 0), находящихся в той же строке слева (ниже) от главной диагонали. Они будут равны разнице значения знаменателя соответствующей диагональной клетки и значения числителя клетки, для которой производится расчет. Так, например, значение знаменателя клетки 8-7 будет равно 36-5=31, а клетки 8-4 будет равно 36-6=30.

После подсчета всех знаменателей в последней строке можно найти значение знаменателя в диагональной клетке на предпоследней строке. Оно будет равно минимальному значению из знаменателей всех клеток, лежащих в данном столбце ниже главной диагонали, т.е. 31.

Затем аналогичным образом обсчитываем предпоследнюю строку и находим знаменатель третьей от конца диагональной клетки.

Из заполненной матрицы нетрудно увидеть не только продолжительность критического пути (числитель или знаменатель последней диагональной клетки), но также сам критический путь. Он проходит через события, у которых раннее и позднее время наступления равны, т.е. через события, у которых в соответствующих диагональных клетках совпадают числители и знаменатели. В нашем примере это будут события 1, 2, 4, 6, 8 (см. Рис. 9).

В соответствии с расчетными формулами резервов времени, которые были приведены выше, полный резерв времени выполнения работы, находящейся между событиями i и j, определяется разностью значений знаменателя диагональной клетки j-j и знаменателя клетки j в строке i выше главной диагонали. Чтобы найти свободный резерв времени выполнения работы, находящейся между событиями i и j, необходимо из числителя диагональной клетки j-j вычесть числитель диагональной клетки i-i и числитель клетки i-j. Чтобы найти независимый резерв времени выполнения работы, находящейся между событиями i и j, необходимо из числителя диагональной клетки j-j вычесть знаменатель диагональной клетки i-i и числитель клетки i-j.

Так, для работы 3-5 полный резерв будет равен 29-9=20, свободный – 17-2-7=8, а независимый – 17-22-7=-12 (принимается равным 0). Для работы 2-6 полный резерв будет равен 26-12=14, свободный – 26-4-8=14 и независимый – 26-4-8=14.

На рис. 10 приведены результаты расчетов всех резервов времени на основании данных из таблицы на рис. 9.

Табличный метод. Составляется таблица, число строк в которой равно числу работ, включающая в себя следующие столбцы (в порядке их следования слева направо):

1. индекс работы;

2. индексы непосредственно предшествующих работ;

3. индексы непосредственно следующих работ;

4. продолжительность выполнения работы;

5. раннее время начала выполнения работы;

6. позднее время начала выполнения работы;

7. раннее время окончания выполнения работы;

8. позднее время окончания выполнения работы;

9. полный резерв времени работы;

10. свободный резерв времени работы;

11. независимый резерв времени работы.

Исходная информация, связанная с описанием топологии сетевой модели, содержится в столбцах (1), (2) и (4). Суть табличного метода расчета временных параметров сетевой модели состоит в последовательном заполнении остальных столбцов данной таблицы.

Алгоритм табличного метода предусматривает выполнение следующих последовательных шагов.

Рисунок 10

ШАГ 1. Определение индексов непосредственно следующих работ.

Рассматриваем работу с индексом [i]. Непосредственно следующие за ней работы – это те работы, для которых работа [i] является непосредственно предшествующей. Следовательно, индексы непосредственно следующих работ – это индексы тех работ, у которых в столбце (2) содержится индекс работы [i].

ШАГ 2. Определение раннего времени начала и раннего времени окончания работ.

Определение раннего времени начала и раннего окончания работ, т.е. заполнение столбцов (5) и (7) таблицы должно осуществляться одновременно, т.к. время начала одних работ зависит от времени окончания других.

Заполнение указанных столбцов осуществляется последовательно от начала сетевой модели к ее концу, т.е. сверху вниз. При этом действуют следующие правила:

• Раннее время окончания рассматриваемой работы равно раннему времени ее начала (из столбца (5)) плюс продолжительность работы (из столбца (4)).

• Раннее время начала выполнения работы равно 0, если данной работе непосредственно не предшествует ни одна из работ сетевой модели, или равно максимальному раннему времени окончания среди всех непосредственно предшествующих ей работ (из столбца (7)).

Продолжительность критического пути равна максимальному значению в столбце (7).

ШАГ 3. Определение позднего времени окончания и позднего времени начала работ.

Определение позднего времени окончания и позднего начала работ, т.е. заполнение столбцов (6) и (8) таблицы должно осуществляться также одновременно, т.к. время начала одних работ зависит от времени окончания других.

Заполнение указанных столбцов осуществляется последовательно от конца сетевой модели к ее началу, т.е. снизу вверх. При этом действуют следующие правила:

• Позднее время начала рассматриваемой работы равно позднему времени ее окончания (из столбца (8)) минус продолжительность работы (из столбца (4)).

• Позднее время окончания выполнения работы равно продолжительности критического пути, если за данной работой нет ни одной непосредственно следующей работы (из столбца (3)) сетевой модели, или равно минимальному позднему времени начала среди всех непосредственно следующих за данной работой работ (из столбца (6)).

Шаг 4. Определение полного резерва времени выполнения работы.

Полный резерв времени работы [i] находится как разность значений ее позднего и раннего времени окончания (соответственно, столбцы (8) и (7)), либо как разность значений ее позднего и раннего начала выполнения (соответственно, столбцы (6) и (5)).

Шаг 5. Определение свободного резерва времени выполнения работы.

Свободный резерв времени работы [i] определяется как разность между значением раннего времени начала любой из непосредственно следующих за ней работ и суммой раннего времени начала работы [i] и ее продолжительности.

Шаг 6. Определение независимого резерва времени выполнения работы.

Независимый резерв времени работы [i] определяется как разность между значением раннего времени начала любой из непосредственно следующих за ней работ и суммой позднего времени наступления начального события работы [i] и ее продолжительности. Позднее время наступления начального события работы [i] табличным путем определяется как минимальное позднее время начала тех работ, у которых с работой [i] одинаковый состав непосредственно предшествующих работ.

По приведенным выше правилам заполнена следующая табл. 3.

Таблица 3.

Работа	Непосредс. Предшеств.	Непосредств Следующая.	t	EST	LST	EFT	LFT	TF	FF	IF
A	–	D, E	4	0	0	4	4	0	0	0
B	–	H, I, J	7	0	7	7	14	7	7	0
C	–	F, G	2	0	20	2	22	20	0	0
D	A	M	8	4	18	12	26	14	14	14
E	A	H, I, J	10	4	4	14	14	0	0	0
F	C	K, L	7	2	22	9	29	20	8	0
G	C	N	6	2	25	8	31	23	11	0
H	B, E	M	12	14	14	26	26	0	0	0
i	b, e	–	6	14	30	20	36	16	16	16
J	B, E	K, L	3	14	26	17	29	12	0	0
K	F, J	–	4	17	32	21	36	15	15	3
L	F, J	N	2	17	29	19	31	12	0	0
M	D, H	–	10	26	26	36	36	0	0	0
N	G, L	–	5	19	31	24	36	12	12	0

Основы сетевого моделирования в условиях неопределенности

На практике чаще всего допускают, что продолжительность работ, составляющих проект, определена достаточно четко. Преимущества такого подхода к сетевому моделированию комплексных задач вполне очевидны:

• благодаря такой сети получается полное и ясное представление относительно всего комплекса работ; четко выявляются связи всех элементов комплекса;

• выявление критического пути позволяет установить работы, определяющие ход выполнения всего комплекса (т.е. критические работы);

• появляется полная ясность относительно резервов времени, на которые можно откладывать выполнение отдельных работ, не находящихся на критическом пути, а это, в свою очередь, позволяет более эффективно распоряжаться наличными ресурсами.

Однако в реальной жизни очень часто приходится сталкиваться с ситуациями, когда продолжительность работ не может быть определена точно, а лишь приблизительно. Например, в научно-исследовательских проектах, связанных с проведением экспериментов, ученому заранее не известно, сколько потребуется сделать опытов для получения надежного искомого результата. В бизнесе при разработке программы инвестиций заранее неизвестно, сколько времени займет ее согласование в различных инстанциях. При строительстве дома тоже можно допустить ошибку в количестве дней, которые займет рытье котлована под фундамент, а ошибка может быть очень просто связана с недооценкой сложности грунта.

В принципе, могут иметь место два случая: 1) либо работы не являются новыми, и мы знаем приблизительно закон распределения продолжительности выполнения каждой их них, 2) либо эти работы совершенно новые для нас, и закон распределения продолжительности их выполнения нам неизвестен.

В первом случае, известность закона распределения продолжительности выполнения работы автоматически подразумевает известность таких двух его параметров как:

• математическое ожидание m продолжительности выполнения работы;

• дисперсия s2 продолжительности выполнения работы.

Во втором случае, когда точный закон распределения продолжительности выполнения работ неизвестен предполагается, что это распределение подчиняется нормальному закону и описывается b-функцией, которая имеет следующие математическое ожидание и дисперсию:

m = 1/6(O + 4M + P);

s2 =[1/6 (O – P)]2.

Таким образом, в любом случае для оценки продолжительности любой работы мы будем иметь его ожидаемое время (математическое ожидание) и погрешность (дисперсию) этого ожидания.

Процедура построения и разметки сетевого графика в случае со случайной продолжительностью работ ничем не отличается от той, что используется в случае с детерминированной продолжительностью работ. Однако продолжительность найденного критического пути также будет иметь две оценки – ожидаемую и погрешность. Ожидаемая продолжительность критического пути равна сумме ожидаемых продолжительностей критических работ, а погрешность продолжительности критического пути равна сумме дисперсий критических работ.

В этом случае говорить о том, что комплекс работ будет завершен к какой-то определенной дате (т.е. будет иметь какую-то фиксированную продолжительность выполнения Tk), можно лишь с некоторой вероятностью P(Tk < x) = P(TkN < z), определяемой по таблицам стандартного нормального распределения вероятностей, причем

TkN=(x – mk )/sk ,

где: mk – ожидаемая продолжительность критического пути, а sk – квадратный корень из погрешности продолжительности критического пути.

Рассмотрим в качестве примера сетевую модель, определенную следующей табл. 4:

Таблица 4

Работа	Предшественники	Оптимистическая оценка продолжительности	Наиболее вероятная оценка продолжительности	Пессимистическая оценка продолжительности
A	-	4	6	10
B	-	3	5	8
C	-	2	4	7
D	A	6	8	12
E	C	5	10	15
F	A	9	12	16
G	F	15	18	22
H	B,D,E	7	10	16

Результаты расчета ожидаемой продолжительности выполнения работ и ее дисперсии приведены в табл. 5:

Таблица 5

Работа	Ожидаемая продолжительность	Дисперсия продолжительности
A	6,33	1,00
B	5,18	0,69
C	4,17	0,69
D	8,33	1,00
E	10,0	2,78
F	12,17	1,36
G	18,17	1,36
H	10,5	2,25

Сетевой график и его разметка с полученными временными характеристиками работ представлены на рис. 11:

Критический путь сетевого графика, приведенного на рис. 11, составляют работы A–F–G. Ожидаемая продолжительность критического пути равна 6,33 + 12,17 + 18,17 = 36,67, а суммарная погрешность продолжительности критического пути равна 1 + 1,36 + 1,36 = 3,72.

Рисунок 11. Сетевой график по данным из табл. 4 и 5

Однако полученная ожидаемая продолжительность критического пути не означает, что весь комплекс работ, описанный сетевым графиком, будет завершен именно в течение данного промежутка времени. Утверждать, что этот комплекс работ будет завершен именно в данный промежуток времени, можно только с вероятностью 0,5, так как:

P(Tk < (37,7–36,7)/1,93)= P(TkN < 0)  0,5.

Если отобразить графически кривую нормального распределения вероятностей, которому соответствует, как предполагается, распределение вероятностей продолжительности выполнения комплекса работ, то нетрудно увидеть, что кумулятивная вероятность до математического ожидания будет равна именно половине всей площади под кривой распределения (см. Рис. 12).

Рисунок 12. Кривая нормального стандартного распределения вероятностей

С таким же успехом можно определить вероятность завершения комплекса работ до любого директивного срока Х, например, до Х=38. Тогда:

P(Tk  (38-36,7)/1,93)= P(TkN < 0,69)  0,7549.

Кроме того, можно решить и обратную задачу, т.е. определить тот срок, к которому рассматриваемый комплекс работ может завершиться с некоторой заданной вероятностью Pd. Зная Pd, можно воспользоваться нормальным стандартным распределением (в форме таблиц или с помощью известной функциональной зависимости, описываемой интегралом нормального стандартного распределения ) и найти zd, а имея zd, продолжительность критического пути Тd, соответствующая заданной вероятности Pd, будет равна Тd= zdsk + mk.

Так, для рассматриваемого здесь примера промежуток времени, в течение которого комплекс работ, описываемых сетевым графиком, будет завершен с вероятностью 0,95, равен:

Pd = 0,95  zd = 1,65  Тd = zdsk + mk = 1,65  1,93 + 36,67 = 39,85.

Практически любой учебник по теории вероятностей содержит таблицы нормального стандартного распределения вероятности, которые можно использовать для решения описанной выше задачи.

Анализ соотношения между временем и затратами на выполнение проекта

Проектное управление, как уже отмечалось, базируется на теории и методах сетевого моделирования. Однако сетевые модели являются упрощенными представлениями реальных ситуаций, прежде всего, из-за того, что в них главное внимание сосредотачивается только на сроках выполнения отдельных работ и комплекса в целом, но совсем не учитывается потребность в ресурсах, их стоимость и наличие.

В реальных условиях выполнение отдельных или даже всех работ проектного комплекса можно ускорить путем выделения для них большего количества ресурсов (финансовых, трудовых, материальных). Это, конечно же, приводит к увеличению общих прямых затрат на выполнение работ. Вместе с тем, появляется множество различных комбинаций продолжительностей работ, при которых может быть получена некоторая требуемая плановая продолжительность проекта. Каждая комбинация может давать различные значения общей стоимости проекта.

Анализ соотношения между сроками и затратами имеет целью составление календарного плана, обеспечивающего минимальные затраты при данной продолжительности проекта.

Рассмотрим в качестве примера простой проект, состоящий из 8-ми работ, исходная информация по которым представлена в табл. 6.

Таблица 6

Работа		Нормальные сроки		Сжатые сроки		Суточное прираще ние затрат, доллары
Текущая	Предшеств.	Продолж., сутки	Затраты, доллары	Продолж., сутки	Затраты, доллары
A	-	4	210	3	280	70
B	-	8	400	6	560	80
C	A	6	500	4	600	50
D	A	9	540	7	600	30
E	B,C	4	500	1	1100	200
F	B,C	5	150	4	240	90
G	E	3	150	3	150	0
H	D,F	7	600	6	750	150
			3050		4280

Сетевая модель проекта показана на рис. 13.

Рисунок 13. Сетевая модель проекта по данным табл. 6

Каждая работа может выполняться за разное время – от верхнего “нормального” срока при некоторых “нормальных” затратах до меньшего “сокращенного” срока при соответствующих более высоких затратах. Если предполагается, что компромиссное соотношение между временем и затратами для каждой работы является линейным, то затраты при промежуточных продолжительностях работы, лежащих между нормальными и сокращенными сроками, легко определить с помощью единичного (суточного) приращения затрат для каждой работы. Например, затраты на выполнение работы В за 7 суток вместо 8 равны 400 долл. + (8-7) х 80 долл. = 480 долл.

Если заданы “нормальные” продолжительности всех работ, то продолжительность проекта составит 22 суток, что видно из рис. 14

.

Рисунок 14

Как показано на рис. 15, соответствующая стоимость выполнения всего проекта составит 3050 долларов. Заметим, что принятие неправильного решения, согласно которому ускоряется выполнение работ, не лежащих на критическом пути, не приводит к сокращению продолжительности проекта. Однако при этом стоимость проекта возрастает до величины 3870 долларов. Таким образом, “сжимать” сроки выполнения проекта можно по-разному, и задача состоит в том, чтобы сжимать с минимально возможным увеличением общей стоимости проекта.

В рассматриваемом примере общая стоимость проекта определяется суммой прямых затрат на выполнение каждой из работ.

Между верхним и нижним значениями стоимости проекта при продолжительности 22 суток возможны несколько других значений в зависимости от того, срок выполнения каких некритических работ сокращается.

Если устанавливаются сокращенные сроки выполнения всех работ, то продолжительность осуществления проекта можно сократить до 17 суткам, но, как видно из рис. 15, стоимость проекта при этом возрастет до суммы в 4280 долларов. Однако, продолжительность проекта, равную 17 суток, можно достигнуть при меньших затратах без ненужного ускорения отдельных работ. Так, работа B может продолжаться не 6, а 7 суток, работа D – не 7, а 8 суток, а работа E – не 1, а 4 суток. Если все остальные работы выполняются в свои “сжатые” сроки, стоимость выполнения проекта в течение 17 суток снижается до 3570 долларов.

Рисунок 15

В рассмотренном простом примере линия минимальных прямых затрат была построена методом проб и ошибок. Однако в реальных случаях, когда рассматриваются проекты с сотнями и тысячами работ, такая технология поиска решения невозможна. Поэтому применяются различные систематические вычисления, в том числе и методы математического программирования, позволяющие быстро определить кривую минимальных затрат при любом возможном значении продолжительности проекта. Некоторые из таких методов предназначены для использования в тех случаях, когда компромиссные соотношения между временем и затратами являются нелинейными; многие из них позволяют получить кривую минимальных общих затрат (равных сумме прямых и косвенных затрат).

Если прямые затраты определяются для каждой работы в отдельности и зависят, как правило, от объема и интенсивности использования привлекаемых для ее выполнения ресурсов, то косвенные затраты рассчитываются на проект в целом и поэтому их величина, как правило, исчисляется в пересчете на каждую единицу времени проекта (затрат/час, затрат/день и т.п.).

Минимизация общей стоимости при заданной продолжительности проекта

Если предполагается, что продолжительность проекта не должна (или не может) меняться по каким-либо причинам, то косвенные затраты как часть общей стоимости проекта могут не учитываться при расчетах, так как они остаются постоянной величиной. Поэтому общая стоимость проекта в данном случае будет равна сумме прямых затрат, зависящих от продолжительности каждой работы в отдельности.

Продолжительность любой работы проекта можно регулировать количеством ресурсов, выделяемых для ее выполнения. В общем случае можно предположить, что эта продолжительность может изменяться между двумя границами (пессимистической оценкой) и (оптимистической оценкой). Однако, в отличие от метода PERT, в данном случае считается, что продолжительностью работ можно управлять путем выделения на их выполнение больших или меньших ресурсов. Продолжительность работы соответствует нормальному времени работы (i,j) и ее минимальной стоимости и называется нормальной продолжительностью. Продолжительность работы соответствует такому времени выполнения работы (i,j), когда она ускорена до предела. Она называется сжатой продолжительностью. Стоимость выполнения работы в такие сроки максимальна.

Обозначая через c_ij стоимость работы (i,j), можно допустить, что C_ij = f_ij(t_ij) в общем случае представляет из себя функцию нелинейного вида, как показано на рис. 16. Стоимость возрастает, когда убывает вплоть до границы , за которой работа уже просто не может выполняться. Представляется весьма правдоподобным, что функция продолжительности работы проходит через очень пологий минимум и затем возрастает в силу ненормальных условий работы, связанных, например, с недостатком рабочей силы или материалов. Таким образом, ее форма скорее напоминает параболу.

Рисунок 16

В то же самое время практика показывает, что чаще всего c_ij на отрезке d_ij  t_ij  D_ij является линейной функцией от t_ij, для которой несложно найти коэффициент обратной пропорциональности s_ij продолжительности и стоимости работы, если известны стоимость нормальной продолжительности N_ij и стоимость “сжатой” продолжительности R_ij:

Пример расчета таких коэффициентов пропорциональности приведен в табл. 7.

Таблица 7

Работа	Предшеств.	(дни)	(дни)	($)	($)	($ в день)
A	-	9	3	900	6300	900
B	-	7	6	2800	3300	500
C	A	10	2	7000	16600	1200
D	A	12	6	8400	13800	900
E	B	12	4	7200	12800	700
F	D,E	6	6	4900	4900	0
G	D,E	6	4	3000	6200	1600
H	G	14	12	4200	5200	500
I	G, F	8	3	3200	6700	700

Построим опорный (первоначальный) план выполнения описанного в табл. 7 проекта, взяв в качестве исходных продолжительностей работ комплекса любые значения в интервале d_ij  t_ij  D_ij, построим сетевую модель, соответствующую этим исходным данным (см. Рис. 17), и рассчитаем свободные резервы времени работ (см. Табл. 8).

Рисунок 17. Сетевая модель проекта по данным табл. 7

Таблица 8

Работа	(дни)		Свободный резерв		Экономия общей стоимости
A	7	2	0	0	0
B	6	1	0	0	0
C	4	6	10	6	7200
D	8	4	0	0	0
E	8	4	1	1	700
F	6	0	0	0	0
G	5	1	0	0	0
H	12	2	0	0	0
I	5	3	6	3	2100

Для уменьшения общей стоимости проекта при сохранении продолжительности его выполнения в пределах продолжительности критического пути, необходимо уменьшить свободные резервы времени некритических работ с соблюдением условия d_ij  t_ij  D_ij. Теоретически у каждой работы есть резерв “растяжения” (D_ij - t_ij), однако не у всех работ есть свободный резерв времени, а даже у тех работ, которые имеют свободный резерв времени, он может быть значительно меньше теоретического резерва “растяжения”. Поэтому, корректирующее воздействие на “растяжение” k_ij с целью уменьшения общей стоимости проекта в пределах продолжительности установленного критического пути для работы (i,j) определяется соотношением k_ij = min {(D_ij-t_ij)FF_ij}, где FF_ij – свободный резерв работы (i,j).

В рассматриваемом примере может быть увеличена продолжительность только трех работ – C, E, I, причем продолжительность выполнения работы C может быть увеличена на 6 дней, E – на 1 день и I – на 3 дня. Суммарная экономия общей стоимости проекта будет равна 1200 х 6+700 х 1+700 х 3 = 10000. До сжатия общая стоимость проекта равнялась 62200, после “растяжения” трех указанных работ она стала 52200.

В данном примере критический путь остался без изменений. Однако, в других случаях после “растяжения” могут появиться новые критические пути и работы, на которые придется обращать основное внимание.

Не следует думать, что полученный в результате проделанной процедуры “растяжения” план проекта является оптимальным по стоимости и времени. Был получен план, минимальный по стоимости при заданной продолжительности критического пути, который в общем случае может быть очень далек от оптимального.

Если задаваемая продолжительность меньше критического пути опорного плана, то сначала последовательно “сжимаются” работы на критическом пути (по принципу “чем дешевле сжатие, тем раньше оно должно быть выполнено”), а затем проделывается описанная выше процедура.

Ускорение проекта при минимизации его общей стоимости

Более близкий к оптимальному план выполнения проекта может быть получен посредством осуществления процедуры ускорения проекта при минимизации общей стоимости. При этом общая стоимость должна включать как сумму прямых, так и сумму косвенных затрат.

Добавим к рассмотренному в предыдущем пункте примеру условие, что косвенные затраты на реализацию проекта определяются из расчета $ 1500 в день. Кроме того, выберем в качестве опорного плана проекта его так называемый “нормальный” план, когда продолжительность выполнения каждой из работ комплекса максимальна, т.е. “нормальна”. Все остальное, в том числе логика выполнения работ, коэффициенты пропорциональности стоимости и продолжительности их выполнения, остаются без изменения.

Временные параметры нового опорного плана (см. Табл. 9), естественно, будут отличаться от тех, что представлены на рис. 17.

Таблица 9

Работа	Предшественники	(дни)	Свободный резерв
A	-	9	0
B	-	7	0
C	A	10	8
D	A	12	0
E	B	12	2
F	D,E	6	0
G	D,E	6	0
H	G	14	0
I	G,F	8	6

Сетевая модель, соответствующая этим исходным данным, представлена на рис. 18.

Рисунок 18. Сетевая модель проекта по данным табл. 9

Критический путь проекта в опорном плане – [A,D,G,H], а его продолжительность равна 41 дню. Общая стоимость проекта в опорном плане равна:

• Прямые затраты: 900+2800+7000+8400+7200+4900+3000+4200+3200=41600

• Косвенные затраты: 1500 х 41 = 61500

• Всего: 103100

Алгоритм поиска плана, одновременно ускоряющего выполнение и минимизирующего общую стоимость проекта, предполагает выполнение следующих действий.

Поскольку ускорение выполнения проекта всегда связано с ускорением выполнения критических работ, постольку алгоритм предполагает уделение критическим работам основного внимания.

На каждом шаге из числа критических работ выбирается такая работа, которая может дать максимальное сокращение критического пути. Сжатие выбранной работы не должно превышать минимального свободного резерва, который рассчитан для всех работ данного варианта плана проекта (исключая 0). Если таких работ несколько, то выбирается та из них, которая имеет наименьший коэффициент обратной пропорциональности s. Если имеется несколько критических путей, то для того, чтобы получить эффект ускорения проекта в целом, сжатие критических работ должно производиться одновременно на всех этих путях. Производится “сжатие” выбранной работы (работ), строится новый план проекта, рассчитываются его временные параметры, определяются новая сумма прямых затрат (с учетом прироста стоимости выполнения сокращенной работы) и сумма косвенных затрат (с учетом новой продолжительности критического пути). Если общая стоимость проекта в новом варианте его плана оказывается меньше (либо равной), чем в предыдущем варианте, то новый вариант принимается за опорный и описанная выше процедура его ускорения повторяется. Если же общая стоимость проекта в новом варианте оказывается больше, чем в предыдущем варианте, то принимается решение об остановке алгоритма, а за оптимальный берется предыдущий вариант плана.

Применим описанный алгоритм к примеру, приведенному выше.

Таблица 10

Рисунок 19. Сетевая модель проекта после 1 шага алгоритма ускорения

Рисунок 20. Сетевая модель проекта после 2 шага алгоритма ускорения

Рисунок 21. Сетевая модель проекта после 3 шага алгоритма ускорения

Все последующие сжатия работ приводят к удорожанию проекта в целом, так как экономия на косвенных затратах не перекрывает дополнительных прямых затрат. Следовательно, после 3 шага получен оптимальный план проекта.

В табл. 11 представлены продолжительности работ и свободные резервы времени их выполнения на каждом шаге алгоритма оптимизации.

Таблица 11

	Шаг 1		Шаг 2		Шаг 3		Шаг 4
Работа	/	Свободный резерв	/	Свободный резерв	/	Свободный резерв	/	Свободный резерв
A	9 / 6	0	9 / 6	0	9 / 6	0	8 / 5	0
B	7 / 1	0	7 / 1	0	7 / 1	0	6 / 0	0
C	10 / 8	8	10 / 8	8	10 / 8	6	10 / 8	6
D	12 / 6	0	12 / 6	0	10 / 4	0	10 / 4	0
E	12 / 8	2	12 / 8	2	12 / 8	0	12 / 8	0
F	6 / 0	0	6 / 0	0	6 / 0	0	6 / 0	0
G	6 / 2	0	6 / 2	0	6 / 2	0	6 / 2	0
H	14 / 2	0	12 / 0	0	12 / 0	0	12 / 0	0
I	8 / 5	6	8 / 5	4	8 / 5	4	8 / 5	4

Сглаживание потребности в ресурсах

Несмотря на то, что потребление ресурсов само по себе находит отражение в стоимости как отдельных работ, составляющих проект, так и в стоимости проекта в целом, на практике повсеместно приходится сталкиваться с ситуацией, когда потребность в том или ином виде физического ресурса в конкретный момент времени превышает имеющиеся возможности его обеспечения. Такие ситуации возникают в силу следующих причин:

• Стремление сократить время выполнения работы приводит к неправильному решению в отношении выделяемых на нее ресурсов. Это – достаточно тривиальная ситуация, как правило, обусловленная невнимательным отношением к ограничениям по проекту. Нельзя назначить на выполнение работы, скажем, 3 исполнителя, если в наличии только 2. Такую ситуацию легко избежать при использовании компьютерных систем поддержки проектного управления, таких как Microsoft Project, в которых запрограммирована процедура проверки на непротиворечивость условий проекта.

• Другое дело, когда для каждой в отдельности взятой работы проекта условия соответствия ограничениям по ресурсам соблюдены, но топология сетевой модели проекта оказывается причиной запараллеливания нескольких работ, предусматривающих использование одинаковых ресурсов, что приводит к соответствующему увеличению суммарной потребности в них в определенные моменты времени. Возникает конфликтная ситуация, суть которой, коротко, заключается в том, что в рассматриваемый момент времени потребность в ресурсах превышает возможности, а значит для какой-то (или каких-то) из работ оказывается невозможным осуществить выполнение так, как это предполагается текущим планом. Данная ситуация, как правило, становится предметом тщательного анализа, поскольку требует своего разрешения на стадии планирования проекта. Конфликт должен и может быть разрешен с помощью перепланирования проекта, а целью этого перепланирования должно быть либо максимальное сокращение перерасхода ресурсов без увеличения общего времени выполнения проекта, либо приведение потребности в ресурсах в соответствие с установленными ограничениями (пусть даже за счет некоторого удлинения сроков выполнения проекта), либо комбинация этих двух целей. В любом случае речь идет о сглаживании потребности в ресурсах, только в первом случае, как бы предполагается, что имеются четкие ограничения “по горизонтали”, т.е. по срокам осуществления проекта, во втором случае – что имеются четкие ограничения “по вертикали”, т.е. по суммарной потребности в ресурсах, а в третьем случае – что имеются четкие установки относительно общей стоимости проекта, а именно, что она должна быть минимальна.

Общие принципы сглаживания потребности в ресурсах очень просты.

Первый принцип исходит из того, что, как правило, многие из параллельно запланированных работ, требующих одних и тех же ресурсов, имеют резервы времени их выполнения, предполагающие, что их осуществление может быть отложено на некоторое время безо всякого влияния на общую продолжительность выполнения всего проекта в целом. Поэтому, распараллеливание работ приводит к сглаживанию потребности в ресурсах (принцип распараллеливания).

Второй принцип исходит из того, что продолжительность выполнения некоторых работ зависит от объема выделяемых для них ресурсов. Поэтому, если у таких работ имеются также и резервы времени, то можно безболезненно для проекта в целом пойти на снижение интенсивности выполнения этих работ, что приведет к сглаживанию потребности (принцип снижения интенсивности работ).

Применение этих двух принципов (в той мере, в какой это возможно) необязательно обеспечит приведение суммарной потребности в ресурсах в соответствие с установленными ограничениями. Иными словами, чтобы удовлетворить эти установленные ограничения, может потребоваться увеличение общих сроков выполнения проекта. Это увеличение может быть оправдано в том случае, когда стоимость “удлинения” продолжительности проекта окажется меньше стоимости “превышения лимита” ресурса.

Однако, несмотря на простоту и понятность общих принципов, на которых строится сглаживание потребности проекта в ресурсах, расчетные алгоритмы оказываются очень и очень трудоемкими. Следует признать, что пока не разработано метода прямого поиска оптимального решения этой задачи и на практике процедуры сглаживания связаны либо с полным перебором возможных вариантов топологии проектного плана (в этом случае оказывается возможным доказать оптимальность варианта плана), либо с применением некоторых эвристических правил выстраивания квазиоптимальной топологии (например, “наиболее короткая работа должна выполняться первой”). И в том, и в другом случае нельзя обойтись без специального программного обеспечения, не только из-за трудоемкости решения задачи, но из-за того, что при ее решении слишком высока вероятность допустить расчетную ошибку.

Следующий небольшой пример (см. Рис. 22) позволит лучше представить, за счет чего происходит сглаживание потребности в ресурсах и как отличить лучший (с точки зрения равномерности потребности в ресурсах) вариант проектного плана от остальных. Сетевая модель проекта, который будет анализироваться на предмет сглаживания потребности в ресурсах, представлена на рис. 8.

Рисунок 22.

К анализу потребности в ресурсах приступают с построения графика Ганта проекта, на котором работы откладываются на временной шкале от ранних сроков начала их выполнения. Параллельно с графиком Ганта строится гистограмма изменения потребности во времени, ось абсцисс которой – это временная шкала выполнения проекта, а ось ординат – суммарная (по всем выполняемым в данный момент времени работам) потребность в ресурсах. Исходный график Ганта и гистограмма потребности в ресурсах представлены на рис. 23.

Среднедневная вариация потребности в ресурсах = 2,66

Рисунок 23.

Расчеты показывают, что средняя дневная потребность в ресурсе составляет приблизительно 7. Однако в некоторые дни она может быть равна 12, а в другие 3.

Среднедневная вариация потребности в ресурсах = 1,71

Рисунок 24.

Вместе с тем, у работ A, G, I и L имеется свободный резерв времени (который изображен на графике Ганта серой волнистой линией), в пределах которого их выполнение может откладываться. Если отложить, например, начало выполнения работы А на 6 дней (см. Рис. 24), то можно существенно сгладить потребность данного проекта в ресурсе. Если исходный план выполнения проекта предполагал в отдельные дни потребность, равную 12, и среднедневная вариация потребности (отклонение от средней) составляла плюс-минус 2,66, то после изменения сроков выполнения работы А максимальная потребность будет снижена до 11, а среднедневная вариация потребности составит плюс-минус 1,71.

Дальнейший анализ вариантов может привести к такому решению, когда начало выполнения работы А откладывается на 11 дней, а работы G – на 2 дня. Это позволяет свести максимальную потребность в ресурсе к 9, а среднедневную вариацию потребности к 1,69 (см. Рис. 25).

Среднедневная вариация потребности в ресурсах = 1,69

Рисунок 25.

Поиск оптимальных календарных планов проектов при заданных ограничениях по ресурсам представляет скорее теоретический интерес, чем практическое значение.

Нецелесообразность применения методов линейного программирования для данного класса задач была обнаружена достаточно рано (уже в 60-е годы). Для сетевой модели с 55 работами и четырьмя видами ресурсов требуется решение системы более 5000 уравнений с 1600 переменными.

Приведение проекта в соответствие с ограничениями по ресурсам

На практике из-за того, что при построении сетевых моделей проектов изначально невозможно учесть все ограничения по ресурсам, времени и стоимости, очень часто приходится сталкиваться с ситуацией, что полученный в конце концов календарный план проекта нельзя считать удовлетворительным именно из-за того, чтов отдельные периоды времени требуется привлечение гораздо больших ресурсов, чем на самом деле может быть выделено. Тогда возникает необходимость в решении задачи изменения опорного календарного плана проекта с целью приведения проекта в соответствие с ограничениями по ресурсам.

Наибольшее распространение для решения такой задачи получили разнообразные эвристические методы из-за своей относительной простоты и вместе с тем неплохого качества получаемых решений (зачастую мало отличающихся от тех, которые можно было бы получить, применяя сложные методы оптимизации). Все эти методы основаны на принципе использования эвристик (определенных правил) перемещения ресурсов между работами и изменения календарных сроков выполнения работ. Один из алгоритмов, основанных на подобных эвристиках, приводится ниже.

Алгоритм приведения проекта в соответствие с ограничениями по одному ресурсу:

Шаг 1. Определяем список работ, которые могут начинаться в день Di (i=1, 2, 3, ..., N). Сначала рассматривается первый день. Переход к Шагу 2.

Шаг 2. Работы упорядочиваются в порядке возрастания их свободных резервов времени. Переход к Шагу 3.

Шаг 3. Из упорядоченного списка выбирается работа Х и определяется, достаточно ли имеется ресурсов для начала ее выполнения в день Di? Если ДА, то переходим к Шагу 4. Если НЕТ, то переходим к Шагу 9.

Шаг 4. Начало выполнения работы Х окончательно назначается на день Di , а наличное количество ресурсов уменьшается на сумму ресурсов, требуемых для выполнения работы Х. Переход к Шагу 5.

Шаг 5. Проверяется условие, все ли работы из списка тех, что могут начинаться в день Di, рассмотрены? Если НЕТ, то переход к Шагу 6. Если ДА, то переход к Шагу 7.

Шаг 6. Рассмотренная и закрепленная только что за днем Di работа Х исключается из списка и переходим к Шагу 3.

Шаг 7. Проверяется условие, имеются ли еще работы в проекте, для которых не произведено окончательное закрепление сроков начала выполнения? Если ДА, то переход к Шагу 8. Если НЕТ, то переход к Шагу 13.

Шаг 8. Выбирается следующий день (Di = Di + 1) и переходим к Шагу 1.

Шаг 9. Проверяется условие является ли работа Х критической? Если ДА, то переход к Шагу 11. Если НЕТ, то переход к Шагу 10.

Шаг 10. Возможный срок начала работы откладывается на 1 день. Переход к Шагу 5.

Шаг 11. Проверяется условие, можно ли передать данной работе ресурсы с некритических работ, выполнение которых уже распланировано на этот день? Если НЕТ, то переход к Шагу 10. Если ДА, то переход к Шагу 12.

Шаг 12. Начало выполнения критической работы Х окончательно назначается на день Di, приводится в соответствие количество ресурсов на связанных работах, а наличное количество ресурсов уменьшается на сумму ресурсов, требуемых для выполнения работы Х (за минусом того количество ресурсов, которое было перенесено с другой работы). Переход к Шагу 5.

Шаг 13. Алгоритм считается завершенным.

Оценка инвестиционной привлекательности проектов

Принимая решение о начале того или иного проекта, необходимо, хотя бы в общих чертах, оценить будущую выгоду от его реализации, риск потери инвестиций и неопределенность будущих условий.

Следует иметь в виду, что инвестиционная привлекательность проекта тем выше, чем короче период его окупаемости, при прочих равных условиях (прежде всего при условии невысокого риска).

Например, имеется два проекта, А и В. Стоимость проекта А $ 20000, а проекта В – $ 16000. Через 4 года и тот и другой проект принесут прибыль, равную $ 7000. Казалось бы проект В выгоднее (меньше затрат, а прибыль та же). Однако, рассмотрим движение денежной наличности (см. Табл.12):

Таблица 12

	0	1	2	3	4
А	-20000	10000	7500	5000	4500
В	-16000	11000	2000	3000	7000

Анализ движения денежной наличности свидетельствует, что срок окупаемости проекта А – 2,5 года, а проекта В – 3 года. С этой точки зрения проект В менее выгоден.

Принимая решение относительно инвестиций в какой-либо проект, необходимо также иметь в виду, что со временем стоимость денег меняется и это изменение зависит от процентных ставок, которые действуют в данной стране. Иными словами, вместо того, чтобы вкладывать деньги в рискованный проект в надежде получить прибыль, вы можете положить деньги в банк и получить некоторый процент на них.

Если процентная ставка равна r, то сумма денег Р, положенная вами в банк на n лет, по истечении этого срока возрастет до величины:

An=P (1+r)n.

Это означает, что доход An , который предполагается получить от инвестиций через n лет, в настоящий момент необходимо рассматривать с учетом коэффициента дисконтирования, равного 1/(1+r)n . Это дает нам так называемую приведенную к настоящему моменту стоимость будущих денег (PV).

Для нашего примера, если процентная ставка устанавливается на уровне 15%, то коэффициенты дисконтирования и приведенная стоимость проектов по годам будет следующей (см. Табл. 13):

Таблица 13

	0	1	2	3	4
15%	1	0.8696	0.7561	0.6575	0.5718
А	-20000	10000	7500	5000	4500
PV(A)	-20000	8696	5671	3288	2573
NPV(A)				-2344	+228
В	-16000	11000	2000	3000	7000
PV(B)	-16000	9566	1512	1973	4003
NPV(B)				-2949	+1054

Сумма приведенной стоимости за n лет (включая первоначальные инвестиции со знаком минус) дает так называемую чистую приведенную стоимость проекта (NPV).

• Если NPV > 0, то проект прибыльный;

• Если NPV = 0, то проект самоокупаемый;

• Если NPV < 0, то проект неприбыльный.

В нашем примере видно, что по истечении 3 лет ни один из проектов еще не дает прибыль, зато через четыре года прибыль проекта В оказывается выше, чем у проекта А.