
- •Екзаменаційний білет № 1
- •Прикладна гравіметрія як метод геофізики. Зв’язок з іншими дисциплінами.
- •Пряма і обернена задачі гравіметрії. Їх головні риси.
- •3. Динамічні методи вимірювання прискорення сили тяжіння.
- •Екзаменаційний білет № 2
- •1. Одиниці вимірювання сили тяжіння і других похідних гравітаційного потенціалу (в системах si та сгс).
- •2. Зв’язок гравітаційного і магнітного потенціалів. Теорема Пуассона.
- •3. Статичні методи вимірювання прискорення сили тяжіння.
- •Екзаменаційний білет № 3
- •Сила тяжіння і відцентрова сила. Їх розподіл на поверхні Землі.
- •2. Класифікація гравіметричних зйомок, їх задачі.
- •3. Астазування. Переваги астазованих систем.
- •1. Другі похідні гравітаційного потенціалу, їх фізичний зміст.
- •Екзаменаційний білет № 5
- •1. Кривизни. Їх значення при гравіметричних дослідженнях.
- •2. Градієнти гравітаційного поля Землі.
- •3.Сучасна технологія інтерпретації гравітаційних аномалій. Екзаменаційний білет № 6
- •1. Густина гірських порід. Фактори, що її визначають
- •2. Найважливіші ознаки кондиційності гравіметра
- •3.Особливості якісної інтерпретації гравіметричних досліджень для ізометричних та видовжених аномалій.
- •1. Густина осадочних гірських порід. Основні фактори, що її визначають.
- •2. Кількісна інтерпретація локальних гравітаційних аномалій для тіл правильної геометричної форми.
- •2. Застосування гравіметрії при пошуках родовищ рудних корисних копалин.
- •Екзаменаційний білет № 9
- •2. Системи комплексної інтерпретації геолого-геофізичних даних, їх особливості, задачі, які вони вирішують.
- •Екзаменаційний білет № 10
- •1. Нормальні і аномальні значення сили тяжіння. Редукція Буге. Аномалія Буге.
- •2. Обґрунтувати ефективність вивчення градієнтів та кривизн.
- •3. Особливості застосування гравіметричних методів при тектонічному районуванні.
- •Екзаменаційний білет № 12
- •Методи визначення щільності гірських порід.
- •3. Аналітичне продовження гравітаційного поля у верхній напівпростір. Його особливості.
- •Екзаменаційний білет № 14
- •1. Основні властивості потенціалу притягування
- •2. Переваги гравітаційного варіометра в порівнянні з маятниковими гравіметрами.
- •Екзаменаційний білет № 15
- •1. Опорна і рядова мережі. Їх особливості.
- •3. Пряма задача гравіметрії для горизонтального циліндра.
Екзаменаційний білет № 15
1. Опорна і рядова мережі. Їх особливості.
Зйомки проводяться рейсами, що починаються і закінчуються на опорних пунктах. Частина рейсу між двома опорними пунктами називається ланкою. Опорна мережа розбивається для обліку сповзання нуль-пункту і знаходження абсолютних значень прискорення сили тяжіння. Вона включає до 5 - 10% від загального числа точок спостереження, рівномірно розподілених по площі. Точність визначення прискорення сили тяжіння на опорних точках повинна в 1,5 - 2 рази перевищувати точність рядових спостережень. Це досягається використанням більш високоточних приладів, багаторазовими вимірюваннями на опорних точках, скорочення проміжку часу між вимірюваннями на сусідніх точках шляхом використання транспорту. При створенні опорної мережі від 50 до 100% всіх спостережень повинні складати повторні (контрольні). Існує кілька способів розбиття опорної мережі. Широко поширені вимірювання по центральній системі, коли один з опорних пунктів (центральний) має зв'язки з усіма іншими, тобто з'єднаний з кожним з них однією ланкою. Іноді розбивка мережі здійснюється за системами, які не передбачають наявності центральної точки. існує державна мережа, що включає в себе пункти 1, 2 і 3 класів точності, на яких прискорення сили тяжіння виміряна з високою точністю. Відстані між цими пунктами становлять близько 10 км, що не дозволяє використовувати їх для виявлення аномальних значень поля сили тяжіння. Проте, до них здійснюється прив'язка опорних мереж. Необхідно визначати точність опорної мережі, що характеризується середньою квадратичною помилкою. Вона виходить за контрольними спостереженнями і розраховується за формулою:
εоп = ±(Σδ2/(m-n))1/2
де δ - похибки прискорення сили тяжіння по контрольним спостереженнями (різниця між основним і контрольним виміром), m - загальне число всіх спостережень, включаючи контрольні, n - число контрольних точок. Під час зйомок на рядовий мережі передує дослідження гравіметрів, що включає в себе визначення сповзання нуль-пункту. За цими даними виділяють проміжок часу, протягом якого сповзання нуль-пункту можна вважати лінійно залежних від часу. При рядовий зйомці після закінчення цього проміжку (1 - 2 години) необхідно брати завмер на одному з опорних пунктів. Зйомка на рядових пунктах ведеться як шляхом одноразових спостережень, так і з повтореннями при зворотному ході, що дозволяє більш гнучко враховувати сповзання нуль-пункту. Для контролю точності рядовий зйомки використовуються повторні спостереження на контрольних точках, які становлять не менше 5 - 10% від загального числа точок. За ним розраховується середньоквадратична помилка рядовий мережі за формулою: εряд = ±(Σδ2/(2n-1))1/2 де n - число контрольних точок.
3. Пряма задача гравіметрії для горизонтального циліндра.
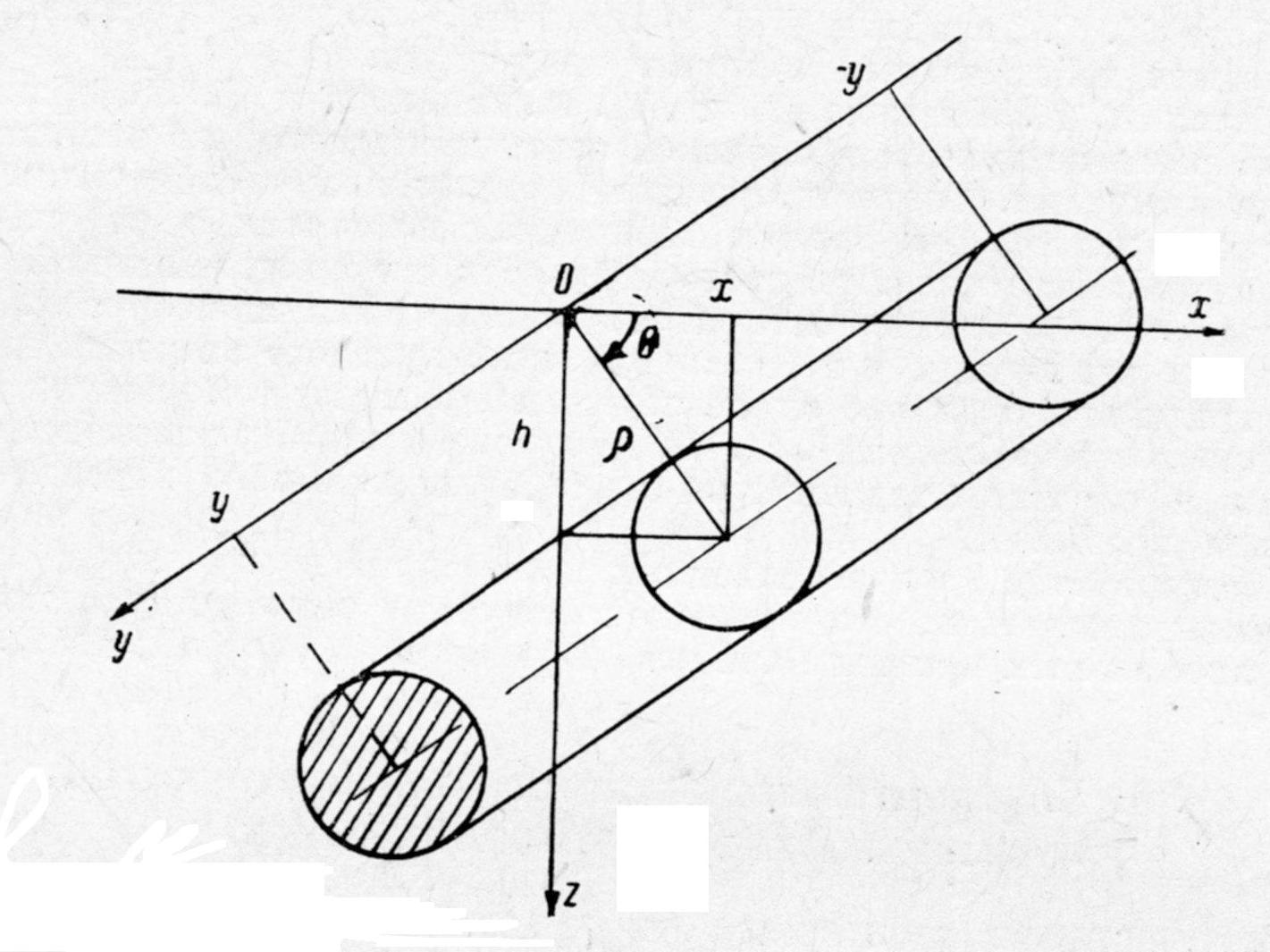
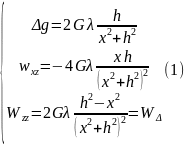
В
даному випадку λ- лінійна густина або
добуток об’ємної надлишкової густини
σ циліндру на площу його поперечного
перерізу λ=σS=σπ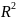 .(2)
.(2)
Розглянемо
окремо кожну з функцій, що досліджуються.
В першу чергу розглянемо величину
потенціалу сили тяжіння
 .
.
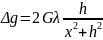 .
При λ>0 слідує,
що
скрізь додатна функція, що має максимум
при х=0, тобто на віссю циліндру; при
цьому
– функція парна, а саме
.
При λ>0 слідує,
що
скрізь додатна функція, що має максимум
при х=0, тобто на віссю циліндру; при
цьому
– функція парна, а саме
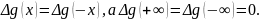
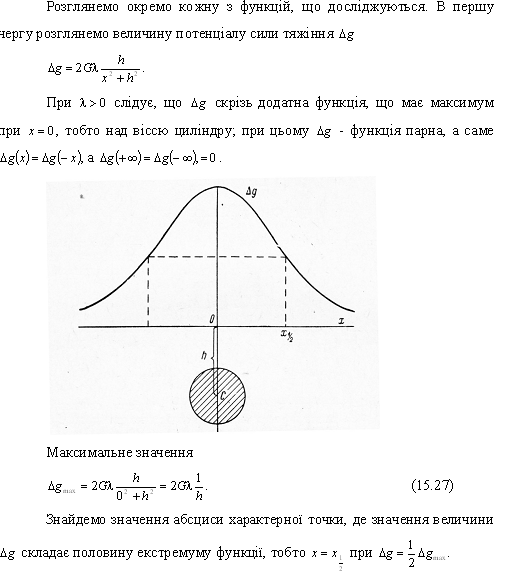
Максимальне
значення
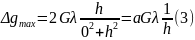 .
Знайдемо
значення абсциси характерної точки, де
складає половину екстремуму функції,
тобто х=
.
Знайдемо
значення абсциси характерної точки, де
складає половину екстремуму функції,
тобто х=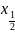 при
при
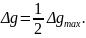 Підставляючи
це значення в ф-лу (1) , знаходимо:
Підставляючи
це значення в ф-лу (1) , знаходимо:
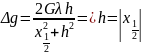 (4)
(4)
Формули
(3) і (4) дозволяють визначити значення λ
і h.
Якщо відома об’ємна густина σ, то з
формули (2) λ=σS=σπ
, можна визначити радіус циліндру R
і
глибину залягання його верхньої кромки
Н=h-R.
Представимо формулу для
в більш загальному вигляді
 (5) і розглянемо як змінюється
за вертикальним напрямком, тобто при
зміні координат z.
(5) і розглянемо як змінюється
за вертикальним напрямком, тобто при
зміні координат z.
Припустимо,
що х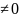 ,
тобто ми знаходимося на боковому
вертикальному профілі. Тоді
,
тобто ми знаходимося на боковому
вертикальному профілі. Тоді
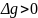 при z
< h
i
при z
< h
i
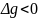 при
z
> h.
Причому
при
z
> h.
Причому
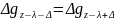
При
z=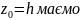 h=
h=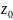 (6)
(6)
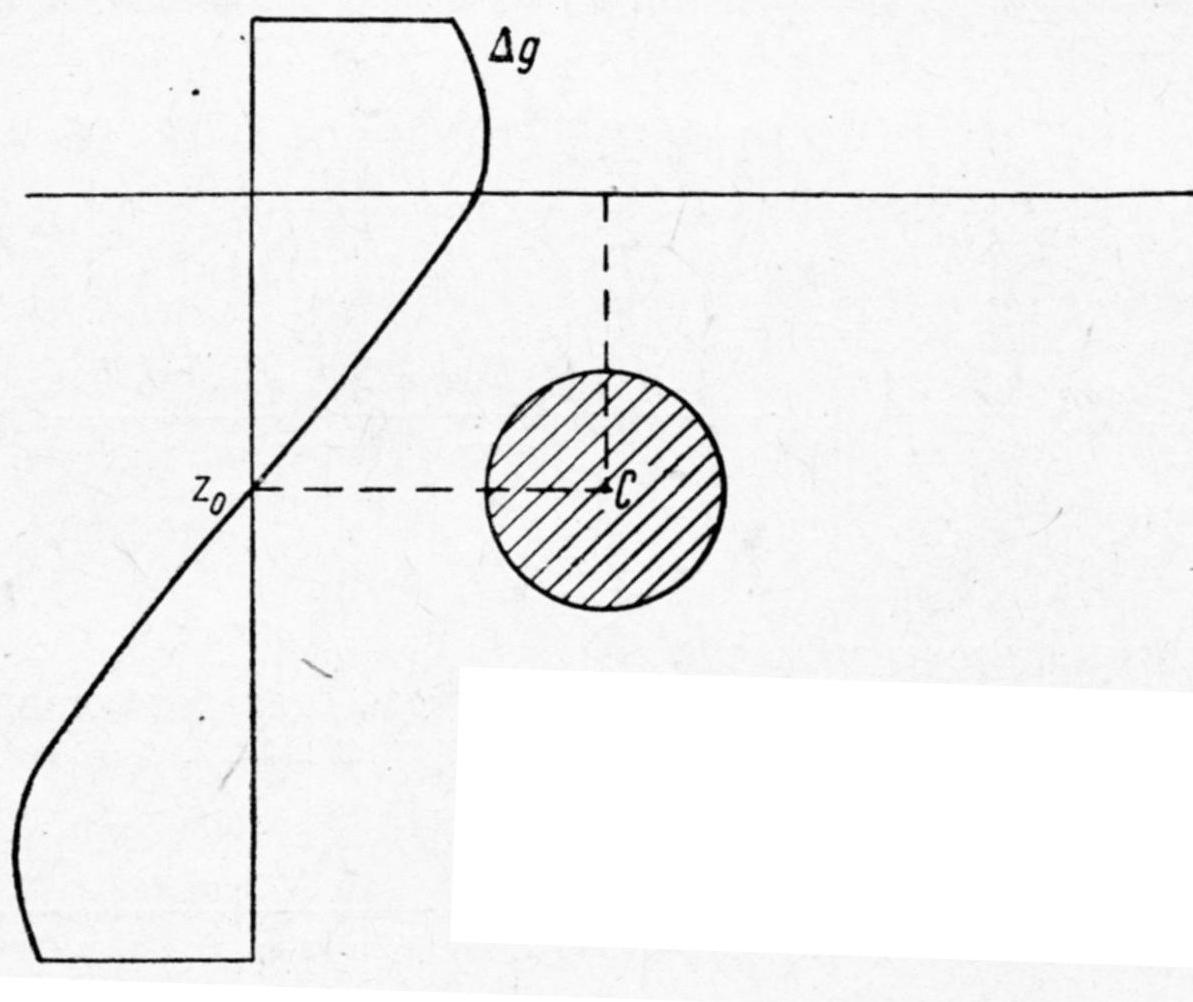
Диференціювання
по z
у формулі (5) з подальшим її похідної
нулеві . отримаємо:
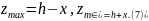 З останніх рівнянь слідує, що
З останніх рівнянь слідує, що
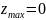 при цьому значенні х
максимальне значення
знаходиться на рівні площини спостережень.
Це дає простий спосіб визначення h,
якщо
розподіл
відомий для декількох бокових вертикальних
профілів, включаючи той, для якого x=h.
Максимальне
значення
на боковому вертикальному профілі тоді
має виглядати таким чином
при цьому значенні х
максимальне значення
знаходиться на рівні площини спостережень.
Це дає простий спосіб визначення h,
якщо
розподіл
відомий для декількох бокових вертикальних
профілів, включаючи той, для якого x=h.
Максимальне
значення
на боковому вертикальному профілі тоді
має виглядати таким чином
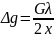 (8). Умови
(6) і (8) дозволяють визначити значення h
і
λ.
(8). Умови
(6) і (8) дозволяють визначити значення h
і
λ.
При
х=0
маємо
= .
(9),
звідки
=∞
при
.
(9),
звідки
=∞
при
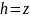 .
Тоді відповідно точка (0,h),
а саме центр стержня або циліндру
представляє собою особливу ( характерну)
точку аномалії
.
.
Тоді відповідно точка (0,h),
а саме центр стержня або циліндру
представляє собою особливу ( характерну)
точку аномалії
.
Розглянемо горизонтальний градієнт Wxz (друга похідна з формули (1). Він представляє собою функцію, яка додатна при x<0 і від’ємна при х <0, причому Wxz (-х)= Wxz(х), тобто Wxz – це непарна функція х. При х=0 і при х=+∞ Wxz перетворюється в нуль.
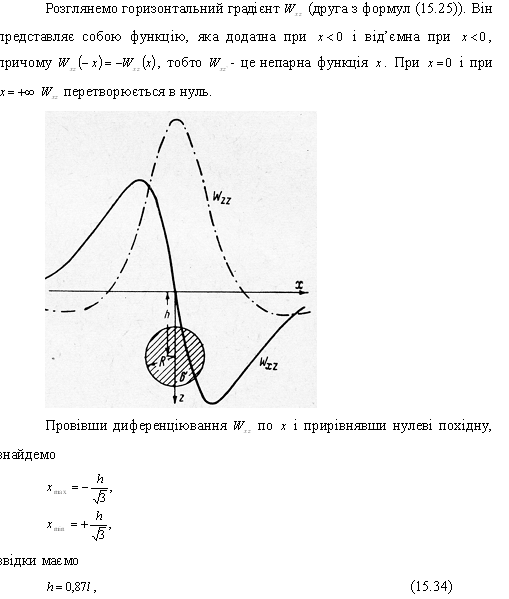
Провівши
диференціювання Wxz
по х і
прирівнявши нулеві поідну, знайдемо
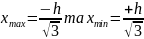 (10)
звідки
маємо h=0,871,
де I=
(10)
звідки
маємо h=0,871,
де I=
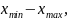 тобто відстань між точками максимуму
і мінімуму кривої Wxz.
тобто відстань між точками максимуму
і мінімуму кривої Wxz.
Значення
максимуму Wxz=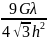 ,
звідки
λ=0,011
,
звідки
λ=0,011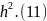
Вертикальний
градієнт Wxz
і
кривизна
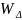 тотожно рівні між собою для стержня,
циліндру і будь-якого тіла, що нескінченно
за простяганням по осі у.
тому ц подальшому для таких тіл
нескінченного простягання введемо
єдине позначення Wxz
, маючи на увазі, що скрізь Wxz
=
.
тотожно рівні між собою для стержня,
циліндру і будь-якого тіла, що нескінченно
за простяганням по осі у.
тому ц подальшому для таких тіл
нескінченного простягання введемо
єдине позначення Wxz
, маючи на увазі, що скрізь Wxz
=
.
Якщо
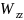 =2Gλ
=2Gλ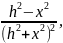 то
є функцією додатною в інтервалі
то
є функцією додатною в інтервалі
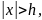 дорівнює нулеві при
дорівнює нулеві при
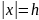 , а також при x=+∞.
Звідки
отримаємо h=
, а також при x=+∞.
Звідки
отримаємо h=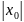 (12),
де
(12),
де
 - абсциса нульового значення Wzz.
Дослідження
похідної
- абсциса нульового значення Wzz.
Дослідження
похідної
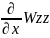 показує, що Wzz
має максимум при
показує, що Wzz
має максимум при
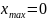 і два мінімуму при
і два мінімуму при
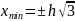 .
З
останньої умови маємо h=0,58
.
З
останньої умови маємо h=0,58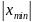 (13).
Це
є друге рівняння. Що визначає h.
Підставляючи
значення
(13).
Це
є друге рівняння. Що визначає h.
Підставляючи
значення
 в
загальну формулу Wzz
отримуємо
в
загальну формулу Wzz
отримуємо
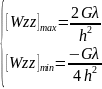 (14)
(14)
Кожне з цих співвідношень дає можливість визначити параметр λ.
