1.2.2. Понятие кода и кодирования. Моделирование дискретных источников сообщений без памяти
Символы, выдаваемые источником сообщений, обычно подаются на вход кодера, который осуществляет процесс кодирования информации.
Под кодированием информации понимают процесс преобразования информации из формы, удобной для непосредственного ее использования, в форму, удобную для передачи, хранения или автоматической обработки. Обратный процесс называется декодированием.
Кодер имеет собственный алфавит символов C = {c1, c2, ..., cK}, называемый вторичным алфавитом (за первичный алфавит принимается алфавит источника сообщений). Кроме того, кодер имеет определенный алгоритм кодирования (код).
Код – правило сопоставления каждому конкретному сообщению (символу первичного алфавита) строго определённой комбинации символов вторичного алфавита. Отдельная комбинация таких символов называется кодовым словом.
Число символов L в кодовом слове называется длиной кодового слова.
Объем алфавита K кодера, то есть число различных символов кода называют основанием кода. Например, если K = 2, 3, 4, … , то код называют бинарным (двоичным), триарным (троичным), тетрарным и т. д.
Коды, все слова которых имеют одинаковую длину, называются равномерными (блочными). Соответственно коды, в которых данное условие не выполняется, называют неравномерными.
Неравномерные коды требуют либо специальных разделительных знаков, учитывающих конец одного кодового слова и начало другого, либо должны строиться так, чтобы никакое кодовое слово не являлась передней частью (префиксом) другого кодового слова (свойство префикса). Неравномерные коды, обладающие свойством префикса, называют префиксными кодами.
Для закодированного сообщения может быть определена такая характеристика, как объем информации, под которым понимают общее число символов вторичного алфавита в сообщении.
❒ Пример 1.5. Разработка компьютерной модели дискретного источника сообщений без памяти.
Требуется разработать компьютерную модель дискретного источника сообщений без памяти, описанного в примере 1.2.
Также создадим модель кодера источника сообщений, алфавит которого будет состоять из символов «0» и «1». Примем, что кодирование производится равномерным кодом по следующему правилу:
s1 → 00; s2 → 01; s3 → 10; s4 → 11.
В качестве вводимых данных должна использоваться длина сообщения от источника.
Результатами работы модели выступают исходное сообщение, сгенерированное источником, и закодированное сообщение, выдаваемое кодером. Кроме того, требуется выводить частоты появления символов в сообщении для проверки правильности работы модели.
Для программной реализации воспользуемся интегрированной средой разработки MS Visual Studio и языком программирования Visual C#. В качестве шаблона проекта используем консольное приложение.
Программный код консольного приложения организуем в виде двух классов DiscrIS и KoderIS.
Класс DiscrIS описывает дискретный источник сообщений (рис. 1.2). В данном классе присутствует метод случайного генерирования отдельных символов в соответствии с их вероятностями (метод GenSimv).
Рис. 1.2. Исходный код класса DiskrIS (дискретный источник сообщений)
Класс KoderIS описывает дискретный источник сообщений (рис. 1.3). В данном классе помимо метода кодирования (метод KodSimv) присутствует метод, связанный с выдачей информации о частотах появления отдельных символов (метод Statist). Такая статистическая информация позволяет проверить правильность компьютерной модели источника.
Рис. 1.3. Исходный код класса KoderIS (кодер источника сообщений)
В процедуре Main() консольного приложения (рис. 1.4) создаются экземпляры классов DiskrIS и KoderIS (объекты dis и kis) и осуществляется вызов их методов. В цикле for данной процедуры через переменную строку-буфер buf осуществляется передача отдельных символов от источника к кодеру, а также происходит формирование исходного (s) и закодированного (c) сообщений.
Рис. 1.4. Исходный код метода Main() консольного приложения
Результат работы консольного приложения при длине сообщения n = 220 символов показан на рис. 1.5.
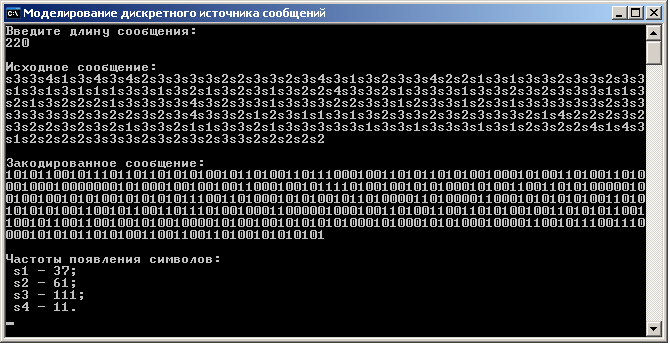
Рис. 1.5. Результат работы консольного приложения
Из полученного результата видно, что частоты появления символов в сообщении приблизительно соответствуют вероятностям этих символов. ❒