6. Сжатие информации методами Лемпела-Зива
6.1. Цель работы
Цель работы – приобрести умение производить сжатие информации с помощью методов Лемпела-Зива.
Работа рассчитана на 2 часа.
6.2. Основные теоретические сведения
Сжатием информации называется операция, в результате которой данному коду или сообщению ставится более короткий код или сообщение.
Целью сжатия информации является ускорение и удешевление процессов обработки, хранения и передачи информации.
В настоящее время разработано большое число методов сжатия информации (текстовой, графической, видео), которые могут быть классифицированы по различным признакам (рис. 6.1).
По обратимости операции сжатия информации различают две группы методов:
• Методы сжатия без потерь (методы энтропийного сжатия), позволяют полностью восстановить информацию по сжатым данным. Сжатие без потерь оставляет неизменной энтропию.
• Методы сжатия с потерями предполагают неточное восстановление сжатых данных. Сжатие с потерями основано на особенностях человеческого восприятия аудио- и видеоинформации.
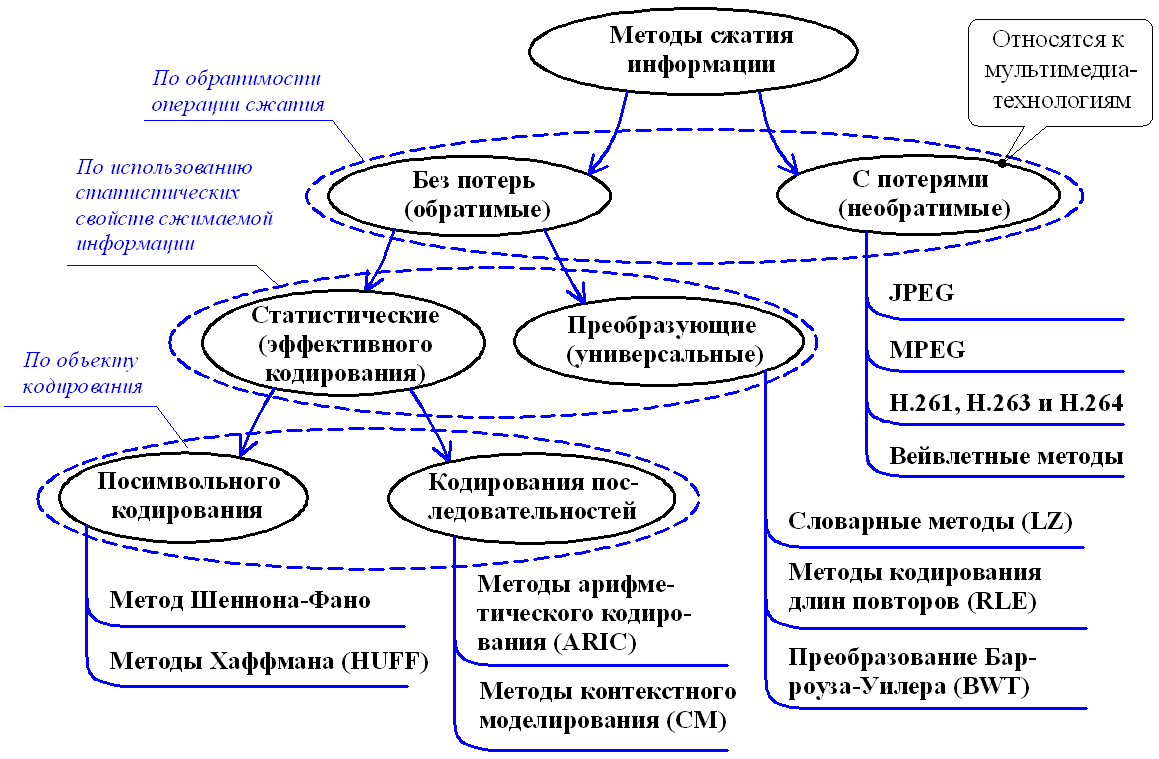
Рис. 6.1. Классификация методов сжатия информации
Основная идея алгоритмов Лемпела-Зива состоит в замене появления фрагмента в данных (группы байт) ссылкой на предыдущее появление этого фрагмента.
6.3. Порядок выполнения работы
6.4. Контрольные вопросы
1. ?
2. ?
3. ?
4. ?
5. ?
7. Построение и декодирование кода Хэмминга
7.1. Цель работы
Цель работы – приобрести умение строить и декодировать код Хэмминга для исправления одиночных ошибок в кодовых словах и обнаружения двойных ошибок.
Работа рассчитана на 4 часа.
7.2. Основные теоретические сведения
7.2.1. Блоковые корректирующие коды и их характеристики. Код Хэмминга
Блоковые корректирующие коды и их характеристики.
Блоковыми называют помехоустойчивые коды, в которых процедура кодирования заключается в разбиении входной последовательности информационных символов на блоки, содержащие m символов. Каждому информационному блоку длиной m сопоставляется k проверочных символов. Полученное кодовое слово из n = m + k символов называют кодовым блоком.
Число
несовпадающих позиций в двух кодовых
словах
и
называется
расстоянием
Хэмминга
между этими словами.
Для двоичных кодовых слов расстояние Хэмминга может быть получено как число единиц в сумме в кодовых словах по модулю 2. Правила сложения по модулю 2 определяются следующим образом:
;
;
;
.
Важной характеристикой корректирующего блокового кода C является кодовое расстояние, которое принимается равным наименьшему расстоянию Хэмминга между словами данного кода:
. (7.1)
Для блоковых кодов справедливы следующие утверждения:
1). Для того чтобы блоковый код C позволял обнаруживать все комбинации из t или менее ошибок, необходимо и достаточно, чтобы его кодовое расстояние было равно d(С) = t + 1.
2). Для того чтобы блоковый код C позволял исправлять все комбинации из t или менее ошибок необходимо и достаточно, чтобы его кодовое расстояние было равно d(С) = 2t + 1.
Для практических расчетов при определении числа проверочных символов k в коде с кодовым расстоянием d(С) = 3 используют следующие формулы:
если известна длина полного кодового слова n, то
; (7.2)
если при расчетах удобнее исходить из заданного числа информационных символов m, то
; (7.3)
где
– округление числа, стоящего в скобках,
до целого в большую сторону.
Для блоковых кодов с d(С) = 4
; (7.4)
или
. (7.5)