Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Кузбасский государственный технический университет
им. Т.Ф. Горбачева»
Д.Е. Турчин
ТЕОРИЯ ИНФОРМАЦИИ
Лабораторный практикум
Рекомендовано учебно-методической комиссией направления
подготовки бакалавра 230400 «Информационные системы и
технологии» в качестве электронного издания для использования
в учебном процессе
Кемерово 2013
Рецензенты:
Ванеев О.Н. доцент каф. ИиАПС
Турчин Денис Евгеньевич. Теория информации. Лабораторный практикум: методические указания к лабораторным работам [Электронный ресурс] для студентов очной формы обучения направления подготовки бакалавра 230400 «Информационные системы и технологии» / Д. Е. Турчин Электрон.дан. – Кемерово: КузГТУ, 2012. – 1 электрон.опт. диск (CD-ROM); зв.; цв.; 12 см. – Систем. требования: Pentium IV; ОЗУ 256 Мб; WindowsXP; (CD-ROM-дисковод); мышь. – Загл. с экрана.
В данных методических указаниях изложены содержание лабораторных работ, порядок их выполнения, а также контрольные вопросы к ним.
КузГТУ
Турчин Д.Е.
СОДЕРЖАНИЕ
Кемерово 2013 0
СОДЕРЖАНИЕ 1
H(A) = – (0,2∙log20,2 + 0,3∙log20,3 + 0,45∙log20,45 + 9
+ 0,05∙log20,05) = 0,464 + 0,521 + 0,518 + 0,216 = 9
= 1,719 (бит/символ). 9
H2(S) = – [0,242∙(0,11∙log20,11 + 0,36∙log20,36 + 28
H(A,B) = H(A) + H(B|A) = H(B) + H(A|B); (2.11) 30
H(U|S) = – [0,24∙log20,24 + 0,06∙log20,06 + 31
+ 0,38∙log20,38 + 0,32∙log20,32) + 0,271·(0,09∙log20,09 + 31
+ 0,25∙log20,25 + 0,15∙log20,15 + 0,24∙log20,24 + 31
+ 0,27∙log20,27) + 0,25·(0,18∙log20,18 + 0,33∙log20,33 + 31
+ 0,19∙log20,19 + 0,3∙log20,3) + 0,237·(0,1∙log20,1 + 31
+ 0,25∙log20,25 + 0,29∙log20,29 + 0,36∙log20,36)] = 31
H(S,U) = H(S) + H(U|S) = 1,674 + 1,638 = 32
= 3,312 (бит/два символа). ❒ 32
Таблица 2.1 38
Таблица 2.2 39
ΔI = L∙H(X|Y); (3.1) 49
где H(X|Y) – условная энтропия входного алфавита канала связи относительно выходного. 50
I = L∙H(Y) – ΔI = L[H(Y) – H(X|Y)]. (3.2) 50
где H(X,Y) – энтропия объединения входного X и выходного Y алфавитов; H(Y) – энтропия выходного алфавита Y. 50
Определим энтропию H(Y) выходного алфавита Y: 50
+ 0,001∙log20,001 + 0,099∙log20,099) = 2,069 (бит/два симв.). 52
Найдем условную энтропию входного алфавита относительно выходного: 52
Определим условную энтропию H(Y|X) выходного алфавита Y относительно входного X по формуле: 54
H(Y|X) = – [0,37∙(0,97∙log20,97 + 0,02∙log20,02 + 54
Таблица 3.1 60
Таблица 3.2 60
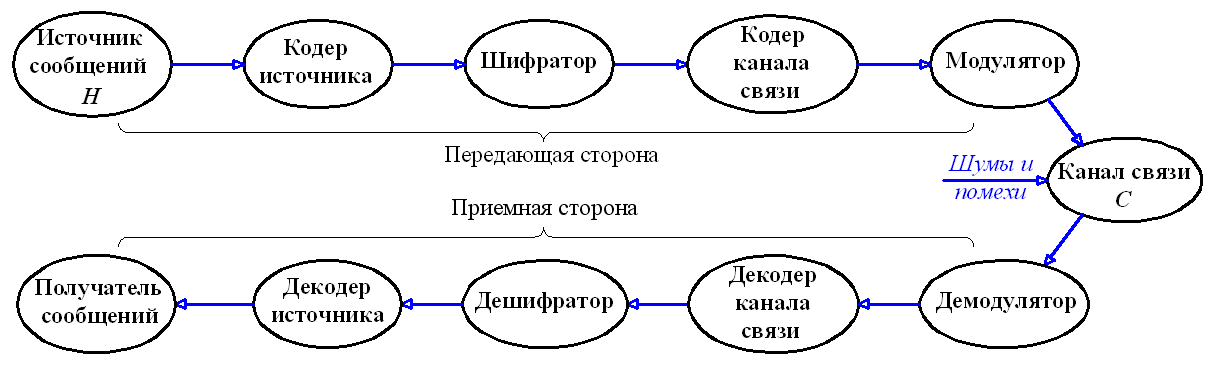
Для того чтобы эффективнее использовать канал связи (устройство хранения), следует так преобразовывать порожденную источником сообщений информацию, чтобы ее передача (хранение) сопровождалась наименьшими затратами. Такое преобразование информации называется кодированием источника сообщений. 62
При кодировании источника сообщений каждому символу алфавита S = {s1, s2, … , sm} источника соответствует последовательность символов алфавита X = {x1, x2, … , xK} кодера этого источника. Упорядоченная последовательность символов , соответствующая определенному символу si, называется кодовым словом. 62
Под кодом понимают множество всех кодовых слов {, … , }. 62
Средней длиной кодовых слов называется величина: 62
Рис. 4.2. Кодовое дерево для кода Хаффмана 67
Таблица 4.3 68
Рис. 5.2. Графическая интерпретация арифметического кодирования последовательности 75
Требуется выполнить декодирование арифметического кода = 100010101, полученного в примере 5.1. Процесс декодирования представлен в таблице 5.2. 75
Отсюда последовательность символов, полученная путем декодирования арифметического кода, будет s2s3s2s1s2, что полностью совпадает с данными из примера 5.1. ❒ 76
SkSk-1...S2S1, 87
S1 = х1 х3 х5 х7 ... = 0, 87
S2 = х2 х3 х6 х7 ... = 0, 87
Так 87
= 011111. 88
S1 = х1 х3 х5 х7 х9 = 0; 88
S1 = х1 0 1 1 1 = х1 1 = 0. 88
S2 = х2 х3 х6 х7 х10 = 0; 88
S2 = х2 0 1 1 1 = х2 1 = 0. 88
S3 = х4 1 1 1 = х4 1 = 0. 88
S4 = х8 х9 х10 = 0; 89
S4 = х8 1 1 = х8 0. 89
SkSk-1...S2S1, = 00...00, 89
Таблица 7.1 97
Таблица 5.3 106
Таблица 6.3 111
Таблица П.1 119
Таблица П.2 119
Примечание. 120