Интегро-дифференцирующее звено:

%Изучение типовых динамических звеньев: интегро дифференцирующее звено

%

%Очистка всех переменных в памЯти

clearall

%Очистка командного окна

clc

%Закрытие всех предыдущих рисунков

set(0,'ShowHiddenHandles','on')

delete(get(0,'Children'))

%Описание интегро дифференцирующего звена (N_zv = 4) через

%его передаточную функцию

%при различных значениЯх параметров. Параметры интегро дифференцирующего звена

%задаютсЯ вектором inp_param = [T1,T2] (см. текст файла TF_zv.m)

%изменЯем T1

W_11 = TF_zv(2,[2.05,4.1]);

W_12 = TF_zv(2,[4.1,4.1]);

W_13 = TF_zv(2,[8.2,4.1]);

%изменЯем Т2

W_21 = TF_zv(2,[4.1,2.05]);

W_22 = TF_zv(2,[4.1,4.1]);

W_23 = TF_zv(2,[4.1,8.2]);

%Построение требуемых характеристик при различных T1

%ЛАЧХ и ЛФЧХ

ltiview({'bode'},W_11,'b-',W_12,'r-',W_13,'k-')

%АФХ

ltiview({'nyquist'},W_11,'b-',W_12,'r-',W_13,'k-')

%весоваЯфункциЯ w(t)

ltiview({'impulse'},W_11,'b-',W_12,'r-',W_13,'k-')

%переходнаЯфункциЯ h(t)

ltiview({'step'},W_11,'b-',W_12,'r-',W_13,'k-')

%Построение требуемых характеристик при различных T2

%ЛАЧХ и ЛФЧХ

ltiview({'bode'},W_21,'b-',W_22,'r-',W_23,'k-')

%АФХ

ltiview({'nyquist'},W_21,'b-',W_22,'r-',W_23,'k-')

%весоваЯфункциЯ w(t)

ltiview({'impulse'},W_21,'b-',W_22,'r-',W_23,'k-')

%переходнаЯфункциЯ h(t)

ltiview({'step'},W_21,'b-',W_22,'r-',W_23,'k-')

При различных T₁ (2.05; 4.1; 8.2)T₂=T_баз

Рис.9 Переходная ф-я

Рис.11 ЛАЧХ и ЛФЧХ

Рис.10 Весовая ф-я

Рис.12 АФХ

Выводы:

1.При уменьшении значения параметра T1уменьшается начальное значение переходной функции; при T1 = Tбаз переходная функция представляет собой единичную функцию;

2.При уменьшении значения параметра T1 увеличивается начальное значение весовой функции; при T1 = Tбаз весовая функция обращается в 0 для любого 𝜔;

3.Для T2<T1: радиус АФХ уменьшается; Т1=Т2: АФХ – точка (-1,0i); T2>T1: радиус АФХ увеличивается. Т.к. мы рассматриваем только неотрицательные частоты, то нужной АФХ соответствуют значения только с неотрицательной мнимой частью для T2>T1 и наоборот для T2<T1

4.В области низких частот для различных значений T1 ЛАЧХ совпадают; в области средних и высоких частот чем больше параметр T1, тем большее значение принимают ЛАЧХ для одних и тех же значений частот; при T1 = TбазЛАЧХ обращается в 0 для любого 𝜔;

5.В области низких и высоких частот для различных значений T1 ФЧХ совпадают; в области средних частот чем больше параметр T1, тем большее значение принимают ФЧХ для одних и тех же значений частот; при T1 = TбазФЧХ обращается в 0 для любого 𝜔.

При различных T₂ (2.05; 4.1; 8.2)T₁=T_баз

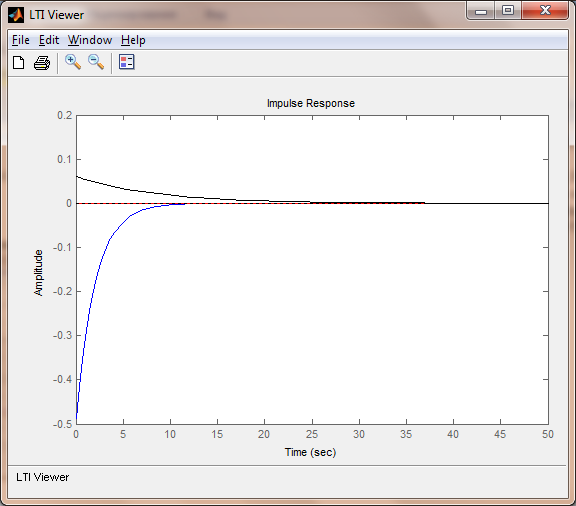
Рис.13 Переходная ф-я Рис.14 Весовая ф-я

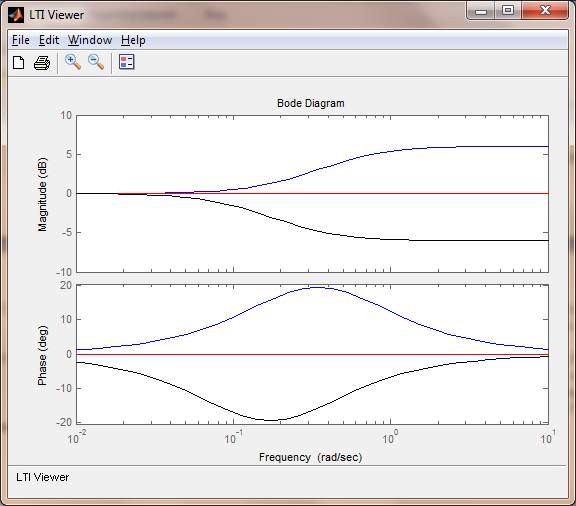
Рис.15 ЛАЧХ и ЛФЧХ Рис.16 АФХ

Вывод:

1.При уменьшении значения параметра T2уменьшается начальное значение переходной функции; при T2 = Tбаз переходная функция представляет собой единичную функцию;

2.При уменьшении значения параметра T2 увеличивается начальное значение весовой функции; при T2 = Tбаз весовая функция обращается в 0 для любого 𝜔;

3.Для T1<T2: радиус АФХ уменьшается; Т2=Т1: АФХ – точка (-1,0i); T1>T2: радиус АФХ увеличивается. Т.к. мы рассматриваем только неотрицательные частоты, то нужной АФХ соответствуют значения только с неотрицательной мнимой частью для T1>T2и наоборот для T1<T2

4.В области низких частот для различных значений T2 ЛАЧХ совпадают; в области средних и высоких частот чем больше параметр T2, тем меньшее значение принимают ЛАЧХ для одних и тех же значений частот; при T2 = TбазЛАЧХ обращается в 0 для любого 𝜔;

5.В области низких и высоких частот для различных значений T2 ФЧХ совпадают; в области средних частот чем больше параметр T2, тем меньшее значение принимают ФЧХ для одних и тех же значений частот; при T2 = TбазФЧХ обращается в 0 для любого 𝜔.