Вступ

З настанням двадцять першого століття людство не мислить себе без цифрових технологій. Цифрове телебачення, цифрова фото- й відеозйомка, цифровий стільниковий і стаціонарний зв'язок і т.д.; людина користується цими благами цивілізації, не замислюючись про те, як і що там працює. Але ж там відбуваються дуже складні дії над інформацією, представленою у двійковій системі числення.

Пристрої, які забезпечують цифрову обробку інформації, називаються цифровими. Ці пристрої виконані на цифрових інтегральних мікросхемах, що дозволяє значно зменшити габарити пристроїв, масу, споживану потужність, вартість і набагато поліпшити надійність. Застосування технологій великих і надвеликих інтегральних мікросхем дозволило перенести комп'ютери з лабораторій і спеціальних установ у кожен будинок. Крім поліпшення якості й надійності апаратури інтегральні мікросхеми також впливають на продуктивність й якість праці людини, за допомогою того, що робота стає автоматизованою отже, збільшується в рази обчислювальна здатність і зменшується ризик помилки.

З появою цифрових пристроїв у техніці зв'язку стало можливим надання величезної кількості послуг, покращилася якість зв'язку й збільшився обсяг передаваємої інформації.

Вершиною цифрової техніки є мікропроцесор. Мало хто знає, що в сучасних японських автомобілях автоматичним підкачуванням коліс управляє мікропроцесор.

Мікропроцесорні пристрої широко використовуються в апаратурі, що забезпечує обмін, обробку й розподіл інформації.

1 Проектування пристрою відображення символів на семисегментному індикаторі

1. Відображення символів у вигляді семисегментного індикатору

Семисегментний індикатор та зображення символів згідно варіанту завдання показані на рисунку 1.1 – 1.2

Рисунок 1.1 – Семисегментний індикатор

Рисунок 1.2 – Зображення символів у семисегментному індикаторі

2. Розробка таблиці істинності для сегментів індикатору

Згідно позначень сегментів на індикаторі та зображень символів на ньому, що показані на рисунку 1.1 – 1.2, складемо таблицю істинності для сегментів.

Таблиця 1.1 – Таблиця істинності для сегментів індикатору

№	Х1	Х2	Х3	Х4	a	b	c	d	e	f	g	Символ
0	0	0	0	0	1	0	1	1	0	1	1	0
1	0	0	0	1	1	0	1	1	1	1	1	6
2	0	0	1	0	1	1	1	1	1	1	1	7
3	0	0	1	1	1	1	1	1	0	1	1	4
4	0	1	0	0	0	1	1	0	0	0	0	3
5	0	1	0	1	1	1	1	0	1	1	1	Ч
6	0	1	1	0	1	0	0	1	1	1	1	Ь
7	0	1	1	1	1	1	0	0	1	1	1	L

Продовження таблиці 1.1

№	Х1	Х2	Х3	Х4	a	b	c	d	e	f	g	Символ
8	1	0	0	0	1	0	0	0	1	1	1	F
9	1	0	0	1	1	1	0	1	1	1	1	e
10	1	0	1	0	—	—	—	—	—	—	—	—
11	1	0	1	1	—	—	—	—	—	—	—	—
12	1	1	0	0	—	—	—	—	—	—	—	—
13	1	1	0	1	—	—	—	—	—	—	—	—
14	1	1	1	0	—	—	—	—	—	—	—	—
15	1	1	1	1	—	—	—	—	—	—	—	—

1.3 Отримання мінімальної диз’юнктивної нормальної форми (МДНФ) функцій сегментів семисегментного індикатора та побудова комбінаційних схем, що реалізують ці функції, в заданому елементному базисі

За допомогою таблиці істинності згідно таблиці 1.1 та діаграм Вейча, що показані на рисунках 1.3 – 1.9 запишемо функції сегментів в мінімальній диз’юнктивній нормальній формі і переведемо функції в елементний базис АБО-НЕ за допомогою правил де Моргана.

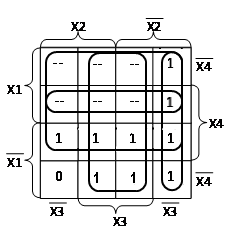
Рисунок 1.3 – Діаграма Вейча для сегмента “а”

Згідно рисунка 1.3 отримуємо МДНФ функції сегменту “а”.

(1.1)

Рисунок 1.4 – Діаграма Вейча для сегмента “b”

Згідно рисунка 1.4 отримуємо МДНФ функції сегменту “b”.

(1.2)

Рисунок 1.5 – Діаграма Вейча для сегмента “с”

Згідно рисунка 1.5 отримуємо МДНФ функції сегменту “с”.

(1.3)

Рисунок 1.6 – Діаграма Вейча для сегмента “d”

Згідно рисунка 1.6 отримуємо МДНФ функції сегменту “d”.

(1.4)

Рисунок 1.7 – Діаграма Вейча для сегмента “e”

Згідно рисунка 1.7 отримуємо МДНФ функції сегменту “е”.

(1.5)

Рисунок 1.8 – Діаграма Вейча для сегмента “f, g”

Згідно рисунка 1.8 отримуємо МДНФ функції сегменту “f, g”.

(1.6;1.7)

Накреслимо схеми для функцій сегментів в заданому базисі логічних елементів, представлених в МДНФ, що наведені у виразах 1.3 – 1.7.

Згідно виразу 1.1 будуємо комбінаційну схему, що реалізує МДНФ_а. Схема показана на рисунку 1.10.

Рисунок 1.10 – Комбінаційна схема, що реалізує МДНФ функції сегмента “а”

Згідно виразу 1.2 будуємо комбінаційну схему, що реалізує МДНФ_b. Схема показана на рисунку 1.11.

Рисунок 1.11 – Комбінаційна схема, що реалізує МДНФ функції сегмента “b”

Згідно виразу 1.3 будуємо комбінаційну схему, що реалізує МДНФ_c. Схема показана на рисунку 1.12.

Рисунок 1.12 – Комбінаційна схема, що реалізує МДНФ функції сегмента “c”

Згідно виразу 1.4 будуємо комбінаційну схему, що реалізує МДНФ_d. Схема показана на рисунку 1.13.

Рисунок 1.13 – Комбінаційна схема, що реалізує МДНФ функції сегмента “d”

Згідно виразу 1.5 будуємо комбінаційну схему, що реалізує МДНФ_e. Схема показана на рисунку 1.14.

Рисунок 1.14 – Комбінаційна схема, що реалізує МДНФ функції сегмента “e”

Згідно виразу 1.6 будуємо комбінаційну схему, що реалізує МДНФ_f,g. Схема показана на рисунку 1.15.

Рисунок 1.15 – Комбінаційна схема, що реалізує МДНФ функції сегмента “f, g”