БИЛЕТ №17

ВОПРОС№1

ИНТЕРФЕРЕНЦИЯ СВЕТА

План ответа:

1. Свет как электромагнитная волна.

2. Понятие интерференции.

3. Когерентность.

4. Интерференция света.

5. Условия наблюдения интерференции света.

6. Проявление интерференции света.

7. Применение интерференции света.

Свет как электромагнитная волна.

Современная оптика (раздел физики, который изучает свойства света, его физическую природу и взаимодействие с веществом) базируется на электромагнитной теории света.

Впервые, что свет представляет собой электромагнитную волну, сделал вывод шотландский физик Джеймс Максвелл в конце XIX века, который доказал существование электромагнитных волн.

После того, как немецкий физик Генрих Герц экспериментально получил электромагнитные волны и измерил их скорость, электромагнитная теория света получила своё первое подтверждение.

С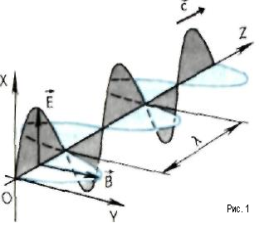 огласно электромагнитной теории света свет представляет собой электромагнитную волну.

Электромагнитной волной называется совокупность связанных друг с другом периодически изменяющих электрического и магнитного полей, распространяющихся с течением времени с конечной скоростью с (см. рис. 1).

Под изменением электрического и магнитного поля понимают изменение вектора напряжённости электрического поля и вектора магнитной индукции магнитного поля 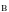. Если амплитуда колебаний вектора напряжённости электрического поля и вектора магнитной индукции магнитного поля с течением времени не изменяется, то такие колебания являются гармоническими и значения Е и В в любой момент времени определяются следующим образом:

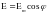
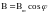
Величину φ, стоящую под знаком косинуса, называют фазой колебаний, описываемых этой функцией. Выражается фаза в угловых единицах – радианах. Фаза определяет значение напряжённости электрического поля Е и магнитной индукции магнитного поля В в любой момент времени.

Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах.

Электромагнитные волны являются поперечными – вектор скорости 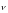, вектор напряжённости электрического поля и вектор индукции магнитного поля взаимно перпендикулярны (см. рис 1.).

То, что численное значение скорости света равно скорости распространения электромагнитной волны является одним из начальных подтверждений, что свет представляет собой электромагнитную волну.

Следующим доказательством того, что свет имеет волновую природу, явилось открытие английским учёным Томасом Юнгом явления интерференции света, которое присуще любому волновому процессу.

Понятие интерференции.

Так как интерференция присуща любому волновому процессу (в том числе и свету), то для пояснения сути этого явления рассмотрим его на примере механических волн.

Обычно в среде одновременно распространяется несколько различных волн. Если в некоторую точку пространства А приходят две монохроматические волны (монохроматические волны – волны с одинаковой частотой колебаний) от разных источников S₁ и S₂, то они возбуждают в ней гармонические колебания той же частоты (рисунок 2).

Пройдя различные геометрические пути r₁ и r₂, волны имеют разность хода Δr= r₂ –r₁. Если разность хода равна длине волны, то вторая волна запаздывает по сравнению с первой ровно на один период. Следовательно, в этом случае гребни (как и впадины) обеих волн совпадут. В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой (волны усиливают друг друга). То же самое будет происходить, если на отрезке Δr укладывается не одна, а любое целое число длин волн.

Рисунок 2

Вывод: амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн при условии, что фазы колебаний обоих источников совпадают (условие максимумов):

Δr = mλ, где m = 0,1,2,…

Если же на отрезке Δr = r₂ – r₁ укладывается половина длины волны, т.е. вторая волна отстаёт от первой на половину периода, то гребень одной волны совпадает с впадиной другой. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т.е. в рассматриваемой точке колебаний нет (рисунок 3).

В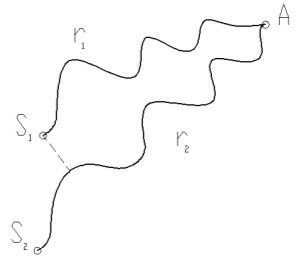 ывод: амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждаемых колебанием в этой точке, равна нечётному числу длин полуволн при условии, что фазы колебаний обоих источников совпадают (условие минимумов):

Δr = (2m + 1)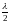 , где m = 0,1,2,…

Рисунок 3

Явление сложения в пространстве двух или более когерентных волн, при котором образуется постоянное во времени распределение амплитуд результирующего колебания (устойчивая картина чередующихся максимумов и минимумов амплитуд), называется интерференцией.

Интерференция волн возможна только при выполнении условия когерентности.

Когерентность.

Когерентностью называется явление согласованного протекания в пространстве и во времени нескольких колебательных (волновых) процессов. Колебания (волны) с одинаковой частотой и постоянной во времени разностью фаз называются когерентными.

Интерференция света.

Прежде, чем рассмотреть интерференцию света, необходимо ввести понятие оптической разности хода.

Рисунок 4

С учётом того, что скорость распространения световых волн в различных средах разная, в условиях максимума и минимума механических волн вместо понятия разность хода Δr (которое называется геометрической разностью хода) используют понятие оптическая разность хода Δ, которая равна:

Δ = n₂r₂ – n₁r₁,

где n₁ и n₂ абсолютные показатели преломления первой и второй среды соответственно (рисунок 4).

Произведение nr называется оптической длиной пути волны.

Первый демонстрационный эксперимент по наблюдению интерференции света был выполнен в 1802 году англичанином Томасом Юнгом. Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников.

В классической интерференционной схеме (схеме Юнга) перед экраном размещалась ширма, в которой имелись две, близкорасположенные щели S₁ и S₂. Эти щели освещались солнечным светом от одного источника S. Вместо двух ярких точек он наблюдал серию чередующихся тёмных или светлых колец (усиление или ослабление результирующих колебаний световой волны).

Объяснил наблюдаемое явление Томас Юнг следующим образом: единая световая волна pазбивается на две, идущие от pазличных щелей (см. рис. 5). Эти щели в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн. Вторичные волны когеpентны между собой и пpи наложении дpуг на дpуга дают систему максимумов и минимумов интенсивности света в виде темных и светлых полос соответствующего цвета.

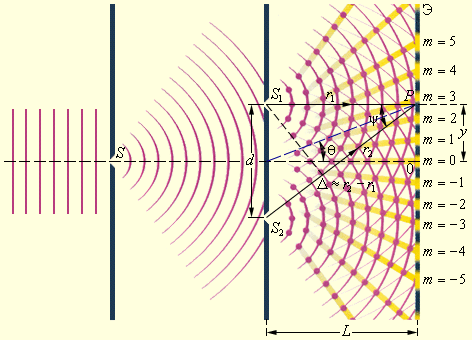
Рисунок 5

Где возникнет максимум и где минимум? Пpоведём от щелей, как от втоpичных когеpентных источников, лучи, сходящиеся в одной точке Р. Найдем pазность хода этих лучей - отpезок Δ = r₂ – r_1. Если на нём укладывается чётное число полуволн (волны приходят в одной фазе), то волны от щелей в точке P будут усиливать друг друга, и в указанной точке будет наблюдаться максимум. Если на отpезке Δ укладывается нечётное число полуволн (волны приходят в противофазе), то они будут гасить друг друга, и в точке P будет наблюдаться минимум интерференции. Таким обpазом, условия при которых возникают интерференционные максимумы и минимумы для световых волн, остаются соответственно такими же как и для механических волн:

Δr = mλ (условие максимума интерференции света);

Δr = (2m + 1) (условие минимума интерференции света),

где m = 0, 1, 2, …