Лабораторная работа №4 Определение ускорения свобо дного падения математическим маятником

Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости. Маятником, близким к математическому, может служить небольшой тяжелый шарик, совершающий колебания на бифилярном подвесе.

Если маятник вывести из положения равновесия, то относительно оси качания О возникает вращательный момент (см. рис.), численно равный 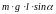, стремящийся возвратить маятник в положение равновесия (α = 0).

В соответствии с основным законом динамики вращательного движения, уравнение движения математического маятника имеет вид:

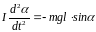, (1)

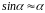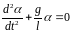где I – момент инерции маятника, α – угол отклонения маятника от положения равновесия, l – расстояние от центра тяжести шарика до оси качания. При малых колебаниях маятника . Тогда уравнение движения маятника примет вид: или , (2)

где I = ml² – момент инерции материальной точки.

Уравнение (2) является дифференциальным уравнением гармонических колебаний. Согласно теории гармонических колебаний период колебаний Т математического маятника определяется по формуле:

, (3)

из которой следует, что ускорение свободного падения g равно

. (4)

Для определения g по формуле (4) необходимо измерить период полного колебания маятника Т и его длину ℓ. Однако, непосредственное измерение длины маятника представляет сложную задачу, так как приходится определять центр тяжести, который при неоднородности материала шарика и неточности шаровой поверхности нелегко найти. Чтобы обойти эту трудность, в настоящей работе пользуются маятником переменной длины.

Наматывая нить, на которой подвешен маятник на небольшой блок, прикрепленный к стойке А, меняют длину маятника и проделывают 2 опыта с длинами ℓ₁ и ℓ₂.

Для каждого опыта согласно формуле (3) имеем

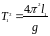и ,

откуда следует

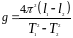. (5)

Разность длин легко найти как разность отсчетов положения рейки В, расположенной по касательной к шарику в том и другом случае.

Лабораторная работа №5 Определение коэффициента вязкости жидкости

При движении жидкости между ее слоями возникают силы внутреннего трения противостоящие «сдвигу» слоев, действующие таким образом, чтобы уровнять скорости всех слоев. Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному слою некоторый импульс, что приводит к торможению последнего.

Сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения ∆S и градиенту скорости 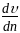в направлении внешней нормали n к поверхности слоя:

. (1)

Величина η называется коэффициентом внутреннего трения или вязкости. Коэффициент вязкости зависит от природы жидкости и для данной жидкости с повышением температуры вязкость уменьшается.

При падении шарика в вязкой жидкости на него действуют три силы:

1. Сила тяжести 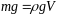(V - объем и ρ - плотность шарика)

2. Выталкивающая сила Архимеда 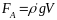(ρ^’ – плотность жидкости)

3. Сила внутреннего трения, действующая на шарик радиуса r при его медленном поступательном движении со скоростью  и тормозящая движение шарика, которая определяется по формуле Стокса .

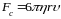На основании второго закона Ньютона имеем:

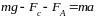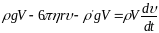или (2)

Вначале скорость движения шарика возрастает , но так как по мере увеличения скорости сила сопротивления так же возрастает, наступает такой момент, когда сила тяжести уравновешивается суммой сил Архимеда и Стокса и равнодействующая всех сил становится равной нулю.

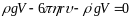. (3)

С этого момента движение шарика становится практически равномерным со скоростью 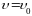. Решая уравнение движения относительно 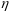, получим для коэффициента вязкости:

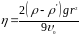. (4)

Скорость равномерного движения шарика 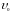можно определить, зная расстояние ℓ между метками на сосуде и время t, за которое шарик проходит это расстояние .

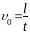Учитывая, что на опыте измеряется диаметр шарика, а не его радиус получаем расчетную формулу:

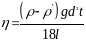. (5)