30.Передаточная функция разомкнутой системы.

Рассмотрим сначала ос­новной случай - отрицательную обратную связь.

На рисунке 3. изображена струк­турная схема замкнутой системы автоматического управления в наиболее общем виде, где G(р) и Z(р) - передаточные функции соответственно прямой цепи системы и цепи обратной связи. Сигнал обратной связи Х_o.с(р) вы­читается из входного сигнала Х_вх(р) (в случае положительной обратной связи они не вычитаются, а складываются). Переда­точные функции G(р) и Z(р) могут соответствовать как про­стым звеньям направленного действия, так и их любым комби­нациям.

Рисунок 3 - Параллельное встречное включение звеньев, направленного действия (обратная связь)

Для схемы, изображенной на рисунке 3

Исключив из них промежуточную величину Х_о.с, получим пе­редаточную функцию замкнутой системы

(5)

Где (6)

есть передаточная функция разомкнутой системы. Смысл по­следнего названия становится понятным, если мысленно разомк­нуть контур управления в любом месте и, «выпрямив» его, рас­сматривать прохождение сигнала, поданного в месте размыка­ния, по цепочке последовательно включенных звеньев направ­ленного действия.

31.Передаточная функция замк­нутой системы по входному воздействию.

Рассмотрим сначала ос­новной случай - отрицательную обратную связь.

На рисунке 3. изображена струк­турная схема замкнутой системы автоматического управления в наиболее общем виде, где G(р) и Z(р) - передаточные функции соответственно прямой цепи системы и цепи обратной связи. Сигнал обратной связи Х_o.с(р) вы­читается из входного сигнала Х_вх(р) (в случае положительной обратной связи они не вычитаются, а складываются). Переда­точные функции G(р) и Z(р) могут соответствовать как про­стым звеньям направленного действия, так и их любым комби­нациям.

Рисунок 3 - Параллельное встречное включение звеньев, направленного действия (обратная связь)

Для схемы, изображенной на рисунке 3

Исключив из них промежуточную величину Х_о.с, получим пе­редаточную функцию замкнутой системы

(5)

Итак, передаточная функция замкнутой системы автоматиче­ского управления равняется отношению передаточной функции прямой цепи к увеличенной на единицу передаточной функции разомкнутой системы.

Следует отметить, что этот вывод, равно как и формула (5), справедливы только для изображенного на рисунке 3 случая, ког­да внешнее воздействие поступает на вход системы управления. Поэтому Ф(р) иногда называют передаточной функцией замк­нутой системы по входному воздействию.

32.Структурные схемы сар напряжения генератора постоянного тока.

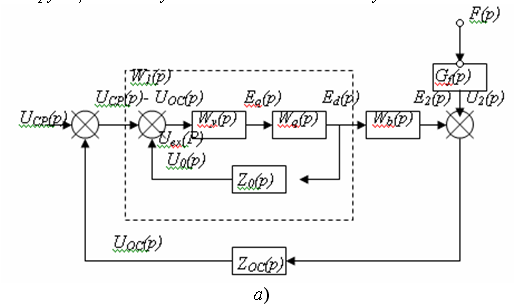
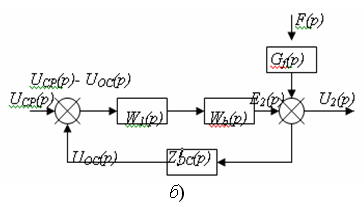
Рисунок 1 - Структурные схемы САР напряжения генератора постоянного тока, а – первоначальная, б – преобразованная.

Преобразование многоконтурных структурных схем с пере­крещивающимися связями производят по способу переключения (перенесения) связей, сущность которого поясняется на приме­ре, рисунок 1.

33. Преобразование Лапласа в применении к теории автоматического регулирования

При исследовании и расчетах систем автоматики ши­роко используется математический метод - преобразо­вание Лапласа.

Основанием для этого служит то обстоятельство, что такое преобразование существенно облегчает исследова­ние сложных систем, заменяя дифференциальные урав­нения алгебраическими. В частности, при решении диф­ференциальных уравнений систем преобразование Лап­ласа позволяет легко учитывать начальные условия и избежать сложных выкладок, связанных с вычислением постоянных интегрирования. Достаточно просто реша­ются также неоднородные уравнения, позволяющие учи­тывать влияние возмущений (записанных в правой ча­сти уравнения) на динамику процессов. Некоторые по­нятия, касающиеся обычного преобразования Лапласа и используемые при исследовании систем автоматики, приводятся ниже, а также в последующих главах.

Преобразование Лапласа преобразует функцию ве­щественного переменного (в том числе времени) в функ­цию комплексного переменного. Такое преобразование превращает дифференциальные уравнения в алгебраи­ческие, что дает определенные преимущества при реше­нии ряда задач.

Распространенное в теории САР понятие так назы­ваемой передаточной функции также использует понятие лапласова изображения.

Общее представление о прямом и обратном преобразованиях Лапласа. Если имеется некоторая функция ƒ(t) независимой вещественной переменной t (обычно времени), то пре­образование Лапласа, производимое над функцией ƒ(t) и обращающее ее в функцию F(р), определяется соот­ношением

(1)

здесь р - произвольная комплексная величина, обозна­чаемая , где σ и ω - вещественные переменные.

Функциональное преобразование вида (1), осуще­ствляемое над функцией ƒ(t), часто сокращенно обозна­чается так (2)

Функция ƒ(t) называется оригиналом, а функция F(р) - изображением функции ƒ(t).

Следует заметить, что при применении преобразова­ния Лапласа к функции ƒ(t) рассматриваются значения этой функции лишь при t>0, т. е. в технических зада­чах после приложения к системе внешних возмущающих воздействий, а именно это и представляет практический интерес при решении задач автоматического регулиро­вания.

Для того чтобы преобразованная функция была опре­делена, достаточно потребовать, чтобы интеграл (5.1) существовал для некоторой области р, за пределами ко­торой этот интеграл может и не иметь смысла. Так, например, изображение оригинала, равного еди­нице, т. е. если ƒ(t) = [1], будет равно Здесь при вычислении интеграла предполагается, что ве­щественная часть р положительна (σ>0). При σ≤0 ин­теграл не существует, но преобразованная функция от единицы всегда равняется 1/р.

Может случиться, что интеграл (5.1) не существует ни при каких значениях р. В этом случае преобразова­ние (2) невозможно. Однако в физических задачах, описываемых дифференциальными уравнениями в пол­ных производных с постоянными коэффициентами, и при обычном типе возмущающих воздействий это преобра­зование всегда осуществимо.

Наряду с прямым преобразованием (1) функции времени ƒ(t) в F(р), т. е. наряду с операцией перехода от функции вещественного переменного t к функции ком­плексного переменного р, пользуются обратным преоб­разованием, т. е. преобразованием изображения в ори­гинал. При этом производится обратная операция опре­деления оригинала ƒ(t) по заданному изображению F(р). Эта операция обозначается символом L^-1 или 1/L. Таким образом, в этом случае имеем (3) При этом преобразовании теорема о начальном значе­нии функции ƒ(t) записывается так а теорема о конечном значении

Нахождение лапласова изображения для линейного дифференциального уравнения. Положим, что линейная система автоматического ре­гулирования описывается дифференциальным уравнением n-го порядка с постоянными коэффициентами следу­ющего вида (4)

Умножая левую и правую части уравнения (4) на е^-pt и интегрируя в пределах от 0 до ∞, получим

Воспользовавшись вышеприведенными обозначениями, пра­вилами о преобразованиях Лапласа, можно написать Полагая, что система находится при нулевых начальных условиях и зная лапласово изображение для производ­ных, для данного случая получим (5)

Или

(6)

Выражение (6) является лапласовым изображением дифференциального уравнения (4) при нулевых начальных условиях.