25. Основные способы включения звеньев сау.

Рассмотрим основные случаи включения звеньев направлен­ного действия.

Последовательное включение (одноконтурная разомкнутая система). Структурная схема приведена на рисунке 1.

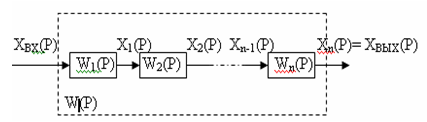
Рисунок 1 - Последовательное включение звеньев

направленного действия

Для каждого из п звеньев мож­но записать

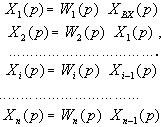(1)

Исключая все промежуточные величины, т. е. подставляя предыдущие в последующие, получим выражение для последне­го члена

Учитывая, что выход последнего n-го звена является одновре­менно выходной величиной системы, т. е.

получим

₍₂₎

Так как отношение по определению есть передаточная функция всей системы то окончательно будем иметь (3)

Итак, передаточная функция последовательно включенных звеньев равняется произведению пере­даточных функций от­дельных звеньев.

Параллельное, согласное включе­ние. Параллельным со­гласным включением зве­ньев направленного дей­ствия считается такое, при котором входная ве­личина системы подается параллельно на входы всех звеньев, а их выход­ные величины алгебраически суммируются на выходе системы. На рисунке 2 изображен частный случай параллельного соглас­ного включения трех звеньев направленного действия.

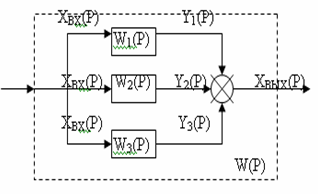
Рисунок 2 - Параллельное согласное вклю­чение

звеньев направленного действия

На основании формулы (2) для каждого из п параллельно, включенных звеньев можно записать

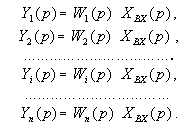
Суммируя написанные равенства и принимая во внимание, что по определению параллельного согласного включения, звень­ев направленного действия сумма левых частей является выход­ной величиной системы, получим

Согласно определению передаточной функции (1), из по­следнего выражения будем иметь

(4)

Таким образом, передаточная функция параллельных соглас­но включенных звеньев направленного действия равняется алге­браической сумме передаточных функций отдельных звеньев.

Параллельное встреч­ное включение (обратная связь). Рассмотрим сначала ос­новной случай - отрицательную обратную связь.

На рисунке 3. изображена струк­турная схема замкнутой системы автоматического управления в наиболее общем виде, где G(р) и Z(р) - передаточные функции соответственно прямой цепи системы и цепи обратной связи. Сигнал обратной связи Х_o.с(р) вы­читается из входного сигнала Х_вх(р) (в случае положительной обратной связи они не вычитаются, а складываются). Переда­точные функции G(р) и Z(р) могут соответствовать как про­стым звеньям направленного действия, так и их любым комби­нациям.

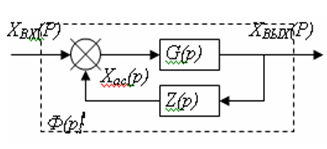
Рисунок 3 - Параллельное встречное включение звеньев, направленного действия (обратная связь)

Для схемы, изображенной на рисунке 3

Исключив из них промежуточную величину Х_о.с, получим пе­редаточную функцию замкнутой системы

(5)

Где (6)

есть передаточная функция разомкнутой системы. Смысл по­следнего названия становится понятным, если мысленно разомк­нуть контур управления в любом месте и, «выпрямив» его, рас­сматривать прохождение сигнала, поданного в месте размыка­ния, по цепочке последовательно включенных звеньев направ­ленного действия.

Итак, передаточная функция замкнутой системы автоматиче­ского управления равняется отношению передаточной функции прямой цепи к увеличенной на единицу передаточной функции разомкнутой системы.

Следует отметить, что этот вывод, равно как и формула (5), справедливы только для изображенного на рисунке 3 случая, ког­да внешнее воздействие поступает на вход системы управления. Поэтому Ф(р) иногда называют передаточной функцией замк­нутой системы по входному воздействию.