1.Функциональные схемы систем автоматического управления

Любой технологический процесс, протекающий в какой-либо установке, машине, двигателе, т. е. в самых разнообразных объектах, можно характеризовать одним или несколькими показателями процесса. Такими показателями могут быть самые различные физические, химические и другие величины. Такие показатели процесса называют также параметрами процесса (координатами процесса, величинами про­цесса).

Обеспечение всего комплекса возможных операций по управлению объектом без участия обслуживающего персонала выполняется системой автомати­ческого управления (САУ). Обеспечение же только требуемых значений параме­тров, определяющих желаемый ход технологического процесса в том или ином объекте без участия человека, осуществляется устройством автоматического регулирования.

Параметры объекта, которые подлежат изменению или стабилизации, принято называть регулируемы­ми параметрами, а объект, в котором регулируются такие параметры, называют объектом регулирования.

Сказанное выше можно также сформулировать так: устройства, предназначенные для автоматического под­держания постоянного значения регулируемых параме­тров в разнообразных объектах или изменяющие регулируемые параметры по какому-либо требуемому зако­ну, называют автоматическими регуляторами. Сочетание объекта регулирования с автоматическим регулятором принято называть системой автома­тического регулирования (САР), которая является частным случаем САУ. Любую систему регулирования можно разложить на ряд эле­ментов.

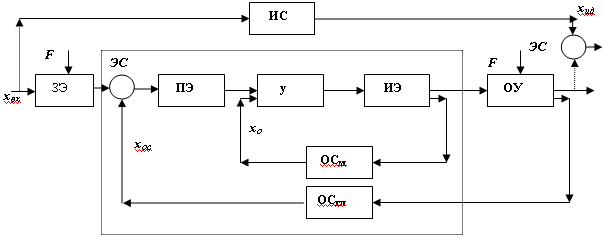
Рисунок 1.1 - Общая функциональная схема САУ

Как видно из схемы (рисунок 1.1), на объект управления ОУ (называемый также объектом регулирования ОР), находящий­ся под влиянием внешнего возмущающего воздействия F, посту­пает регулирующее воздействие х_р, являющееся выходной вели­чиной управляющей части системы (регулятора), которая пред­ставляет собой совокупность обведенных пунктиром элементов, специально введенных для получения замкнутой системы авто­матического управления (регулирования).

Замыкание контура управления производится подачей в ре­гулятор по цепи главной обратной связи ОС_ГЛ управляемой ве­личины, которая в общем случае может отличаться от выходной величины объекта управления, если последняя недоступна для прямого контроля (например, измерение тока якоря электродви­гателя вместо непосредственного контролирования вращающего момента, противо-э.д.с. вместо скорости вращения якоря и т.д.). При этом ошибка системы определяется разно­стью между действительной выходной величиной х_вых и ее «иде­альным» значением х_к%, представляющим собой выход некото­рой воображаемой «идеальной» системы ИС, осуществляющей точное заданное преобразование входной величины. Необходимость введения задающего элемента ЗЭ объясняет­ся тем, что задающее воздействие, непосредственно поступаю­щее на элемент сравнения ЭС, может отличаться от входной ве­личины по двум причинам:

а) эти воздействия могут быть связа­ны друг с другом определенной функциональной зависимостью * или просто различаться масштабом величин;

б) задающее воздействие часто содержит в себе, наряду с полезным входным сигналом, и случайные возмущения или помеху (шум).

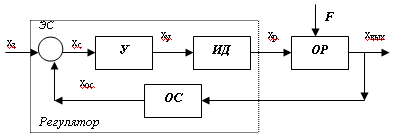
Рисунок 1.2 - Функциональная схема простейшей системы автоматического регулирования

Сигнал ошибки х_с, представляющий собой разность задаю­щего воздействия х_з и сигнала главной обратной связи х_о.с, в об­щем случае не должен отождествляться с ошибкой ∆х, даже ес­ли выходная величина совпадает с управляемой, а задающее воздействие — с входной величиной. Так, в статической системе при отсутствии возмущающих воздействий и неизменных пара­метрах системы установившаяся ошибка равна нулю, при этом сигнал ошибки должен иметь отличную от нуля величину, необ­ходимую для поддержания заданного значения выходной вели­чины системы.

Усилительный элемент У и исполнительный элемент ИЭ вхо­дят в основной контур системы. Преобразующий элемент ПЭ и элемент местной обратной связи ОС_м вводятся в систему для придания ей лучших динами­ческих свойств, т. е. для коррекции системы, в связи с чем их на­зывают соответственно последовательным и параллельным кор­ректирующими элементами. Их наличие не является обязатель­ным. Однако в этом случае могут быть осуществлены лишь про­стейшие САУ с крайне низкими качественными показателями.

Рисунок 1.3 – Функциональная схема простейшей следящей системы

На рисунке 1.2 и 1.3 изображены соответственно функциональ­ные схемы простейшей замкнутой САР и простейшей следящей системы. Особенностью этих схем является то, что все изображенные на них элементы являются необходимыми. Отсутствие какого-либо из них делает невозможным существование замкнутой системы автоматическо­го управления. В обеих системах предполагается возможность непосредственного контролирования выходной величины (которая совпадает с уп­равляемой или регулиру­емой величиной) и совпа­дение задающего воздей­ствия с входом системы. На практике это имеет место тогда, когда существует твердая уверенность в том, что указанные пары величин связаны между собой жесткой зависи­мостью (обычно пропорциональной).

Особенностью следящих систем, предназначенных для отра­ботки (отслеживания) механических перемещений, является, как правило, высокая точность передачи сигнала по цепи глав­ной обратной связи ОС_ГЛ от выхода системы к элементу срав­нения ЭС. При этом в установившемся режиме выходная величина θ_вых должна с очень малой (по сравнению с переходным режимом) погрешностью совпадать с входной величиной θ_вх*. Вследствие этого элемент главной обратной связи производит передачу сигнала к элементу сравнения с коэффициентом, рав­ным единице, и может быть заменен на функциональной схеме одной линией (рисунок 1.3). При этом ошибка следящей системы θ = θ_вх - θ_вых.