
- •1. Зміст дисципліни
- •1.1. Механіка
- •2. Рекомендована література
- •2.1. Основна література
- •2.2. Додаткова література
- •3. Теоретичний матеріал, знання якого необхідне для успішного виконання роботи
- •3.1. Кінематика матеріальної точки
- •Миттєва швидкість частинки: ,
- •3.2. Динаміка матеріальної точки
- •3.3. Сили тертя. Пружні сили. Закон всесвітнього тяжіння.
- •3.4. Механіка твердого тіла
- •3.5. Робота сили. Потужність. Закони збереження
- •Аналогія між поступальним та обертальним рухами
- •3.6. Механіка рідин і газів
- •3.7. Рух тіл в неінерціальних системах відліку
- •3.8. Елементи спеціальної теорії відносності (ств)
- •3.9. Механічні коливання і хвилі. Елементи акустики
- •4. Приклади розв’язування задач
- •5. Розподіл задач за варіантами
- •6. Задачі для контрольної роботи
- •7. Таблиці основних фізичних величин Основні фізичні константи
- •Деякі астрономічні величини
- •Пружні властивості матеріалів
- •Коефіцієнти тертя ковзання
- •Швидкість поширення звукових хвиль,
- •Співвідношення між температурними шкалами
- •Коефіцієнти поверхневого натягу
- •Поверхневий натяг води при різних температурах
- •Питома теплота згоряння палива,
- •Діаметри деяких молекул,
- •Поправки Ван-дер-Ваальса
- •Критичні значення температури та тиску
- •Температура плавлення, температура кипіння, питома теплота плавлення, питома теплота пароутворення
- •Значення синусів і тангенсів
6. Задачі для контрольної роботи
Три четверті свого шляху автомобіль проїхав зі швидкістю
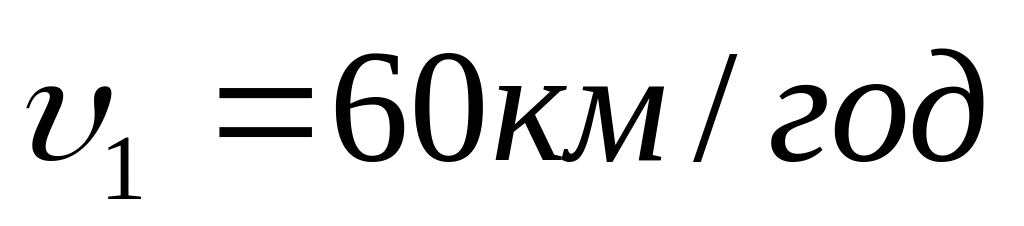 ,
іншу частину шляху – зі швидкістю
,
іншу частину шляху – зі швидкістю
 .
Яка середня шляхова швидкість
.
Яка середня шляхова швидкість
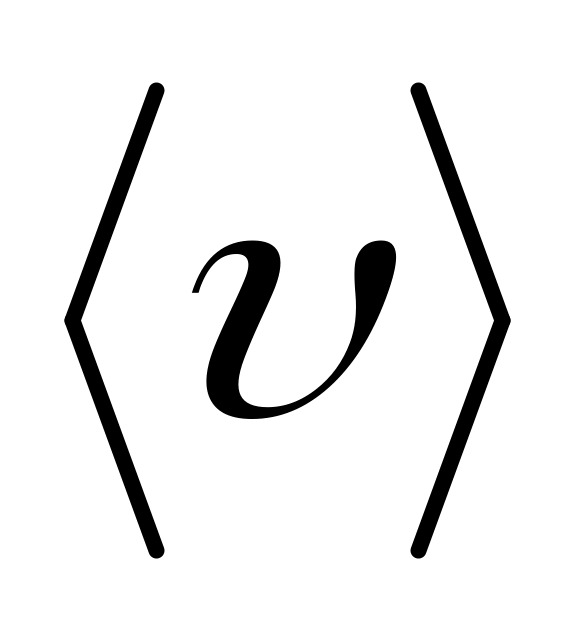 руху автомобіля?
руху автомобіля?
Рівняння прямолінійного руху має вигляд
 ,
де
,
де

 .
Побудуйте графіки залежності координати
і шляху від часу для заданого руху.
.
Побудуйте графіки залежності координати
і шляху від часу для заданого руху.
Рух матеріальної точки задано рівнянням , де
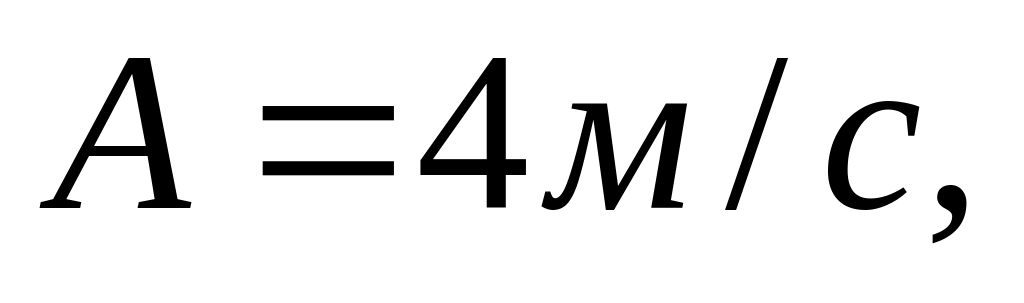
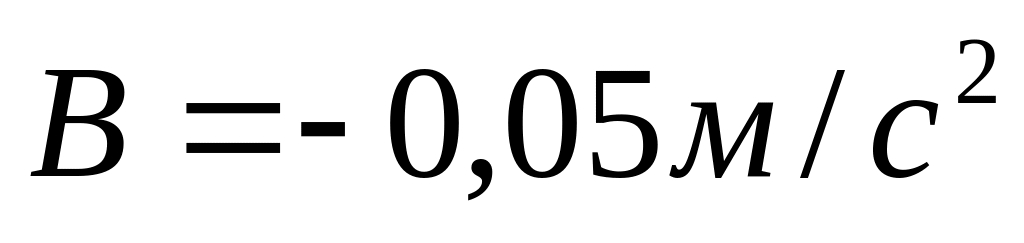 .
Визначте момент часу, в якому швидкість
точки рівна нулю. Знайти координату і
прискорення в цей момент. Побудуйте
графіки залежності координати, шляху,
швидкості і прискорення цього руху від
часу.
.
Визначте момент часу, в якому швидкість
точки рівна нулю. Знайти координату і
прискорення в цей момент. Побудуйте
графіки залежності координати, шляху,
швидкості і прискорення цього руху від
часу.
Рух двох матеріальних точок задано рівняннями:

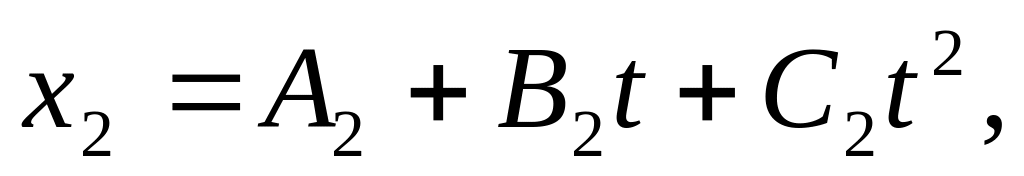 де
де
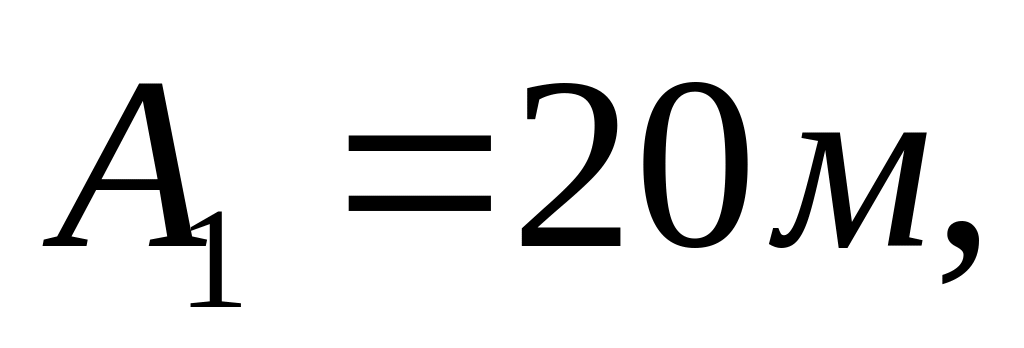
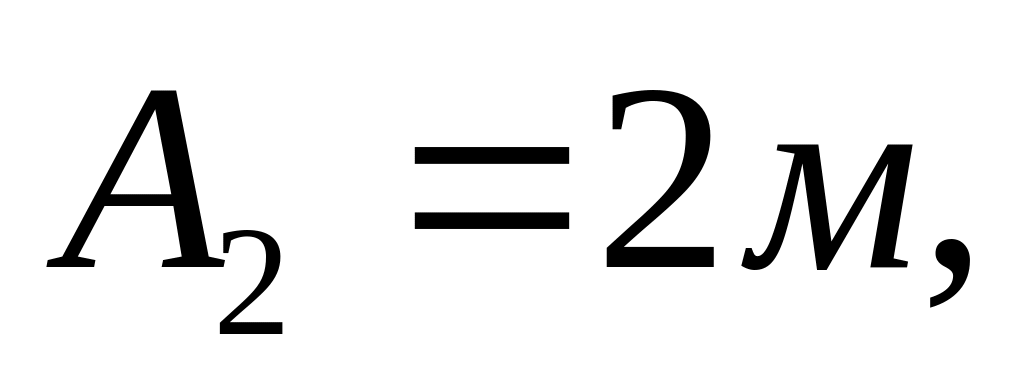
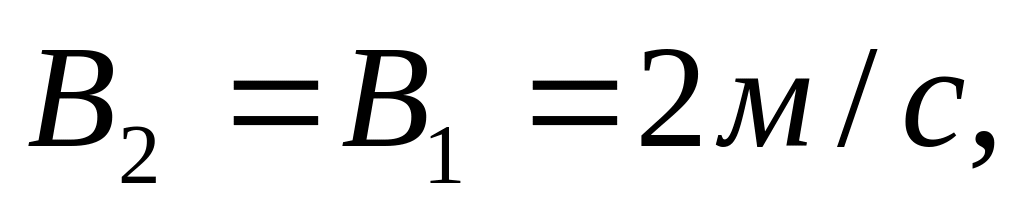

 В який момент часу
швидкості цих точок будуть однаковими?
Визначте швидкості
В який момент часу
швидкості цих точок будуть однаковими?
Визначте швидкості
 і
і
 та
прискорення
та
прискорення
 і
і
 точок
в цей момент часу.
точок
в цей момент часу.
Дві матеріальні точки рухаються згідно з рівнянням:

 де
де




 В який момент часу
прискорення
цих точок буде однаковим? Знайти
швидкості
і
точок в цей момент.
В який момент часу
прискорення
цих точок буде однаковим? Знайти
швидкості
і
точок в цей момент.
Камінь падає з висоти
 Який шлях
Який шлях
 пройде камінь за останню секунду свого
падіння?
пройде камінь за останню секунду свого
падіння?
Камінь кинутий вертикально вгору з початковою швидкість
 .
Через який час камінь буде знаходиться
на висоті
.
Через який час камінь буде знаходиться
на висоті
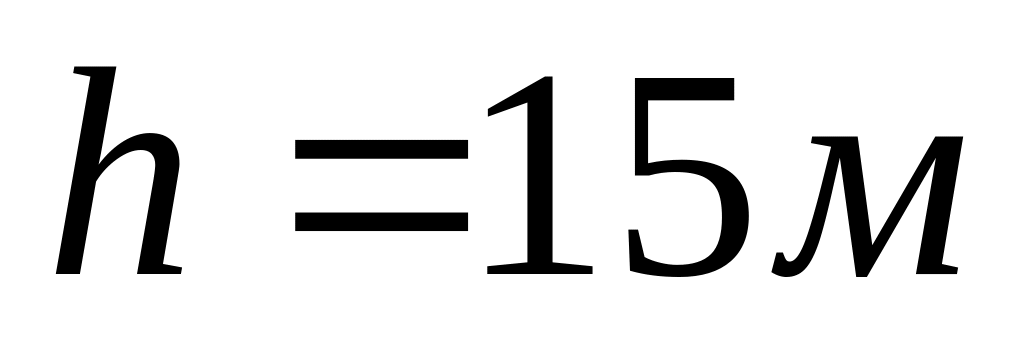 ?
Знайти швидкість
каменя на цій висоті. Опором повітря
знехтувати. Прийняти
?
Знайти швидкість
каменя на цій висоті. Опором повітря
знехтувати. Прийняти
 .
.
Тіло, кинуте вертикально вгору, знаходилось на одній і тій же висоті
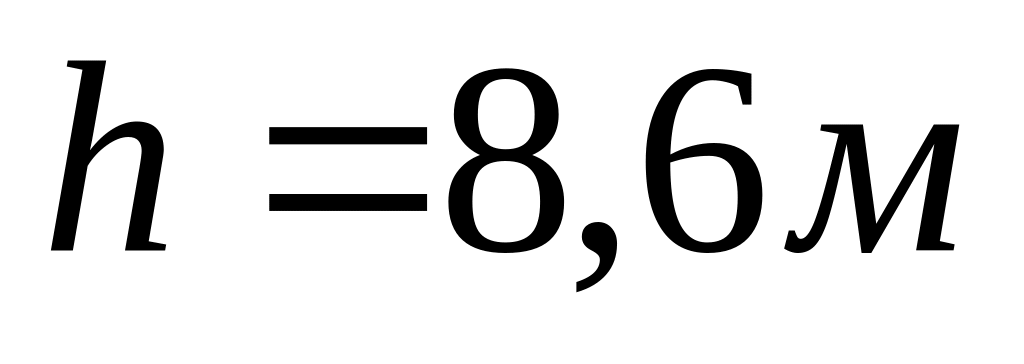 два рази з інтервалом
два рази з інтервалом
 .
Нехтуючи опором руху, визначити початкову
швидкість кинутого тіла.
.
Нехтуючи опором руху, визначити початкову
швидкість кинутого тіла.
З балкону кинули м’яч вертикально вгору з початковою швидкістю
 .
Через
.
Через
 м’яч упав на землю. Визначити висоту
балкона над землею і швидкість м’яча
в момент удару об землю.
м’яч упав на землю. Визначити висоту
балкона над землею і швидкість м’яча
в момент удару об землю.
Точка рухається по прямій згідно рівняння:
 де
де
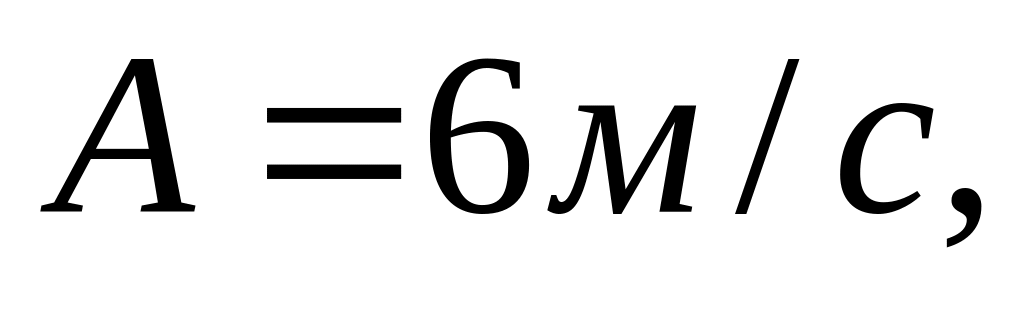
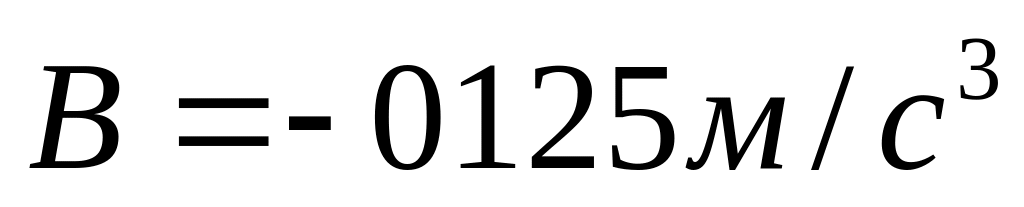 .
Визначити середню шляхову швидкість
точки в інтервалі часу від
.
Визначити середню шляхову швидкість
точки в інтервалі часу від
 до
до
 .
.
Матеріальна точка рухається по площині згідно рівняння:
 .
Написати залежності: 1)
.
Написати залежності: 1) 2)
2)
 .
.
Рух матеріальної точки задано рівнянням
 де
де


 .
Накреслити траєкторію точки. Найти
вирази
.
Накреслити траєкторію точки. Найти
вирази
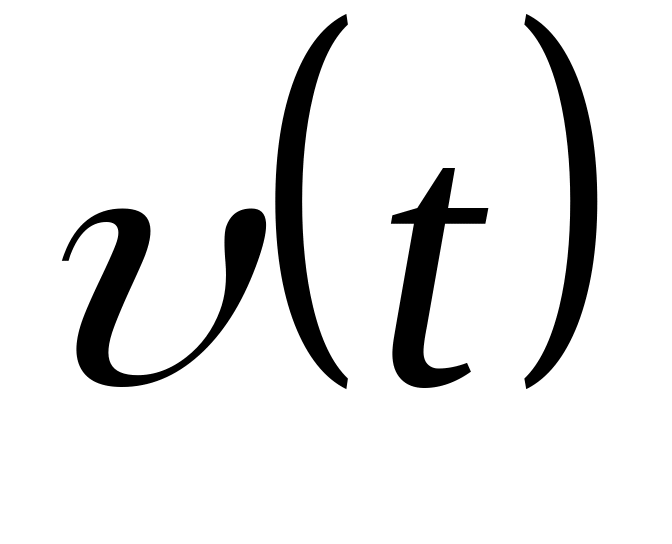 і
.
Для моменту часу
і
.
Для моменту часу
 обчислити: 1) модуль швидкості
обчислити: 1) модуль швидкості
 ;
2) модуль прискорення
;
2) модуль прискорення
 ;
3) модуль тангенціального прискорення
;
3) модуль тангенціального прискорення
 ;
4) модуль нормального прискорення
;
4) модуль нормального прискорення
 .
.
Точка рухається по кривій з постійним тангенціальним прискоренням
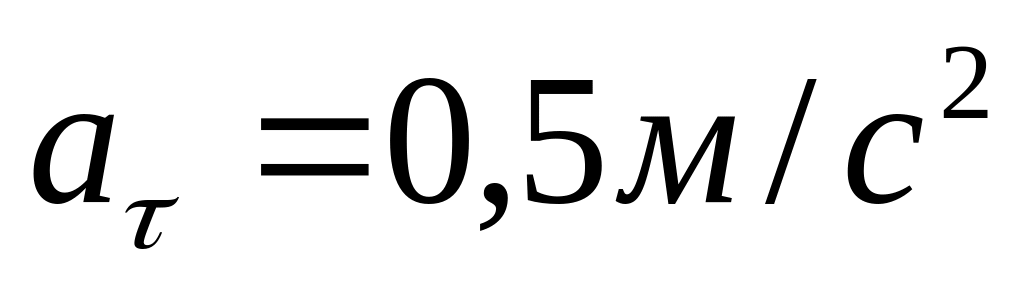 .
Визначити повне прискорення
точки на ділянці кривої з радіусом
кривизни
.
Визначити повне прискорення
точки на ділянці кривої з радіусом
кривизни
 ,
якщо точка рухається на цій ділянці зі
швидкістю
,
якщо точка рухається на цій ділянці зі
швидкістю
 .
.
За час
 точка пройшла шлях, рівний половині
довжини кола радіуса
точка пройшла шлях, рівний половині
довжини кола радіуса
 .
Визначити середню шляхову швидкість
за цей шлях і модуль вектора переміщення
середньої швидкості
.
Визначити середню шляхову швидкість
за цей шлях і модуль вектора переміщення
середньої швидкості
 .
.
Тіло, кинуте під деяким кутом до горизонту. Знайти цей кут, якщо горизонтальна дальність
 польоту тіла в чотири рази більша
максимальної висоти
польоту тіла в чотири рази більша
максимальної висоти
 траєкторії.
траєкторії.
Снаряд, випущений із знаряддя під кутом
 до горизонту, двічі був на одній і тій
же висоті
:
через час
до горизонту, двічі був на одній і тій
же висоті
:
через час
 і
і
 після пострілу. Визначити початкову
швидкість
після пострілу. Визначити початкову
швидкість
 і висоту
.
і висоту
.
Куля випущена з початковою швидкістю
 під кутом
під кутом
 до горизонту. Визначити максимальну
висоту
підйому, дальність
польоту і радіус
кривизни траєкторії кулі в її найвищій
точці. Опором повітря знехтувати.
до горизонту. Визначити максимальну
висоту
підйому, дальність
польоту і радіус
кривизни траєкторії кулі в її найвищій
точці. Опором повітря знехтувати.
Тіло кинуте під кутом
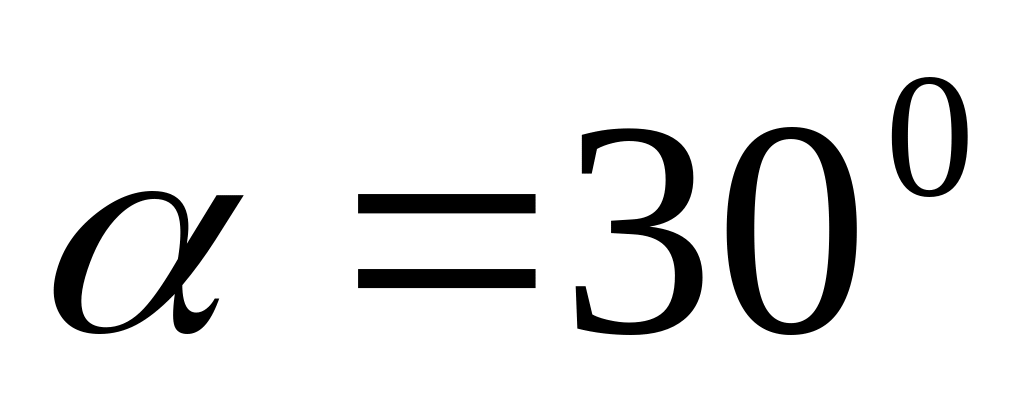 до горизонту. Знайти тангенціальне
до горизонту. Знайти тангенціальне
 і нормальне
і нормальне
 прискорення в початковий момент руху.
прискорення в початковий момент руху.
Першу половину свого шляху автомобіль рухався зі швидкістю
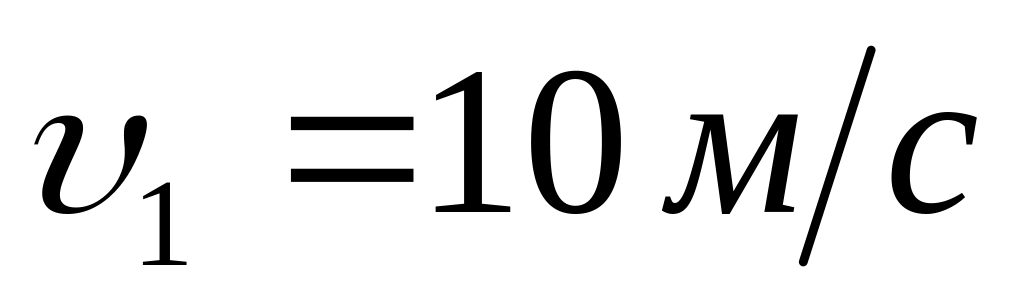 ,
а другу половину шляху – зі швидкістю
,
а другу половину шляху – зі швидкістю
 .
Яка середня швидкість руху автомобіля?
.
Яка середня швидкість руху автомобіля?
Тіло падає з висоти
 з нульовою початковою швидкістю.
Нехтуючи опором повітря, обчислити,
який шлях пройде тіло: 1) за першу секунду
свого падіння; 2) за останню секунду
свого падіння.
з нульовою початковою швидкістю.
Нехтуючи опором повітря, обчислити,
який шлях пройде тіло: 1) за першу секунду
свого падіння; 2) за останню секунду
свого падіння.
Тіло падає з висоти
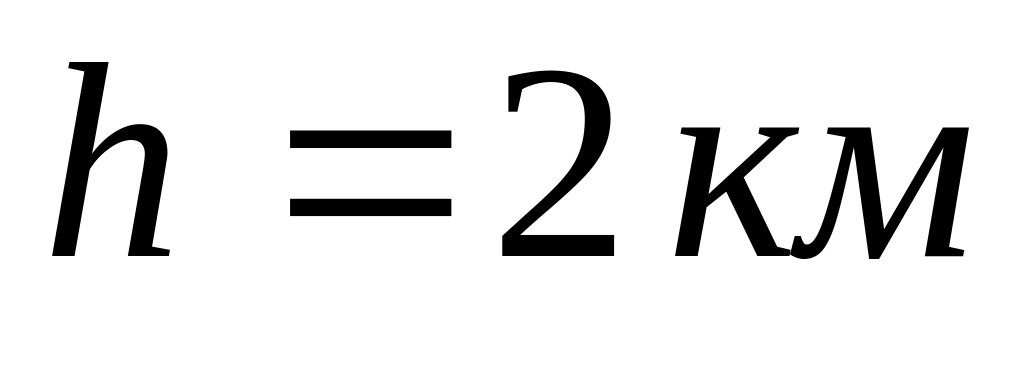 з початковою швидкістю, рівною нулю.
Нехтуючи опором повітря, знайти, який
час знадобиться тілу для проходження
перших
з початковою швидкістю, рівною нулю.
Нехтуючи опором повітря, знайти, який
час знадобиться тілу для проходження
перших
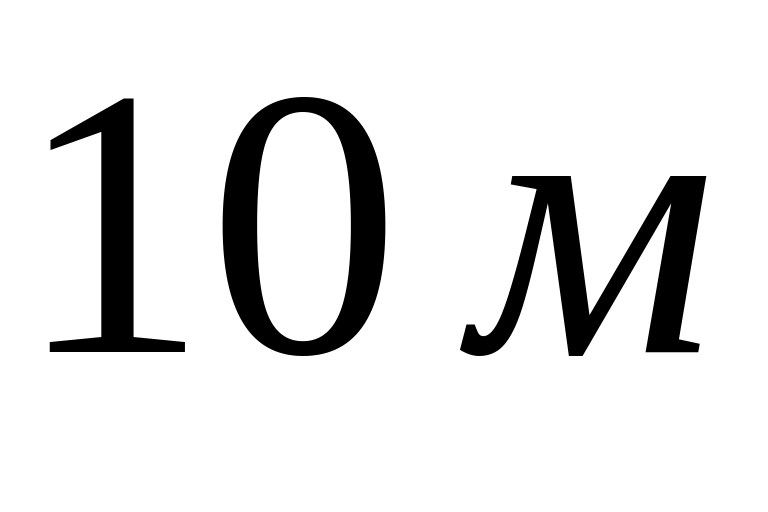 свого шляху.
свого шляху.
Тіло кинули зі швидкістю
 під кутом
під кутом
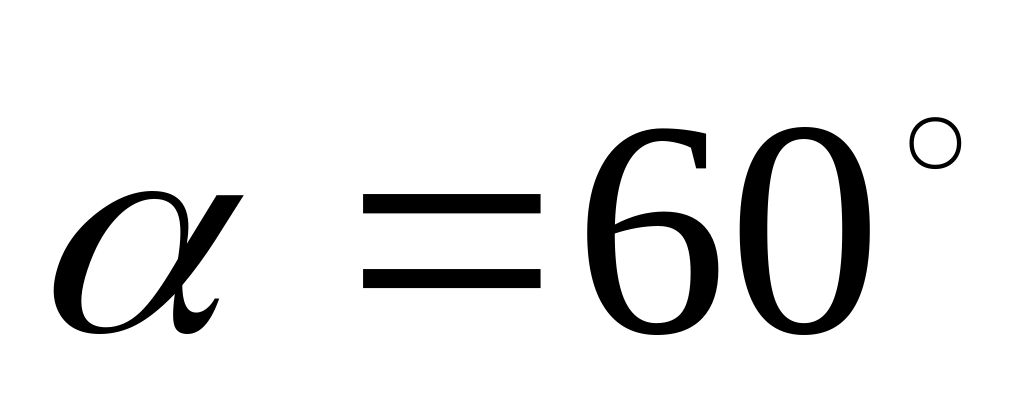 до горизонту. Нехтуючи опором повітря,
визначити швидкість тіла через
до горизонту. Нехтуючи опором повітря,
визначити швидкість тіла через
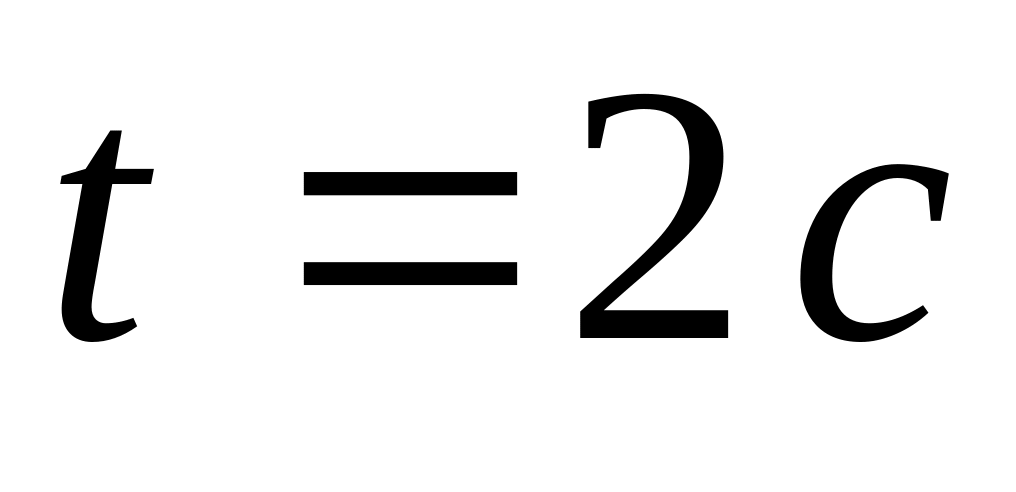 після
початку руху, а також модуль його
переміщення.
після
початку руху, а також модуль його
переміщення.
Тіло, що знаходиться на висоті
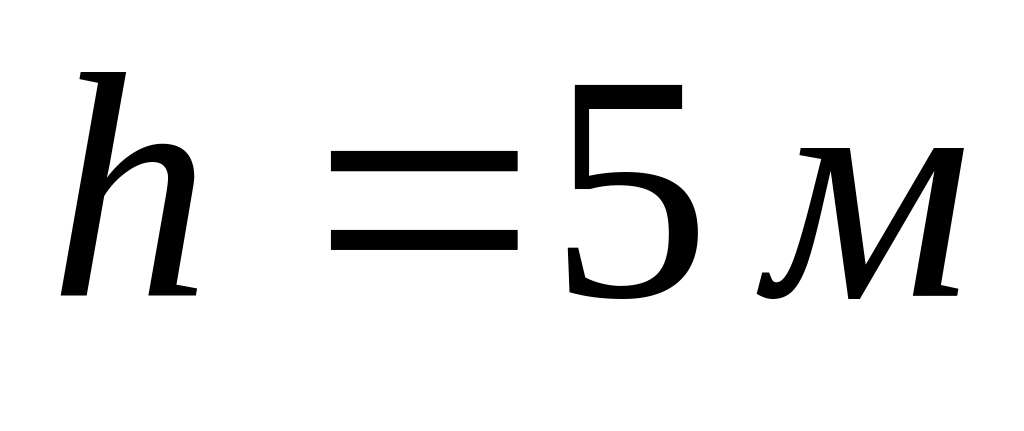 над поверхнею Землі,
кинули горизонтально зі швидкістю
над поверхнею Землі,
кинули горизонтально зі швидкістю
 .
Нехтуючи
опором повітря,
обчислити, з якою швидкістю тіло упаде
на землю.
.
Нехтуючи
опором повітря,
обчислити, з якою швидкістю тіло упаде
на землю.
Матеріальна точка рухається вздовж прямої так, що її прискорення лінійно збільшується і за перші
 досягає значення
досягає значення
 .
Знайти в кінці десятої секунди:
1) швидкість точки; 2) пройдений точкою
шлях.
.
Знайти в кінці десятої секунди:
1) швидкість точки; 2) пройдений точкою
шлях.
Із пункту А до пункту В, відстань між якими
 ,
одночасно назустріч один одному почали
рухатись два автомобілі: перший зі
швидкістю
,
одночасно назустріч один одному почали
рухатись два автомобілі: перший зі
швидкістю
 ,
другий –
,
другий –
 .
Визначити час, через який вони
зустрінуться, і відстань від пункту А
до місця зустрічі.
.
Визначити час, через який вони
зустрінуться, і відстань від пункту А
до місця зустрічі.
Лінійна швидкість точки, що знаходиться на ободі диска, який обертається, у три рази більша, ніж лінійна швидкість точки, що знаходиться на
 ближче до його осі. Знайти радіус диска.
ближче до його осі. Знайти радіус диска.
Колесо обертається з постійним кутовим прискоренням
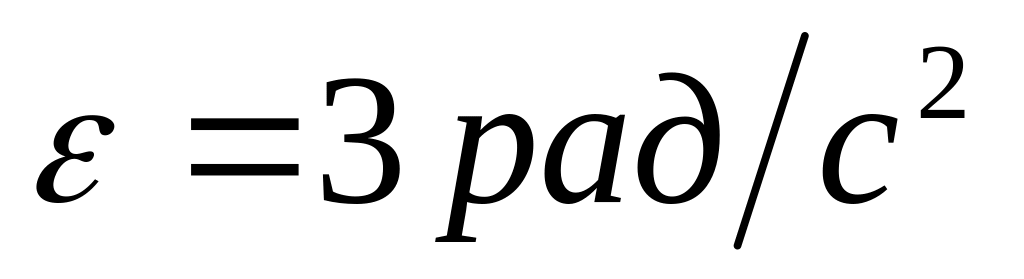 .
Знайти радіус колеса, якщо через
.
Знайти радіус колеса, якщо через
 після початку руху повне прискорення
колеса
після початку руху повне прискорення
колеса
 .
.
Колесо автомашини обертається рівносповільнено. За час
 воно змінило частоту обертання від
воно змінило частоту обертання від
 до
до
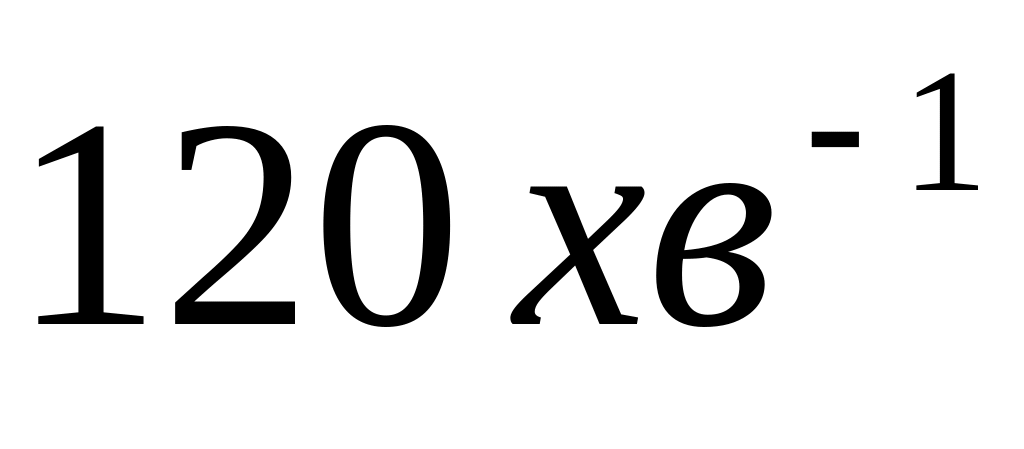 .
Знайти: 1) кутове прискорення колеса;
2) кількість повних обертів, що зробило
колесо за цей час.
.
Знайти: 1) кутове прискорення колеса;
2) кількість повних обертів, що зробило
колесо за цей час.
Точка рухається по колу радіусом
 з постійним тангенціальним прискоренням
з постійним тангенціальним прискоренням
 .
До кінця четвертого оберта після початку
руху лінійна швидкість точки
.
До кінця четвертого оберта після початку
руху лінійна швидкість точки
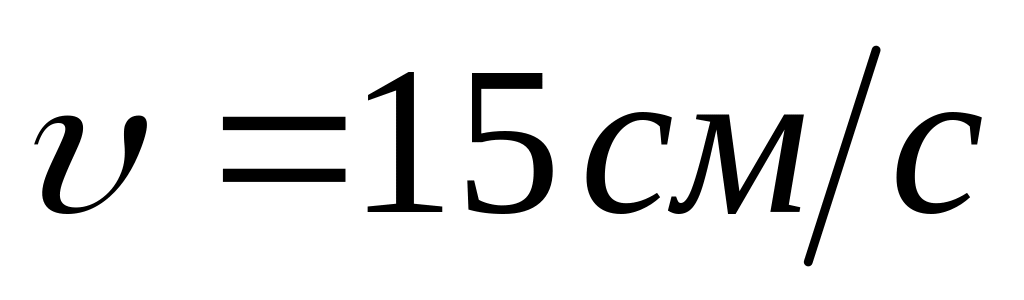 .
Знайти нормальне прискорення
точки через
.
Знайти нормальне прискорення
точки через
 після початку руху.
після початку руху.
Диск обертається навколо нерухомої вісі так, що залежність кута повороту радіуса диска від часу описується рівнянням
 .
Знайти
повне прискорення
.
Знайти
повне прискорення
 точки
на ободі диска до кінця другої секунди
після початку руху, якщо лінійна
швидкість точки в цей момент часу
точки
на ободі диска до кінця другої секунди
після початку руху, якщо лінійна
швидкість точки в цей момент часу
 .
.
Велосипедист рухається зі швидкістю
 .
Визначити доцентрове прискорення
велосипедиста та його кутову швидкість
на півколі довжиною
.
Визначити доцентрове прискорення
велосипедиста та його кутову швидкість
на півколі довжиною
 .
.
Тіло кинули з початковою швидкістю
 під кутом
під кутом
 до горизонту. Знайти
час польоту тіла та максимальну висоту
підняття. Опором
повітря знехтувати.
до горизонту. Знайти
час польоту тіла та максимальну висоту
підняття. Опором
повітря знехтувати.
Тіло обертається рівносповільнено з початковою частотою
 . Після
здійснення
. Після
здійснення
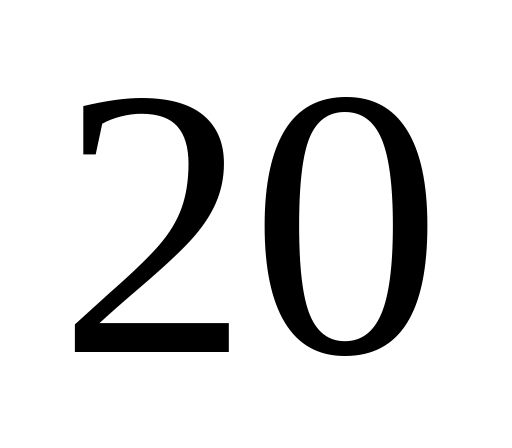 обертів,
частота його зменшилась до
обертів,
частота його зменшилась до
 . Знайти
кутове прискорення і час, протягом
якого змінилась частота обертання.
. Знайти
кутове прискорення і час, протягом
якого змінилась частота обертання.
Тіло обертається навколо нерухомої вісі за законом:
 .
Знайти
повне прискорення точки, що знаходиться
на відстані
.
Знайти
повне прискорення точки, що знаходиться
на відстані
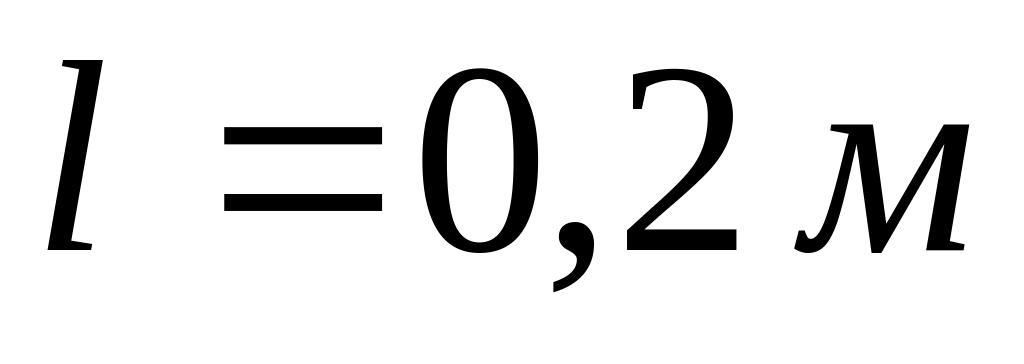 від вісі обертання для моменту часу
від вісі обертання для моменту часу
 .
.
Визначити траєкторію руху точки, заданої рівняннями:
 ;
;
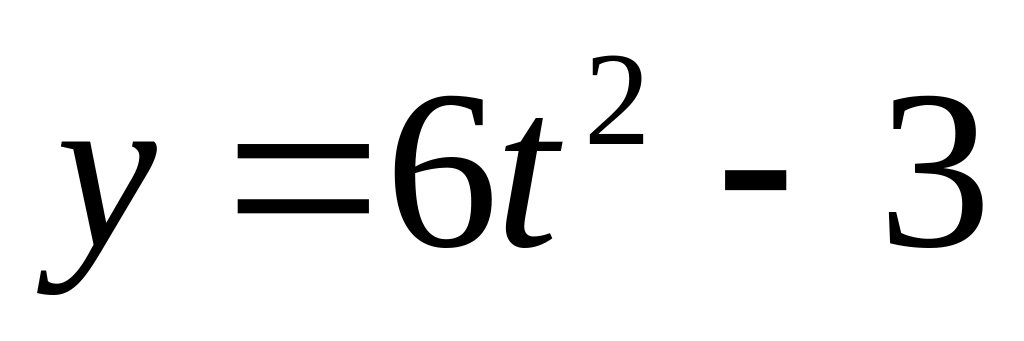 .
Побудувати графік залежності шляху,
пройденого точкою, від часу.
.
Побудувати графік залежності шляху,
пройденого точкою, від часу.
Людина стрибає у воду з крутого берега висотою з горизонтальною швидкістю
 .
Визначити модуль і напрямок швидкості
людини при досягненні нею води.
.
Визначити модуль і напрямок швидкості
людини при досягненні нею води.
Ескалатор піднімає людину, що стоїть на ньому, за час
 .
Якщо людина йде по нерухомому ескалатору,
то на піднімання витрачає
.
Якщо людина йде по нерухомому ескалатору,
то на піднімання витрачає
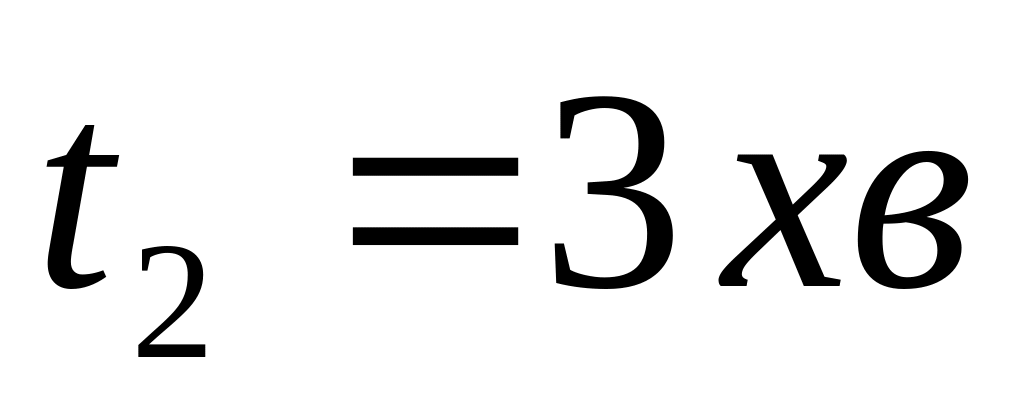 .
За який час людина підніметься, йдучи
по рухомому ескалатору?
.
За який час людина підніметься, йдучи
по рухомому ескалатору?
Залежність пройденого тілом шляху
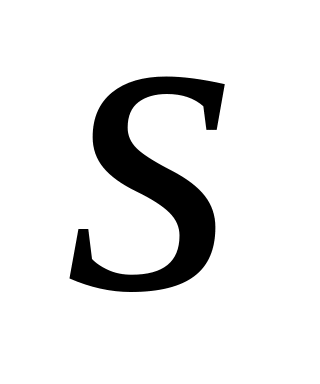 від часу
задається рівнянням
від часу
задається рівнянням
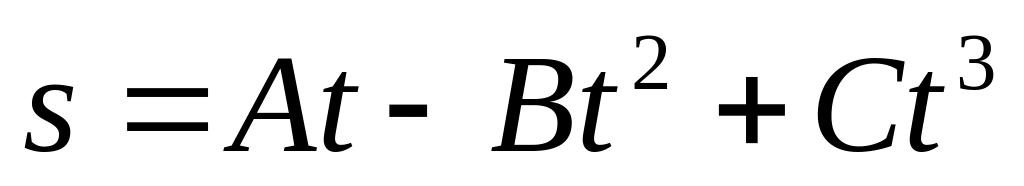 ,
де
,
де
 ,
,
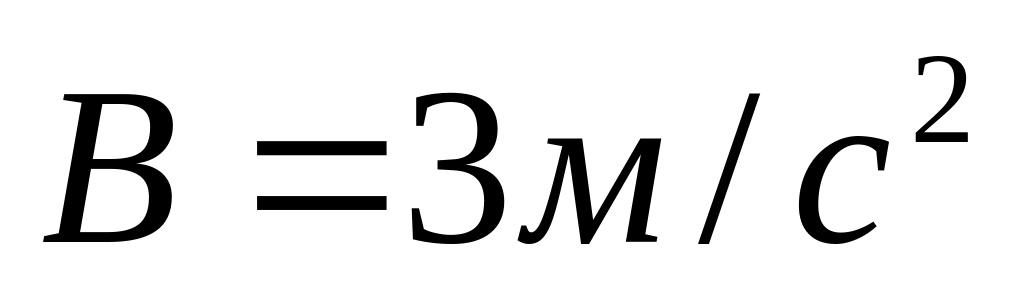 і
і
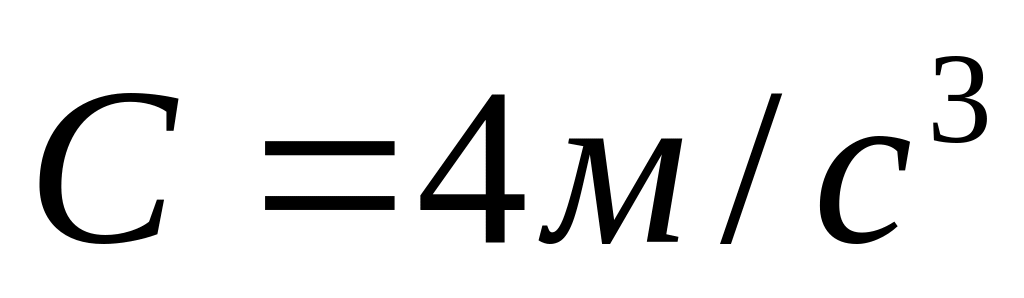 .
Знайти: 1) залежність швидкості
і прискорення
від часу
;
2) відстань, пройдену тілом, швидкість
та прискорення тіла через
.
Знайти: 1) залежність швидкості
і прискорення
від часу
;
2) відстань, пройдену тілом, швидкість
та прискорення тіла через
 після початку руху. Побудувати графік
шляху, швидкості і прискорення для
після початку руху. Побудувати графік
шляху, швидкості і прискорення для
 через
через
 .
.
Човен пливе по річці з одного пункту до іншого. У скільки разів час руху човна проти течії більший за час руху за течією, якщо швидкість течії
 ,
а швидкість човна відносно води
,
а швидкість човна відносно води

Від поштовху кулька закочується на похилу площину. На відстані
 від початку руху кулька була двічі:
через
від початку руху кулька була двічі:
через
 і
і
 після поштовху. Вважаючи рух
рівноприскореним, знайдіть початкову
швидкість
після поштовху. Вважаючи рух
рівноприскореним, знайдіть початкову
швидкість
 і прискорення
.
і прискорення
.
Два тягарці, маса яких
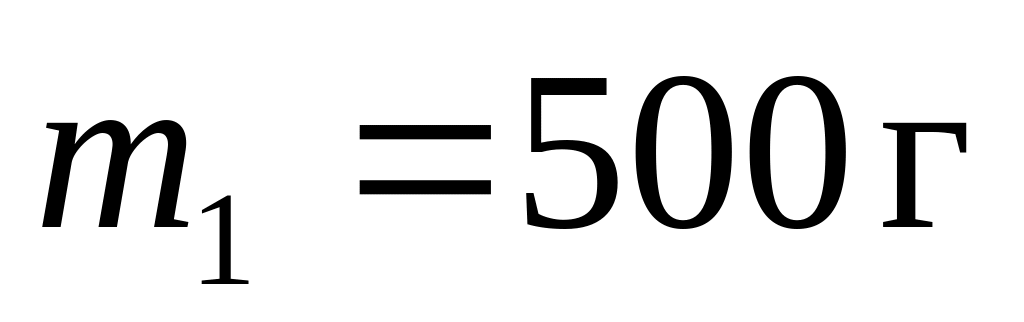 і
і
 ,
зв’язані невагомою ниткою та лежать
на гладкій горизонтальній
поверхні. До тягарця
прикладена горизонтально
направлена сила
,
зв’язані невагомою ниткою та лежать
на гладкій горизонтальній
поверхні. До тягарця
прикладена горизонтально
направлена сила
 .
Нехтуючи тертям, знайти:
1) прискорення тягарців; 2) силу натягу
нитки.
.
Нехтуючи тертям, знайти:
1) прискорення тягарців; 2) силу натягу
нитки.
 Найпростіша
машина Атвуда, яку застосовують для
вивчення законів рівноприскореного
руху, являє собою два тягарці з різними
масами
та
,
що підвішені на легкій нитці, перекинутій
через нерухомий блок (рис.
1). Вважаючи, що нитка та блок невагомі
та нехтуючи тертям на вісі блока, знайти:
1) прискорення
тягарців; 2) силу натягу нитки
.
Найпростіша
машина Атвуда, яку застосовують для
вивчення законів рівноприскореного
руху, являє собою два тягарці з різними
масами
та
,
що підвішені на легкій нитці, перекинутій
через нерухомий блок (рис.
1). Вважаючи, що нитка та блок невагомі
та нехтуючи тертям на вісі блока, знайти:
1) прискорення
тягарців; 2) силу натягу нитки
.
Тіло масою
 падає
вертикально з висоти
за час
.
Знайти силу опору при русі цього тіла.
падає
вертикально з висоти
за час
.
Знайти силу опору при русі цього тіла.
 В
установці (рис.
2) кут
нахилу площини до горизонту рівний
,
маси тіл
В
установці (рис.
2) кут
нахилу площини до горизонту рівний
,
маси тіл
 та
та
 ,
коефіцієнт тертя між другим тілом та
площиною
,
коефіцієнт тертя між другим тілом та
площиною
 .
Вважаючи,
що нитка і блок невагомі, знайти силу
натягу нитки
і прискорення, з яким будуть рухатись
ці тіла, якщо тіло
.
Вважаючи,
що нитка і блок невагомі, знайти силу
натягу нитки
і прискорення, з яким будуть рухатись
ці тіла, якщо тіло
 опускається.
опускається.
З колодязя висотою
 за допомогою мотузки рівноприскорено
піднімають відро з водою за
за допомогою мотузки рівноприскорено
піднімають відро з водою за
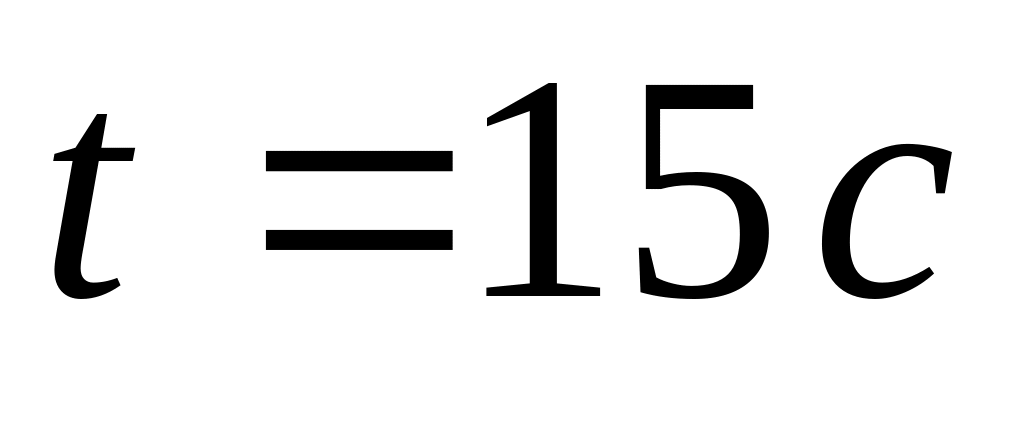 .
Маса відра з водою
.
Маса відра з водою
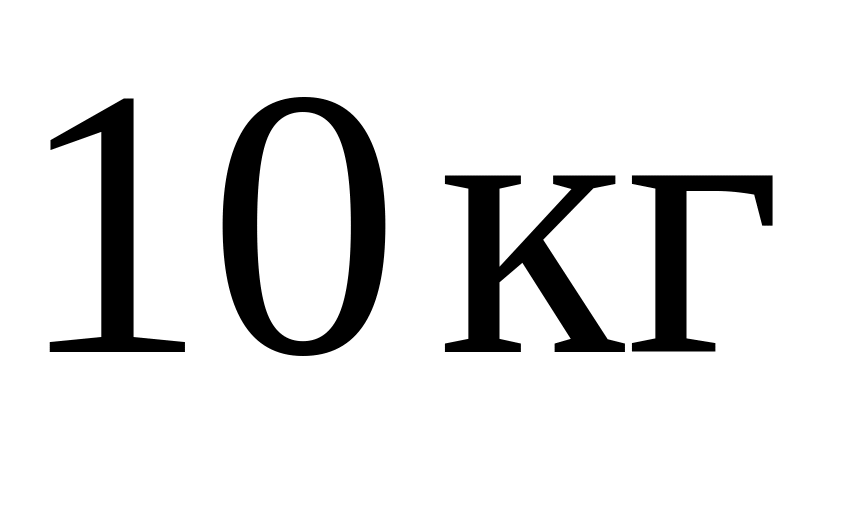 .
Визначити силу натягу мотузки.
.
Визначити силу натягу мотузки.
По похилій площині з кутом нахилу до горизонту
 ковзає тіло. Знайти швидкість тіла в
кінці другої секунди від початку
ковзання, якщо коефіцієнт
тертя
ковзає тіло. Знайти швидкість тіла в
кінці другої секунди від початку
ковзання, якщо коефіцієнт
тертя
 .
.
Д
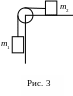 ва
тягарця однакової маси (
ва
тягарця однакової маси ( )
зв’язані ниткою та перекинуті через
невагомий блок, закріплений на кінці
столу
(рис. 3). Коефіцієнт
тертя тягарця
об стіл
.
Нехтуючи тертям в блоці, знайти:
1) прискорення, з яким рухаються тягарці;
2) силу натягу нитки.
)
зв’язані ниткою та перекинуті через
невагомий блок, закріплений на кінці
столу
(рис. 3). Коефіцієнт
тертя тягарця
об стіл
.
Нехтуючи тертям в блоці, знайти:
1) прискорення, з яким рухаються тягарці;
2) силу натягу нитки.
Автомобіль масою
 рушає з місця і перші
рушає з місця і перші
 проходить за
.
Знайти силу тяги двигуна автомобіля,
якщо коефіцієнт опору
проходить за
.
Знайти силу тяги двигуна автомобіля,
якщо коефіцієнт опору
 .
.
Кулька масою , прикріплена до нитки, описує коло в горизонтальній площині. Довжина нитки
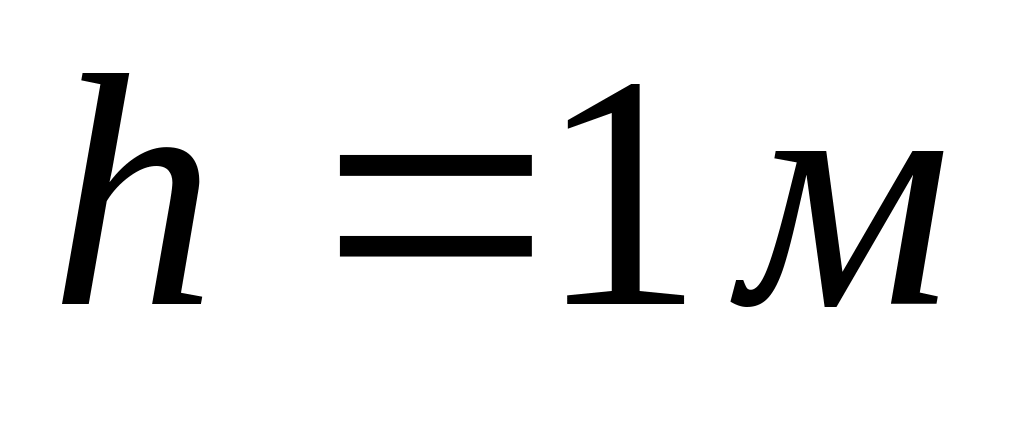 ,
кут між ниткою і вертикаллю
,
кут між ниткою і вертикаллю
 .
Знайти період обертання кульки.
.
Знайти період обертання кульки.
Кулька, що прикріплена до нитки, довжина якої
 ,
описує коло в горизонтальній площині.
Який кут
,
описує коло в горизонтальній площині.
Який кут
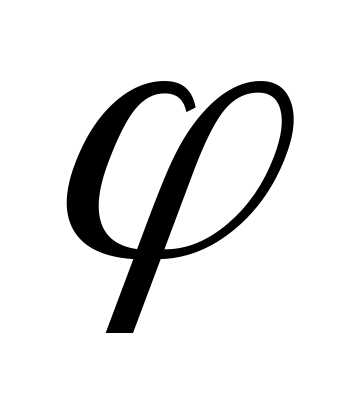 утворює нитка з вертикаллю, якщо частота
обертання
утворює нитка з вертикаллю, якщо частота
обертання
 ?
?
Автомобіль масою
 рухається з постійною швидкістю
рухається з постійною швидкістю
 .
З якою силою автомобіль тисне на
середину: 1) горизонтального містка; 2)
опуклого; 3) вгнутого містка, радіус
кривизни яких
.
З якою силою автомобіль тисне на
середину: 1) горизонтального містка; 2)
опуклого; 3) вгнутого містка, радіус
кривизни яких
 ?
?
Якої ваги баласт треба скинути з аеростата який рівномірно опускається, щоб він почав рівномірно підніматися з тією ж швидкістю? Вага аеростата з баластом
 ,
підйомна сила аеростата
,
підйомна сила аеростата
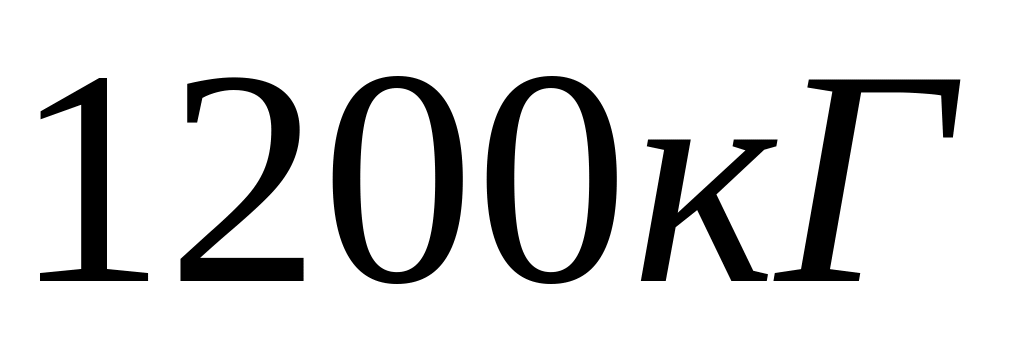 .
Силу опору повітря вважати однаковою
при підйомі та при спуску.
.
Силу опору повітря вважати однаковою
при підйомі та при спуску.
Сталевий дріт деякого діаметра витримує вантаж до
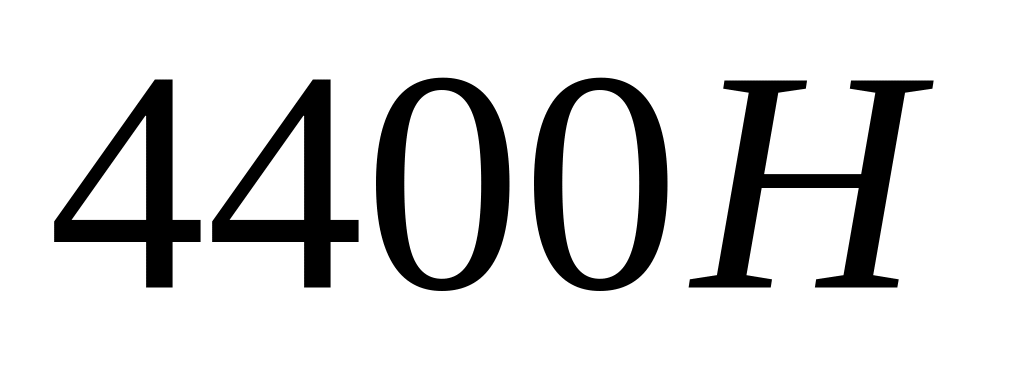 .
З яким найбільшим прискоренням можна
піднімати вантаж у
.
З яким найбільшим прискоренням можна
піднімати вантаж у
 ,
підвішений на дроті, щоб він при цьому
не розірвався?
,
підвішений на дроті, щоб він при цьому
не розірвався?
Вага ліфта з пасажирами рівна
 .
Знайти, з яким прискоренням і в якому
напрямку рухається ліфт, якщо відомо,
що натяг троса, який підтримує ліфт,
рівний: 1)
;
2)
.
Знайти, з яким прискоренням і в якому
напрямку рухається ліфт, якщо відомо,
що натяг троса, який підтримує ліфт,
рівний: 1)
;
2)
 .
.
Яку силу треба прикласти до вагону, який стоїть на рейках, щоб вагон став рухатися рівноприскорено і за час
 пройшов шлях
пройшов шлях
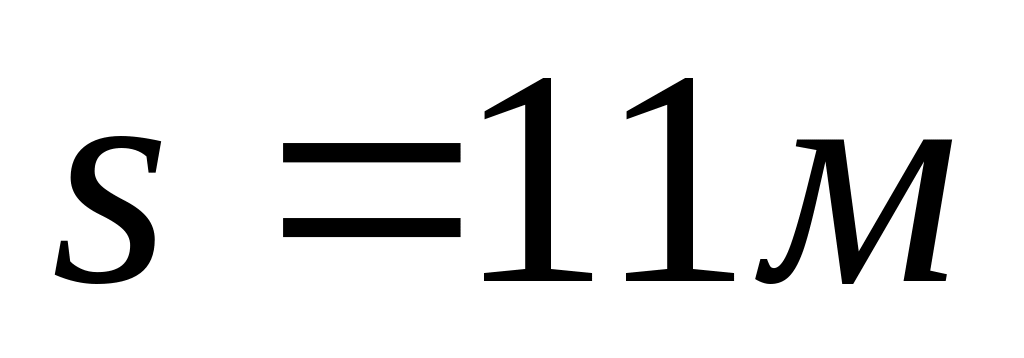 ?
Вага вагону
?
Вага вагону
 .
За час руху на вагон діє сила тертя,
рівна
.
За час руху на вагон діє сила тертя,
рівна
 ваги вагона.
ваги вагона.
Тіло масою
 рухається прямолінійно, при чому
залежність пройденого тілом шляху
від часу
задається рівнянням
рухається прямолінійно, при чому
залежність пройденого тілом шляху
від часу
задається рівнянням
 ,
де
,
де
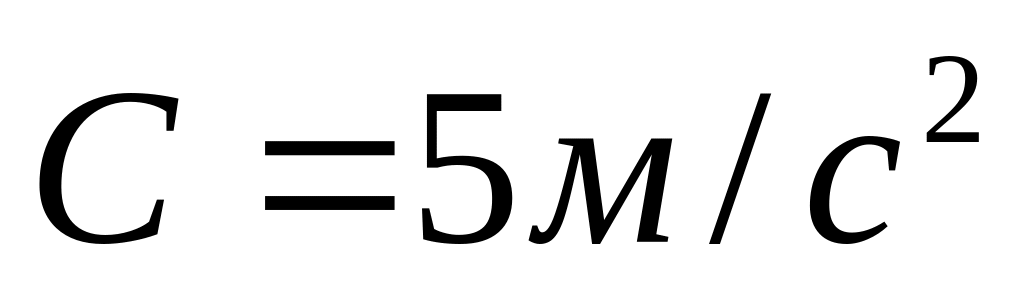 і
і
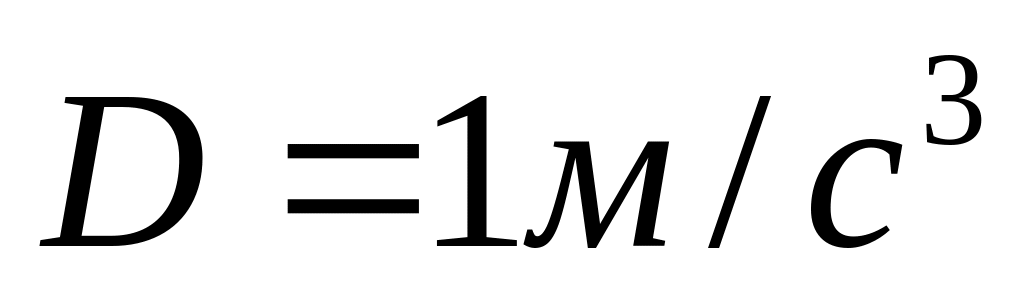 .
Знайти величину сили, яка діє на тіло
в кінці першої секунди руху.
.
Знайти величину сили, яка діє на тіло
в кінці першої секунди руху.
Молекула масою
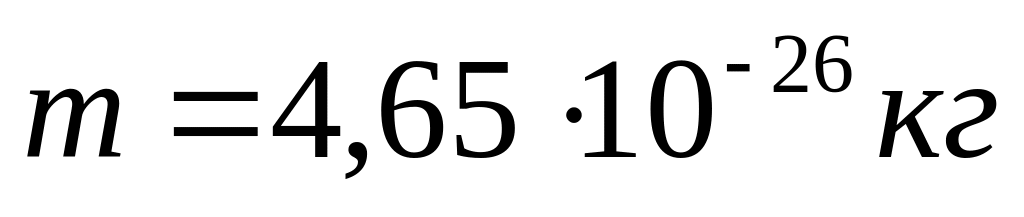 ,
яка
летить по нормалі до стінки посудини
зі швидкістю
,
яка
летить по нормалі до стінки посудини
зі швидкістю
 ,
ударяється об стінку і пружно відскакує
від неї без втрати швидкості. Знайти
імпульс сили, отриманої стінкою за час
удару.
,
ударяється об стінку і пружно відскакує
від неї без втрати швидкості. Знайти
імпульс сили, отриманої стінкою за час
удару.
Молекула масою
 ,
яка
летить зі швидкістю
,
ударяться об стінку посудини під кутом
,
яка
летить зі швидкістю
,
ударяться об стінку посудини під кутом
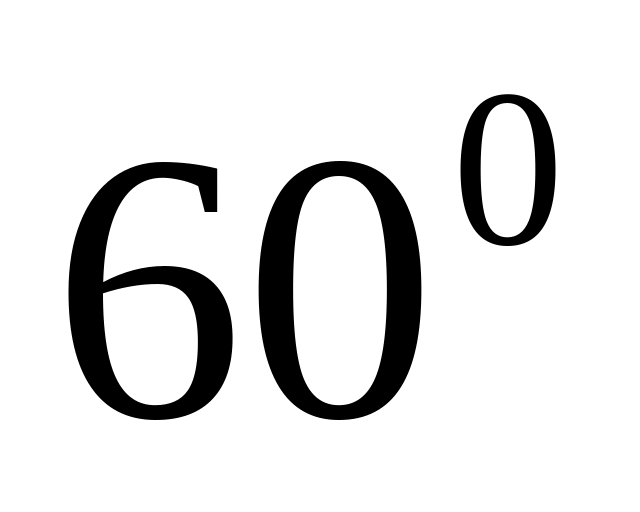 до нормалі і під таким же кутом пружно
відскакує від неї без втрати швидкості.
Знайти імпульс сили, отриманої стінкою
за час удару.
до нормалі і під таким же кутом пружно
відскакує від неї без втрати швидкості.
Знайти імпульс сили, отриманої стінкою
за час удару.
Який кут з горизонтом складає поверхня бензину в баку автомобіля, який рухається горизонтально з постійним прискоренням

 ?
?
До стелі трамвайного вагону підвішена на нитці куля. Вагон гальмує і його швидкість рівномірно змінюється за час
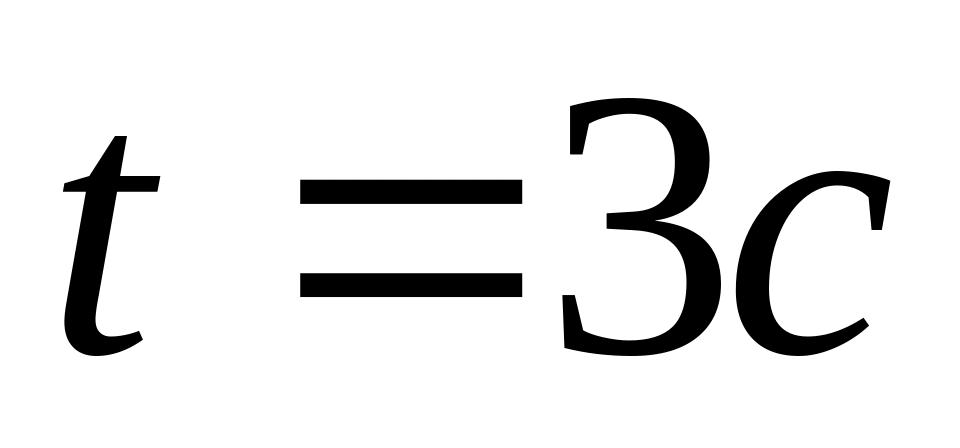 від
від
 до
до
 .
На який кут
відхилиться при цьому нитка з кулею?
.
На який кут
відхилиться при цьому нитка з кулею?
Під дією постійної сили
 тіло рухається прямолінійно так, що
залежність пройденої тілом відстані
від часу
задається рівнянням
тіло рухається прямолінійно так, що
залежність пройденої тілом відстані
від часу
задається рівнянням
 .
Знайти масу тіла, якщо стала
.
Знайти масу тіла, якщо стала
 .
.
Мотоцикліст їде по горизонтальній дорозі зі швидкістю
 ,
виконуючи поворот радіусом кривизни
в
,
виконуючи поворот радіусом кривизни
в
 .
Наскільки при цьому він повинен
нахилитися, щоб не впасти при повороті?
.
Наскільки при цьому він повинен
нахилитися, щоб не впасти при повороті?
Камінь, прив’язаний до мотузки, рівномірно обертається у вертикальній площині. Знайти масу каменя, якщо відомо, що різниця між максимальним і мінімальним натягом мотузки рівна

Відро з водою прив’язане до мотузки довжиною
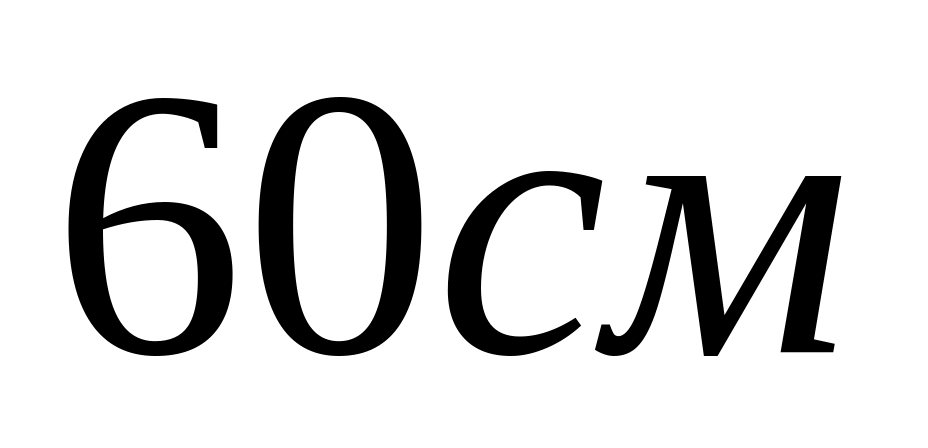 ,
рівномірно обертається у вертикальній
площині. Знайти: 1) найменшу швидкість
обертання відра, при якій у найвищій
точці вода з нього не виливається, 2)
натяг мотузки у найвищій і найнижчих
точках кола. Маса відра з водою
,
рівномірно обертається у вертикальній
площині. Знайти: 1) найменшу швидкість
обертання відра, при якій у найвищій
точці вода з нього не виливається, 2)
натяг мотузки у найвищій і найнижчих
точках кола. Маса відра з водою
 .
.
Під дією деякої сили тіло масою
 здійснює прямолінійний рух, який
описується рівнянням
здійснює прямолінійний рух, який
описується рівнянням
 .
Чому рівна діюча на тіло сила в момент
часу
.
Чому рівна діюча на тіло сила в момент
часу
 ?
Побудуйте графік залежності сили від
часу.
?
Побудуйте графік залежності сили від
часу.
Яка швидкість кулі при вильоті із духової рушниці, якщо її маса
 ,
довжина ствола
,
довжина ствола
 ,
калібр
,
калібр
 ,
а середній тиск повітря під час пострілу
,
а середній тиск повітря під час пострілу
 ?
?
Автомобіль з вимкненим двигуном рухається вгору по похилій дорозі зі швидкістю
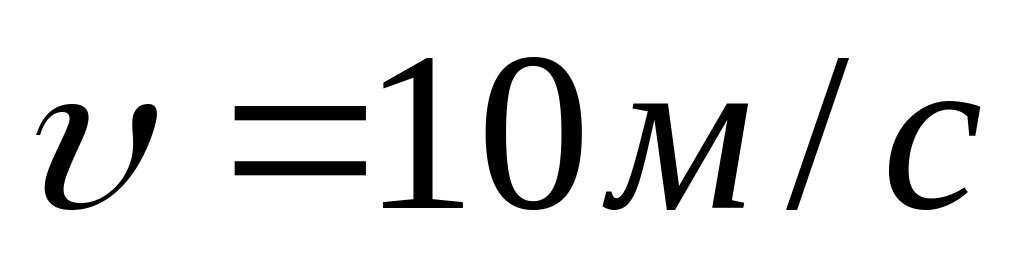 .
Визначити шлях, пройдений автомобілем
до зупинки, і час його руху, якщо
коефіцієнт тертя
.
Визначити шлях, пройдений автомобілем
до зупинки, і час його руху, якщо
коефіцієнт тертя
 ,
а кут нахилу
,
а кут нахилу
 .
.
На горизонтальній поверхні лежить тіло масою
 .
Який шлях пройде це тіло за
.
Який шлях пройде це тіло за
 ,
якщо до нього прикласти силу
,
якщо до нього прикласти силу
 ,
яка утворює кут
,
яка утворює кут
 з горизонтом? Коефіцієнт тертя між
тілом і поверхнею
з горизонтом? Коефіцієнт тертя між
тілом і поверхнею
 .
.
До динамометра, який підвішений в кабінці ліфта, прикріплений вантаж масою . Ліфт рухається вгору. Визначте прискорення ліфта, вважаючи його однаковим по модулю при розгоні і гальмуванні, якщо відомо, що під час розгону покази динамометра більші, чим при гальмуванні, на
 .
.
Через нерухомий блок перекинута нитка, на одному кінці якої підвішений вантаж масою
 ,
а на другому кінці другий блок
,
а на другому кінці другий блок
 .
Через блок
також перекинута нитка, на кінцях якої
підвішені вантажі масами
.
Через блок
також перекинута нитка, на кінцях якої
підвішені вантажі масами
 і
і
 .
З яким прискоренням буде рухатися блок
,
якщо всю систему надати самій собі?
Масу блоків і ниток не враховувати.
Дослідити можливі випадки.
.
З яким прискоренням буде рухатися блок
,
якщо всю систему надати самій собі?
Масу блоків і ниток не враховувати.
Дослідити можливі випадки.
На візку, що рухається в горизонтальному напрямку з прискоренням
 ,
встановлений схил. Знайти натяг нитки
схилу і кут, який утворює нитка з
вертикаллю, якщо маса підвішеного на
нитці вантажу
,
встановлений схил. Знайти натяг нитки
схилу і кут, який утворює нитка з
вертикаллю, якщо маса підвішеного на
нитці вантажу
 .
.
Ракета з рідким паливом масою
 запускається у вертикальному напрямку.
Витрата палива
запускається у вертикальному напрямку.
Витрата палива
 .
На яку висоту підніметься ракета за
час роботи двигуна
.
На яку висоту підніметься ракета за
час роботи двигуна
 ,
якщо швидкість витікання газів із сопла
,
якщо швидкість витікання газів із сопла
 ?
?
При якій швидкості автомобіля тиск, що створюється ним на увігнутий міст, у
 рази більший тиску на випуклий міст?
Радіус кривизни мостів в обох випадках
рази більший тиску на випуклий міст?
Радіус кривизни мостів в обох випадках
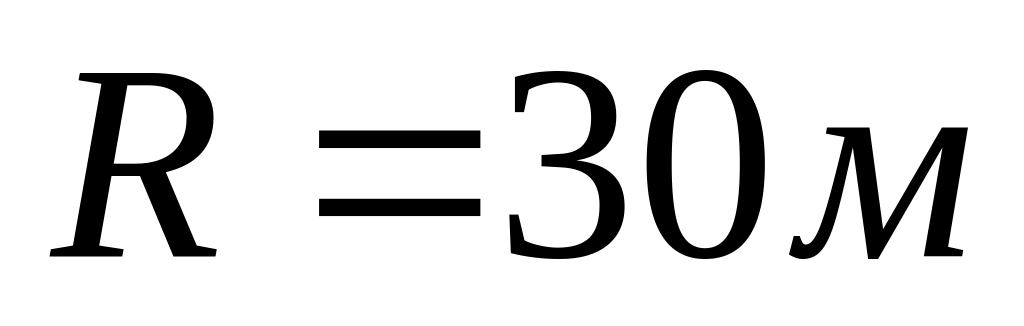 .
.
Всередині вертикально розміщеного конусу з кутом при вершині
 знаходиться тіло. На якій мінімальній
відстані від вершини конуса може
знаходитися тіло, якщо коефіцієнт тертя
між тілом і поверхнею конуса
знаходиться тіло. На якій мінімальній
відстані від вершини конуса може
знаходитися тіло, якщо коефіцієнт тертя
між тілом і поверхнею конуса
 ,
а конус обертається навколо своєї осі
з кутовою швидкістю
,
а конус обертається навколо своєї осі
з кутовою швидкістю
 ? Чому рівне максимальне значення цієї
відстані?
? Чому рівне максимальне значення цієї
відстані?
Тіло розміщено на похилій площині з кутом нахилу . Коефіцієнт тертя становить
 .
У скільки разів мінімальна сила
.
У скільки разів мінімальна сила
 ,
з якою треба подіяти на тіло, щоб
витягнути його на похилу площину, більша
за силу
,
з якою треба подіяти на тіло, щоб
витягнути його на похилу площину, більша
за силу
 ,
потрібну для утримання тіла на похилій
площині?
,
потрібну для утримання тіла на похилій
площині?
Літак виконує «мертву петлю» радіуса
 .
Визначити вагу льотчика
.
Визначити вагу льотчика
 ,
маса якого
,
маса якого
 ,
у момент, коли швидкість літака
,
у момент, коли швидкість літака
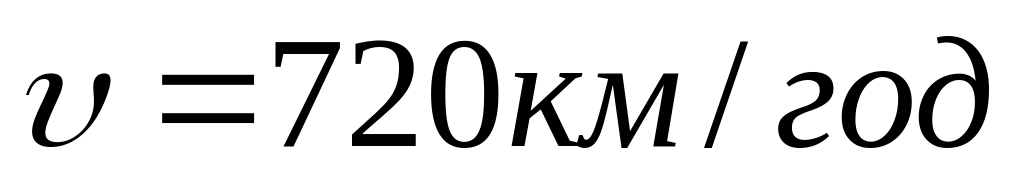 ,
а вектор швидкості
утворює
кут
,
а вектор швидкості
утворює
кут
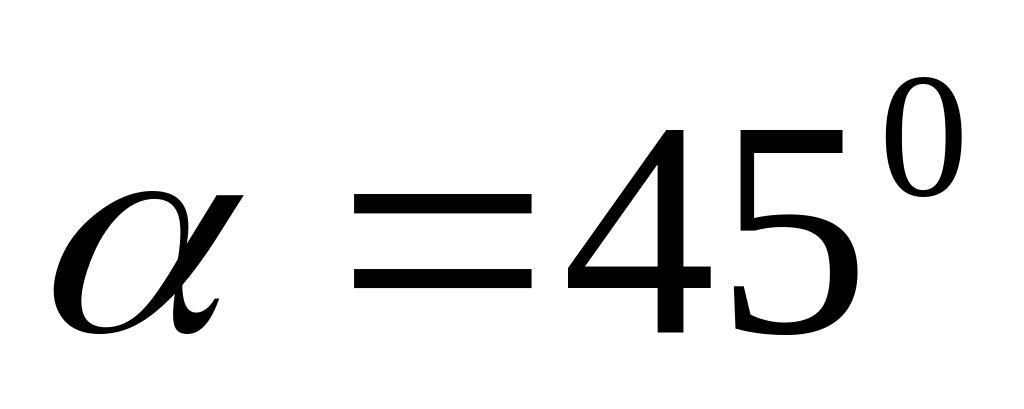 з горизонталлю.
з горизонталлю.
Визначити силу , що діє на частинку масою , координати якої змінюються згідно з рівняннями
 ,
,
 ,
де
,
де
 – сталі.
– сталі.
Тіло, маса якого
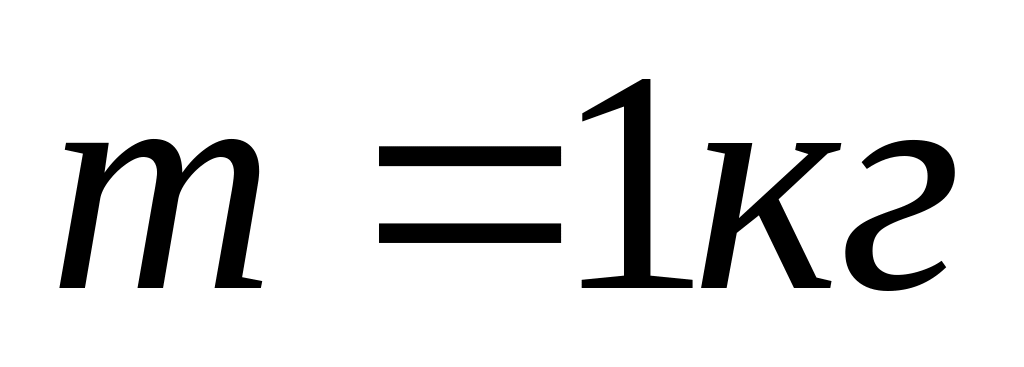 ,
обертається на нитці у вертикальній
площині. На скільки сила натягу
,
обертається на нитці у вертикальній
площині. На скільки сила натягу
 нитки в нижній точці буде більшою, ніж
у верхній
нитки в нижній точці буде більшою, ніж
у верхній
 ?
?
Велосипедист рухається зі швидкістю по заокругленню дороги радіуса
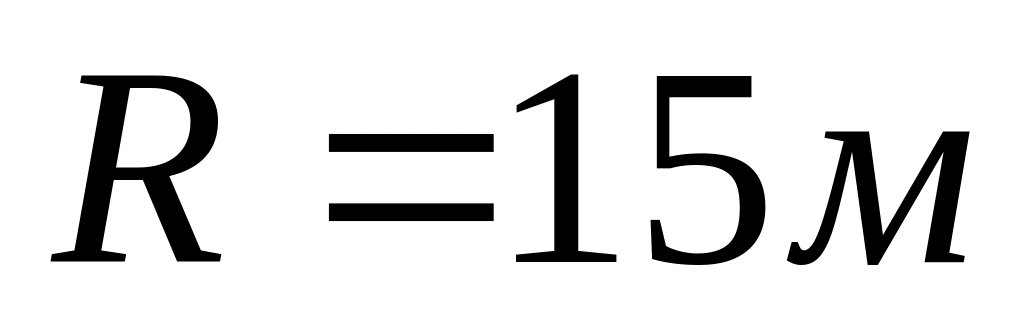 .
Обчислити кут
нахилу площини велосипеда до вертикалі,
а також найменший коефіцієнт тертя
між шинами велосипеда і дорогою, за
яких забезпечується стійкість
велосипедиста.
.
Обчислити кут
нахилу площини велосипеда до вертикалі,
а також найменший коефіцієнт тертя
між шинами велосипеда і дорогою, за
яких забезпечується стійкість
велосипедиста.
У скільки разів потрібно було б збільшити швидкість обертання Землі навколо своєї вісі, щоб тіла на екваторі важили вдвічі менше, ніж на полюсі? Вважайте, що форма Землі не змінилася б.
Обчислити у скільки разів сила тяжіння на Землі більша сили тяжіння на Марсі, якщо радіус Марса становить
 радіуса Землі, а маса Марса –
радіуса Землі, а маса Марса –
 маси Землі.
маси Землі.
Обчислити середню швидкість руху Місяця по орбіті, вважаючи середню відстань його до Землі
 ,
а масу Землі
,
а масу Землі
 .
.
Обчислити висоту, на якій прискорення вільного падіння складає
 від прискорення вільного падіння на
поверхні Землі.
від прискорення вільного падіння на
поверхні Землі.
З якою швидкістю рухається Земля навколо Сонця? Вважати, що Земля рухається по коловій орбіті.
Оцініть масу Сонця, вважаючи відстань від Землі до Сонця рівною
 .
.
Супутник рухається по коловій орбіті на висоті від поверхні Землі. Запишіть швидкість супутника і період його обертання через , радіус Землі і прискорення сили тяжіння на поверхні Землі .
Штучний супутник Землі рухається навколо неї по коловій орбіті на висоті
 .
Обчислити швидкість його руху.
.
Обчислити швидкість його руху.
Обчислити період обертання штучного супутника навколо Землі, який рухається по коловій орбіті на висоті, що дорівнює її радіусу.
Місяць робить один повний оберт навколо Землі за час
 . Знайти
масу Землі.
. Знайти
масу Землі.
Початкова швидкість кулі, маса якої
 ,
дорівнює
,
дорівнює
 .
При горизонтальному русі в повітрі за
час
.
При горизонтальному русі в повітрі за
час
 її швидкість зменшилася до значення
її швидкість зменшилася до значення
 .
Визначити коефіцієнт опору
,
вважаючи, що сила опору пропорційна
квадратові швидкості кулі.
.
Визначити коефіцієнт опору
,
вважаючи, що сила опору пропорційна
квадратові швидкості кулі.
Залізничний вагон гальмується і його швидкість рівномірно змінюється за час
 від
від
 до
до
 .
При якому граничному значенні коефіцієнт
тертя між валізою і полицею, валіза при
гальмуванні починає ковзати на поличці?
.
При якому граничному значенні коефіцієнт
тертя між валізою і полицею, валіза при
гальмуванні починає ковзати на поличці?
Тіло ковзає по похилій площині, яка складає з горизонтом кут . Пройшовши відстань
 ,
тіло набуває швидкості
.
Чому рівний коефіцієнт тертя тіла об
площину?
,
тіло набуває швидкості
.
Чому рівний коефіцієнт тертя тіла об
площину?
Канат лежить на столі так, що частина його звисає зі столу, і починає ковзати тоді, коли довжина звисаючої частини складає
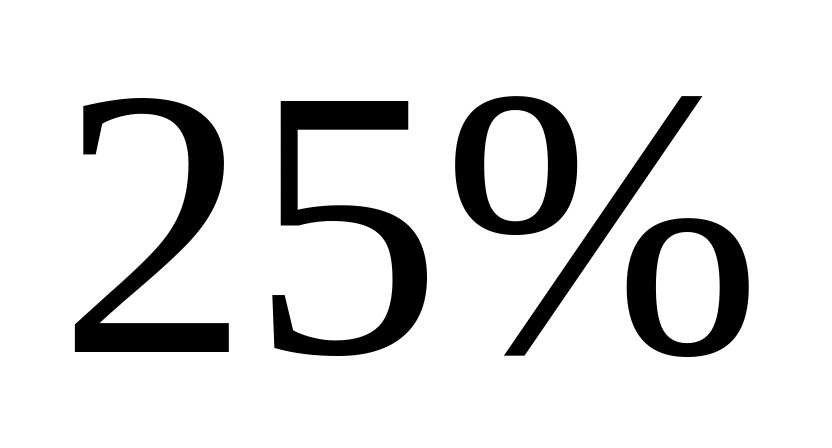 всієї його довжини. Чому рівний коефіцієнт
тертя канату об стіл?
всієї його довжини. Чому рівний коефіцієнт
тертя канату об стіл?
Тіло лежить на похилій площині, яка складає з горизонтом кут
 .1)при
якому граничному значенні коефіцієнта
тертя тіло почне зсковзувати з похилої
площини 2) з яким прискоренням буде
зсковзувати тіло з площини, якщо
коефіцієнт тертя рівний
.1)при
якому граничному значенні коефіцієнта
тертя тіло почне зсковзувати з похилої
площини 2) з яким прискоренням буде
зсковзувати тіло з площини, якщо
коефіцієнт тертя рівний
 ?
3) скільки часу потрібно для проходженнях
при цих умовах
шляху? 4) яку швидкість тіло буде мати
в кінці цих
?
?
3) скільки часу потрібно для проходженнях
при цих умовах
шляху? 4) яку швидкість тіло буде мати
в кінці цих
?
Вантаж вагою
 ,
прив’язаний до гумового шнура довжиною
,
прив’язаний до гумового шнура довжиною
 ,
відхиляють на кут
,
відхиляють на кут
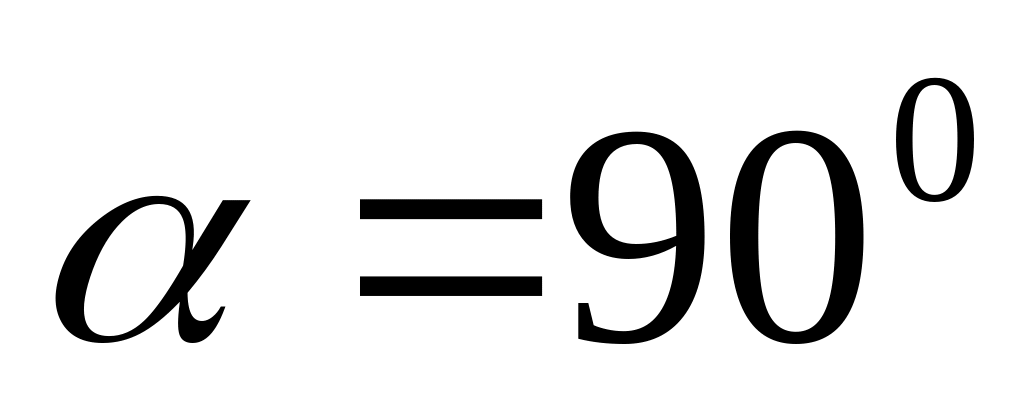 і відпускають. Знайти довжину
гумового шнура в момент проходження
положення рівноваги. Коефіцієнт
деформації гумового шнура рівний
і відпускають. Знайти довжину
гумового шнура в момент проходження
положення рівноваги. Коефіцієнт
деформації гумового шнура рівний
 .
.
Яке навантаження потрібно прикласти до алюмінієвого стержня, щоб він при температурі
 мав ту ж саму довжину, що і при
мав ту ж саму довжину, що і при
 ? Площа поперечного перерізу стержня
? Площа поперечного перерізу стержня
 .
Модуль Юнга
.
Модуль Юнга
 .
.
Гумовий шнур розтягнутий так, що його довжина збільшилась у два рази. Який діаметр розтягнутого шнура, якщо до деформації він був рівний
 ,
а коефіцієнт Пуассона для гуми
,
а коефіцієнт Пуассона для гуми
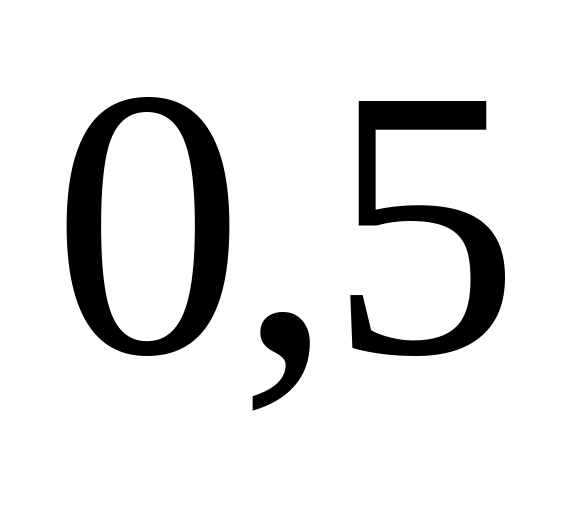 ?
?
При якій довжині підвішений вертикально сталевий дріт починає розриватися під дією власної ваги? Границя міцності сталі
 .
.
Визначити відносне видовження мідного стержня, якщо при його розтягненні здійснюється робота
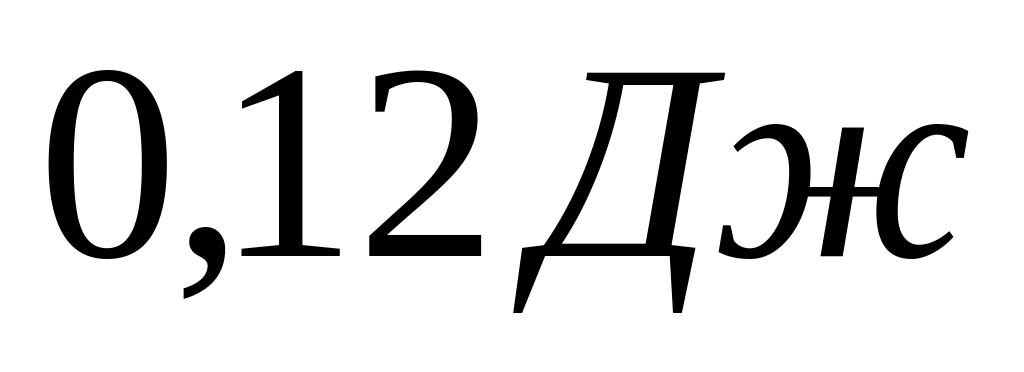 .
Довжина стержня
.
Довжина стержня
 ,
площа його поперечного перерізу
,
площа його поперечного перерізу
 .
.
Визначити силу, з якою гімнаст масою
 діє на пружну сітку при стрибку з висоти
діє на пружну сітку при стрибку з висоти
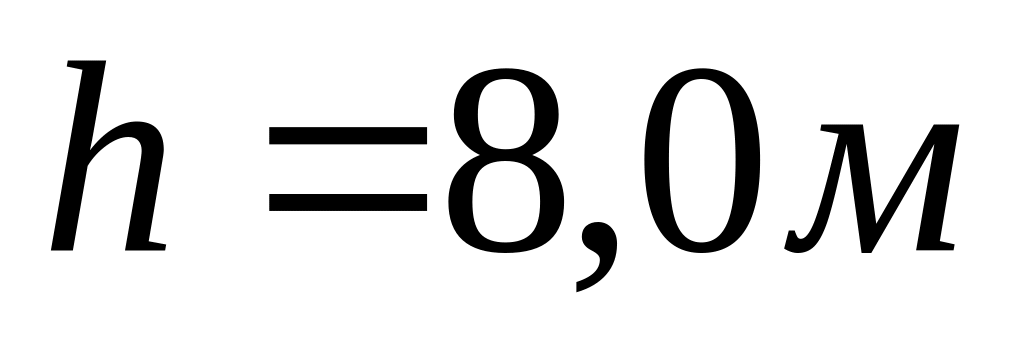 ,
якщо під дією сили тяжіння гімнаста
сітка прогинається на
,
якщо під дією сили тяжіння гімнаста
сітка прогинається на
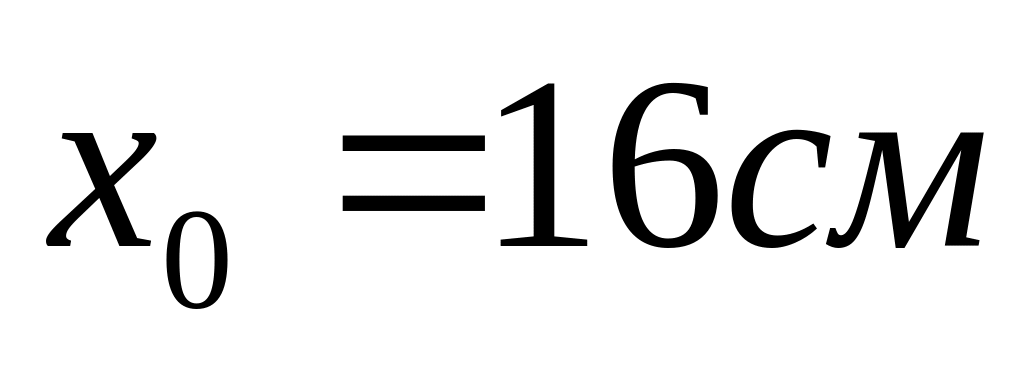 .
.
Яку силу необхідно прикласти для натягу луку на
 ,
якщо вся виконана робота іде на надання
стрілі кінетичної енергії? Найбільша
дальність польоту стріли
,
якщо вся виконана робота іде на надання
стрілі кінетичної енергії? Найбільша
дальність польоту стріли
 ,
маса стріли
,
маса стріли
 .
.
Знайти другу космічну швидкість, тобто найменше значення швидкості при якій ракета може віддалитися від Землі, вийшовши за межі поля тяжіння.
Перший штучний супутник Землі мав період обертання

 .
Вважаючи орбіту супутника колом, а рух
рівномірним, визначити висоту польоту
супутника над поверхнею Землі.
.
Вважаючи орбіту супутника колом, а рух
рівномірним, визначити висоту польоту
супутника над поверхнею Землі.
Яку швидкість необхідно надати тілу, щоб воно могло віддалитися з поверхні Місяця в нескінечність? Маса Місяця
 ,
радіус Місяця
,
радіус Місяця
 .
.
З якою швидкістю рухається навколо Сонця Земля, якщо відстань між ними близько
 ,
а маса Сонця
,
а маса Сонця
 ?
?
Визначити напруженість
 гравітаційного поля на висоті
гравітаційного поля на висоті
 над поверхнею Землі. Вважати відомим
прискорення
вільного падіння біля поверхні Землі
і її радіус
.
над поверхнею Землі. Вважати відомим
прискорення
вільного падіння біля поверхні Землі
і її радіус
.
На якій відстані від центра Землі знаходиться точка, в якій напруженість сумарного гравітаційного поля Землі і Місяця рівна нулю? Прийняти, що маса Землі у
 раз більша за масу Місяця і що відстань
від центру Землі до центру Місяця рівна
раз більша за масу Місяця і що відстань
від центру Землі до центру Місяця рівна
 радіусам Землі.
радіусам Землі.
Визначити лінійну і кутову швидкості супутника Землі, який обертається по коловій орбіті на висоті
 .
Прискорення вільного падіння
біля поверхні Землі і її радіус
вважати відомими.
.
Прискорення вільного падіння
біля поверхні Землі і її радіус
вважати відомими.
З якою силою взаємодіє частинка, маса якої , з тонким однорідним стрижнем, що має масу
 і довжину
,
якщо вони лежать на одній прямій і
ближній кінець стрижня розміщується
на відстані
від частинки?
і довжину
,
якщо вони лежать на одній прямій і
ближній кінець стрижня розміщується
на відстані
від частинки?
Як змінюється прискорення вільного падіння з висотою над поверхнею Землі і глибиною ? В обох випадках відстань відраховується від поверхні Землі. Вважати, що Земля є однорідною кулею.
Космічний корабель обертається по коловій орбіті навколо Землі на висоті
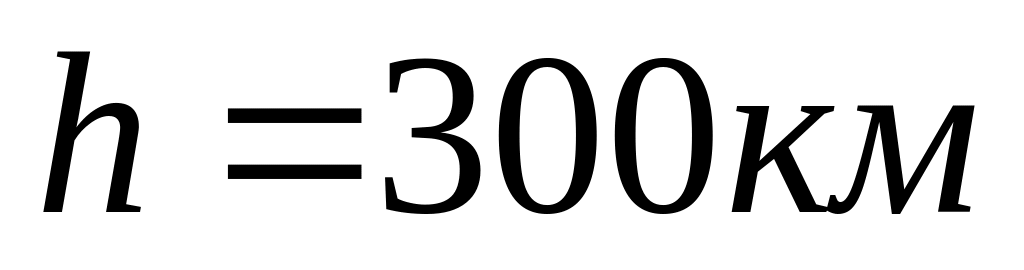 над її поверхнею. Визначити швидкість
корабля, а також вагу
і силу тяжіння
над її поверхнею. Визначити швидкість
корабля, а також вагу
і силу тяжіння
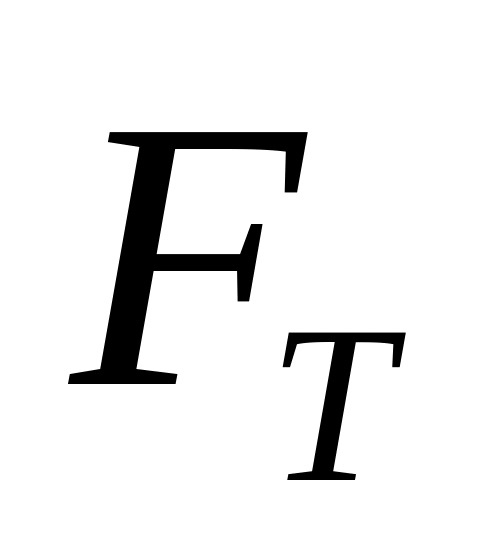 ,
що діють на космонавта, маса якого
,
що діють на космонавта, маса якого
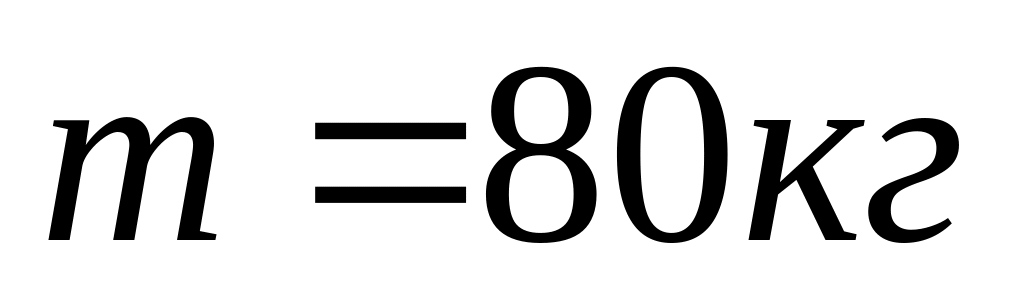 .
.
Космонавт, маса якого
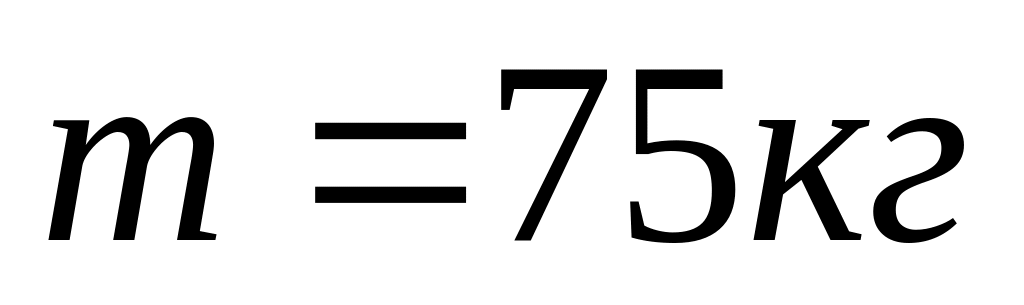 ,
перебуває в центрифузі, що обертається
навколо вертикальної осі з кутовою
швидкістю
,
перебуває в центрифузі, що обертається
навколо вертикальної осі з кутовою
швидкістю
 .
Радіус центрифуги
.
Визначити числове значення і напрям
ваги
космонавта.
.
Радіус центрифуги
.
Визначити числове значення і напрям
ваги
космонавта.
Тіло масою прикріплено до двох послідовно з’єднаних пружин із жорсткостями
 і
і
 .
До вільного кінця ланцюжка пружин
прикладена постійна сила
.
Яким буде сумарне подовження пружин?
.
До вільного кінця ланцюжка пружин
прикладена постійна сила
.
Яким буде сумарне подовження пружин?
Мідний стержень затиснуто між двома опорами. Його температуру збільшили на
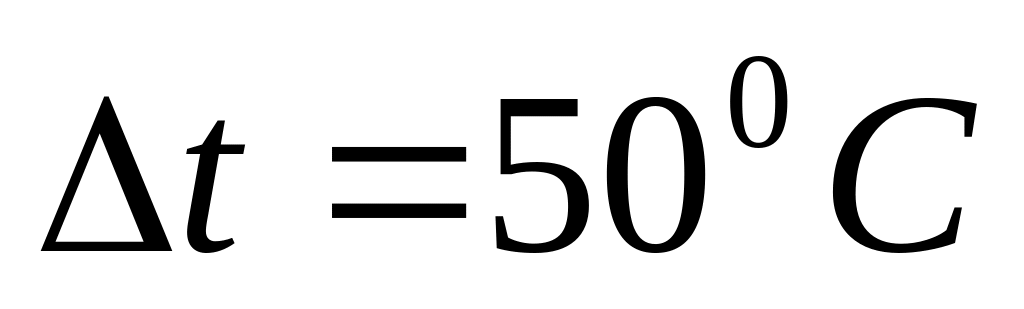 .
Яке напруження
.
Яке напруження
 виникає в стержні? Модуль Юнга для міді
виникає в стержні? Модуль Юнга для міді
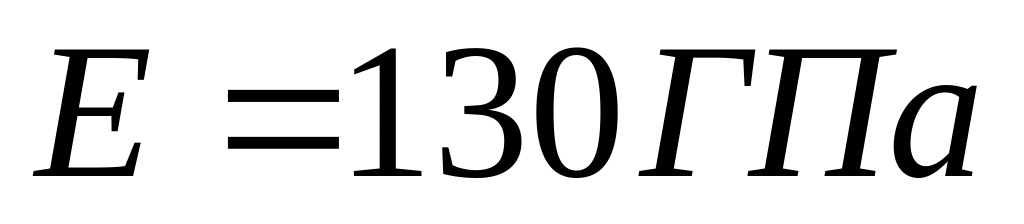 .
Температурний коефіцієнт лінійного
розширення міді
.
Температурний коефіцієнт лінійного
розширення міді
 .
.
Стержень, що має густину , довжину і площу поперечного перерізу , стоїть на горизонтальній поверхні. На скільки зменшиться його довжина і об’єм під дією власної маси?
Сталевий стержень, маса якого
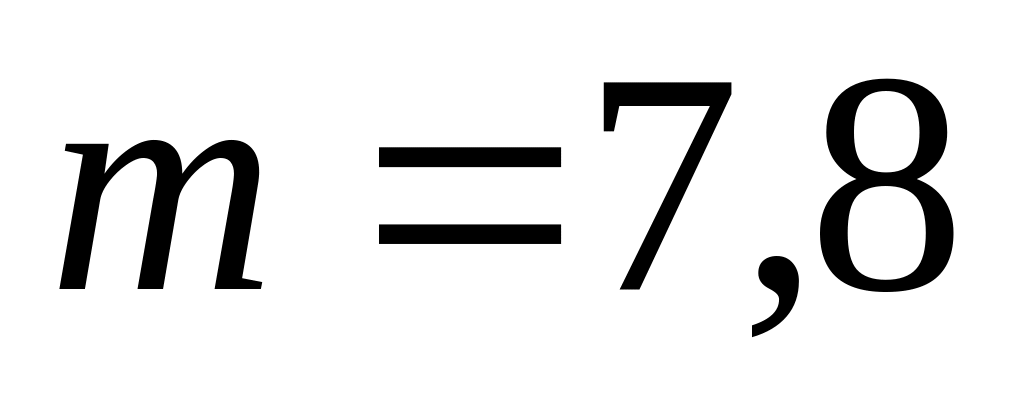
 ,
довжина
,
довжина
 ,
обертається навколо осі, що проходить
через його середину, з кутовою швидкістю
,
обертається навколо осі, що проходить
через його середину, з кутовою швидкістю
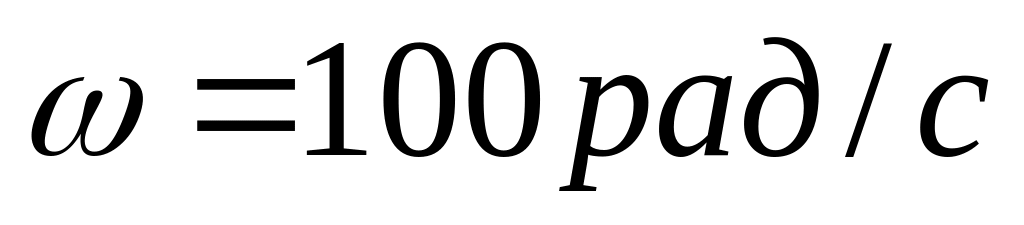 .
Визначити найбільші напруження
.
Визначити найбільші напруження
 в стержні, якщо площа його поперечного
перерізу
в стержні, якщо площа його поперечного
перерізу
 .
.
Дві пружини з коефіцієнтами жорсткості і з’єднують один раз послідовно, другий – паралельно. Якої жорсткості
 треба взяти пружини, щоб ними можна
було замінити у кожному випадку ці
системи з двох пружин?
треба взяти пружини, щоб ними можна
було замінити у кожному випадку ці
системи з двох пружин?
Як зміниться жорсткість пружини, якщо її довжину зменшити у разів?
Визначити час
 підйому тіла, маса якого
,
кинутого вгору зі швидкістю
.
Вважати, що сила опору руху залежить
від швидкості за законом
підйому тіла, маса якого
,
кинутого вгору зі швидкістю
.
Вважати, що сила опору руху залежить
від швидкості за законом
 .
.
Чавунне ядро масою падає у воді з постійною швидкістю . З якою силою
 треба тягти його вгору, щоб воно
піднімалося з постійною швидкістю
треба тягти його вгору, щоб воно
піднімалося з постійною швидкістю
 .
Вважайте, що сила опору води прамо
пропорційна модулю швидкості.
.
Вважайте, що сила опору води прамо
пропорційна модулю швидкості.
На барабан радіусом
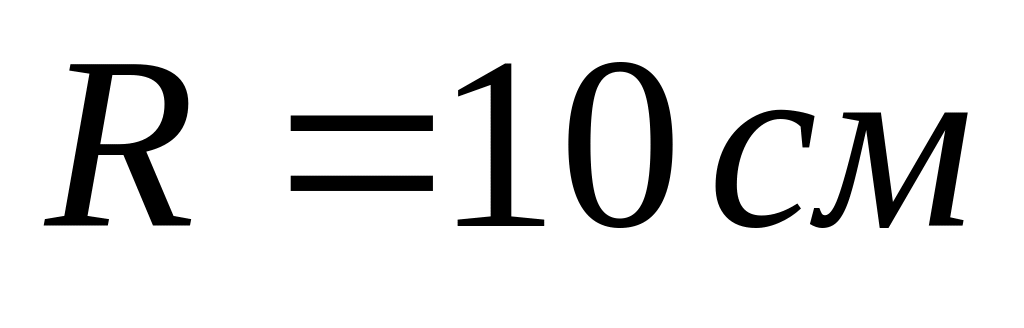 намотана нитка, до кінця якої прив’язаний
вантаж масою
намотана нитка, до кінця якої прив’язаний
вантаж масою
 .
Знайти момент інерції
барабана, якщо вантаж опускається з
прискоренням
.
Знайти момент інерції
барабана, якщо вантаж опускається з
прискоренням
 .
.
Куля скочується по похилій площині з кутом нахилу . Яку швидкість буде мати центр кулі відносно похилої площини через
 ,
якщо її початкова швидкість була рівна
нулю?
,
якщо її початкова швидкість була рівна
нулю?
Знайти кінетичну енергію диска масою , що котиться без ковзання по горизонтальній поверхні з лінійною швидкістю
 .
.
Яку роботу потрібно виконати, щоб маховику у вигляді диска масою
 і
радіусом
і
радіусом
 надати частоту обертання
надати частоту обертання
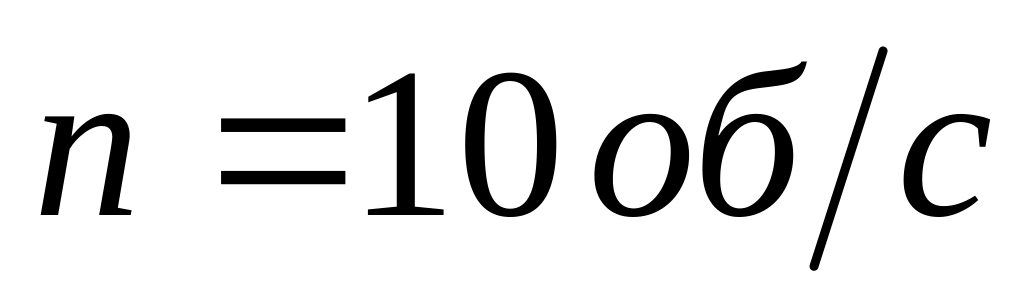 ,
якщо він знаходиться в стані спокою?
,
якщо він знаходиться в стані спокою?
Куля та суцільний циліндр, виготовлені з одного й того ж матеріалу, однакової маси котяться без ковзання з однаковою швидкістю. Як відносяться їх кінетичні енергії?
Повна кінетична енергія диска, що котиться по горизонтальній поверхні, рівна
 .
Обчислити кінетичну енергію
.
Обчислити кінетичну енергію
 поступального та
поступального та
 обертального руху диска.
обертального руху диска.
До обода однорідного суцільного диска масою
 ,
насадженого на вісь, прикладена постійна
дотична сила
,
насадженого на вісь, прикладена постійна
дотична сила
 .
Обчислити кінетичну енергію диска
через час
.
Обчислити кінетичну енергію диска
через час
 після початку дії сили.
після початку дії сили.
Вентилятор обертається з частотою
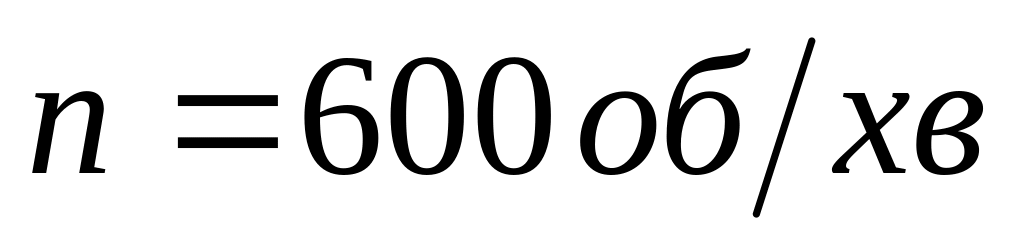 .
Після виключення він почав обертатись
рівносповільнено і, зробивши
.
Після виключення він почав обертатись
рівносповільнено і, зробивши
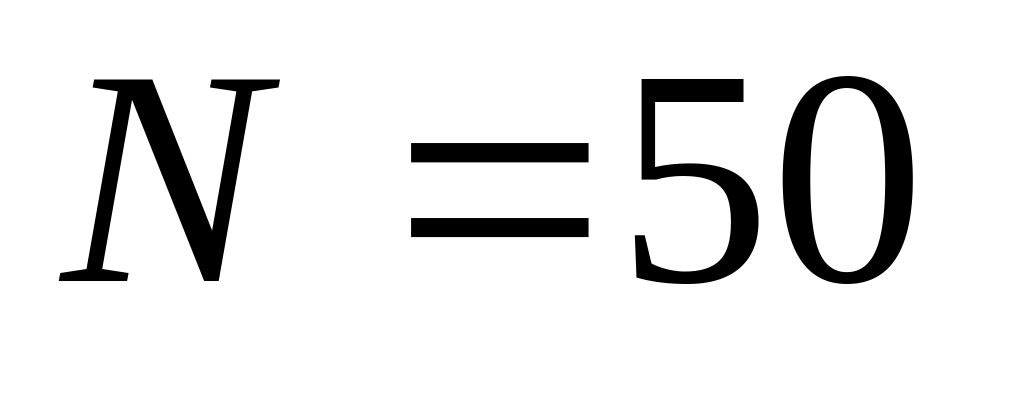 обертів,
зупинився. Робота сил гальмування
обертів,
зупинився. Робота сил гальмування
 .
Обчислити:
1) момент сил
гальмування; 2) момент інерції вентилятора.
.
Обчислити:
1) момент сил
гальмування; 2) момент інерції вентилятора.
Маховик у вигляді суцільного диска, момент інерції якого рівний
 ,
обертається з частотою
,
обертається з частотою
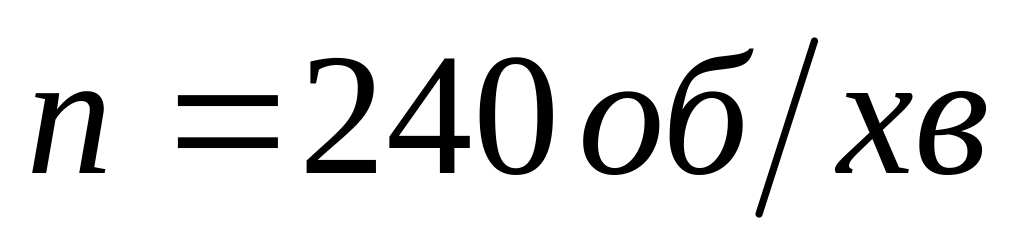 .
Через час
.
Через час
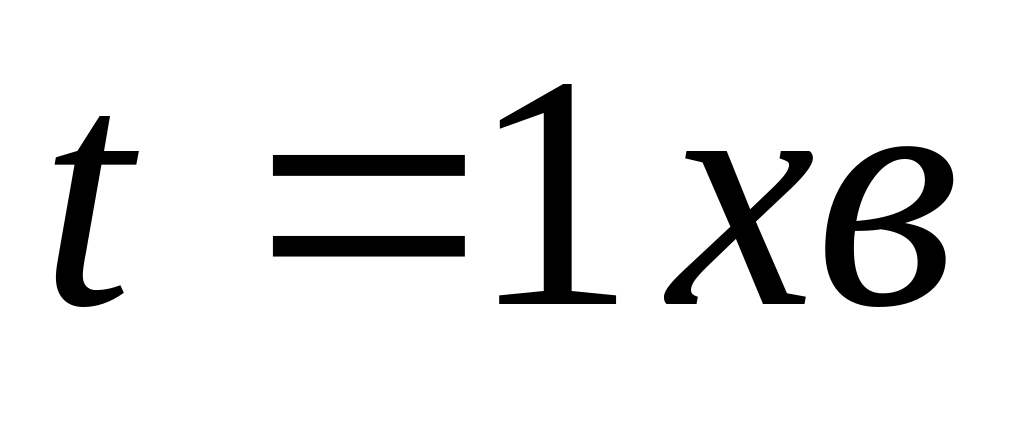 ,
як на маховик став діяти момент сили
гальмування, він зупинився. Знайти:
1) момент сил
гальмування;
2) кількість
обертів маховика від початку гальмування
до повної зупинки.
,
як на маховик став діяти момент сили
гальмування, він зупинився. Знайти:
1) момент сил
гальмування;
2) кількість
обертів маховика від початку гальмування
до повної зупинки.
До обода однорідного суцільного диска радіусом
 прикладена постійна дотична сила
прикладена постійна дотична сила
 .
При обертанні диска на нього діє момент
сил тертя
.
При обертанні диска на нього діє момент
сил тертя
 .
Обчислити масу
диска, якщо відомо, що його кутове
прискорення
постійне і рівне
.
Обчислити масу
диска, якщо відомо, що його кутове
прискорення
постійне і рівне
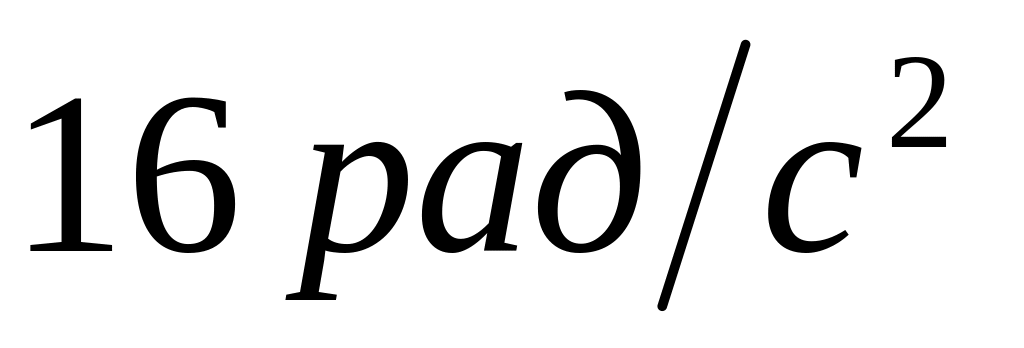 .
.
Частота обертання
 маховика, момент інерції якого рівний
маховика, момент інерції якого рівний
 ,
складає
,
складає
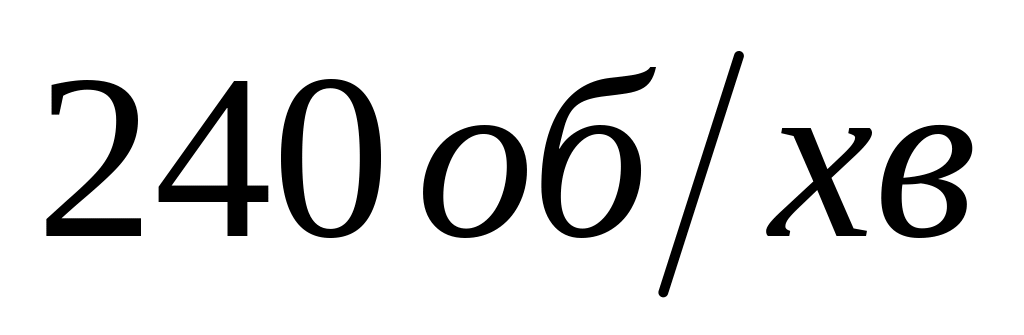 .
Після закінчення дії на нього обертального
моменту маховик під дією сил тертя в
підшипниках зупинився за час
.
Після закінчення дії на нього обертального
моменту маховик під дією сил тертя в
підшипниках зупинився за час
 .
Якщо вважати тертя в підшипниках
постійним, знайти момент сил тертя
.
.
Якщо вважати тертя в підшипниках
постійним, знайти момент сил тертя
.
Маховик у вигляді суцільного диска, момент інерції якого рівний
 ,
обертаючись при гальмуванні
рівносповільнено, за час
зменшив частоту свого обертання з
,
обертаючись при гальмуванні
рівносповільнено, за час
зменшив частоту свого обертання з
 до
до
 .
Знайти:
1) кутове прискорення маховика
;
2) момент
сил
гальмування;
3) роботу гальмування
.
.
Знайти:
1) кутове прискорення маховика
;
2) момент
сил
гальмування;
3) роботу гальмування
.
На однорідний суцільний циліндричний вал радіусом
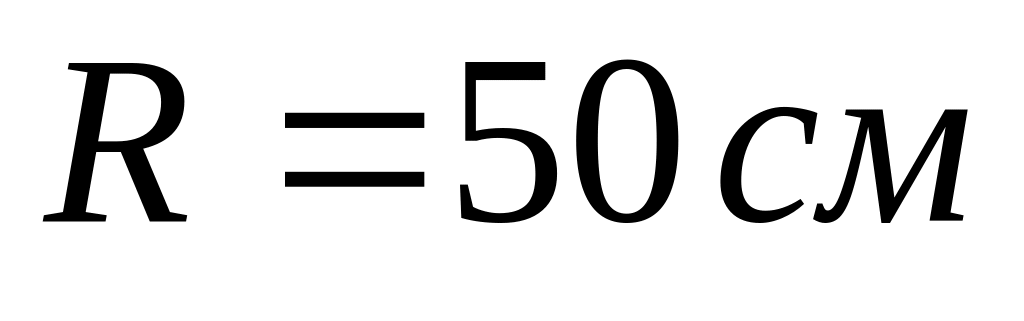 намотана легка нитка, до кінця якої
прикріплений вантаж масою
намотана легка нитка, до кінця якої
прикріплений вантаж масою
 .
Вантаж, розмотуючи нитку, опускається
з прискоренням
.
Вантаж, розмотуючи нитку, опускається
з прискоренням
 .
Знайти:
1) момент інерції
вала;
2) масу
вала.
.
Знайти:
1) момент інерції
вала;
2) масу
вала.
На однорідний суцільний циліндричний вал радіусом
 ,
момент інерції якого
,
момент інерції якого
 ,
намотана легка нитка, до кінця якої
прикріплений вантаж масою
,
намотана легка нитка, до кінця якої
прикріплений вантаж масою
 .
До початку обертання вала висота
вантажа над підлогою становила
.
До початку обертання вала висота
вантажа над підлогою становила
 .
Знайти:
1) час опускання вантажа до підлоги;
2) силу
натягу нитки;
3) кінетичну
енергію вантажу в момент удару об
підлогу.
.
Знайти:
1) час опускання вантажа до підлоги;
2) силу
натягу нитки;
3) кінетичну
енергію вантажу в момент удару об
підлогу.
Через нерухомий блок у вигляді суцільного циліндра масою
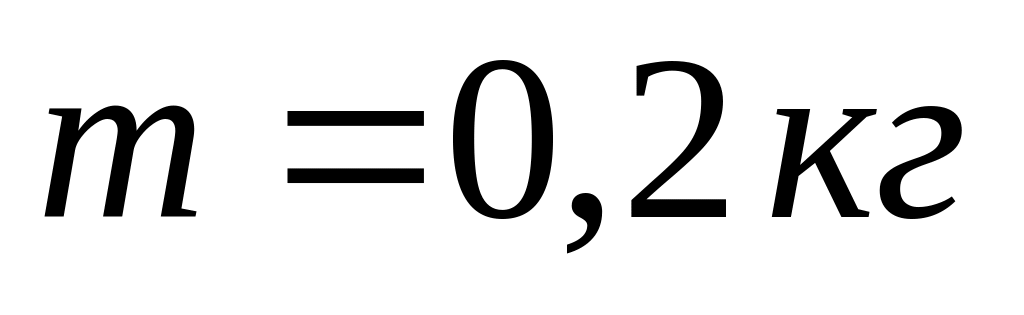 перекинута невагома нитка, до кінців
якої прикріплені тіла масами
перекинута невагома нитка, до кінців
якої прикріплені тіла масами
 та
та
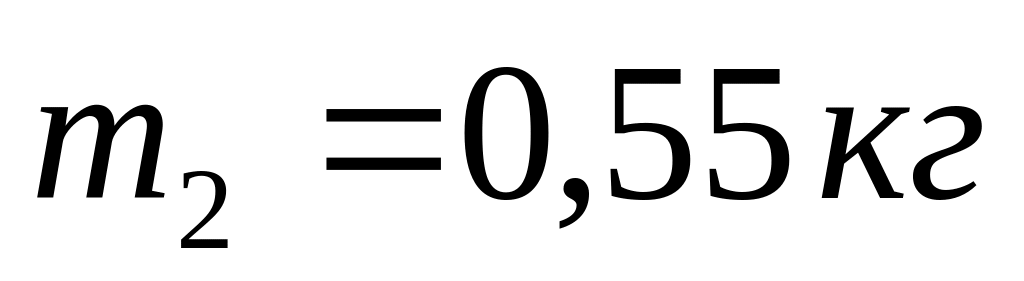 .
Нехтуючи тертям у вісі блока, знайти:
1) прискорення тіл;
2) відношення
.
Нехтуючи тертям у вісі блока, знайти:
1) прискорення тіл;
2) відношення
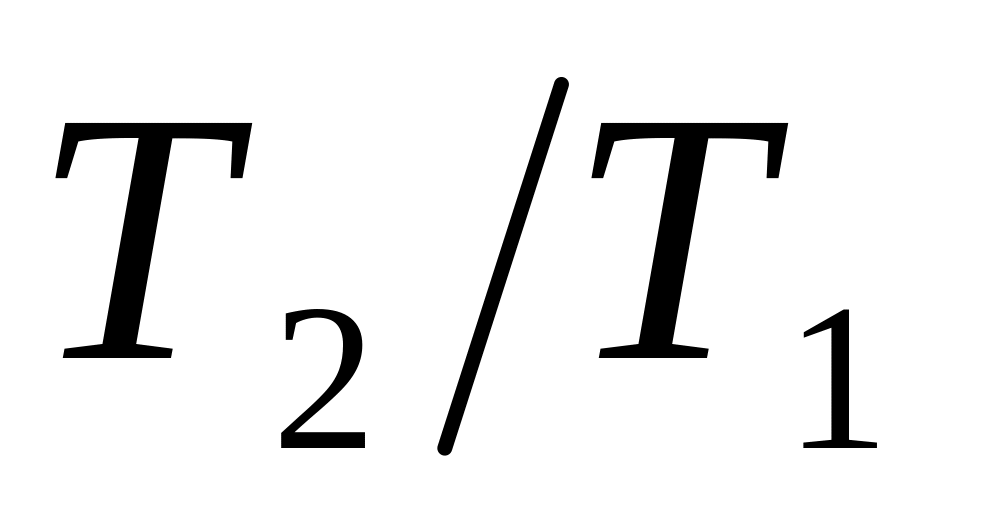 сил
натягу нитки.
сил
натягу нитки.
Маховик починає обертатися зі стану спокою з постійним кутовим прискоренням
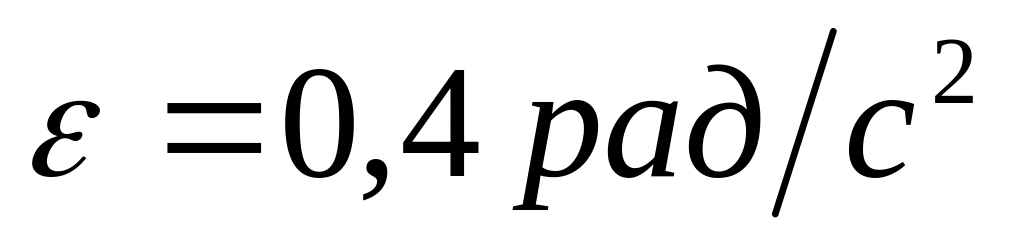 .
Знайти кінетичну енергію маховика
через час
.
Знайти кінетичну енергію маховика
через час
 від початку руху, якщо через
від початку руху, якщо через
 від початку руху момент імпульсу
маховика
від початку руху момент імпульсу
маховика
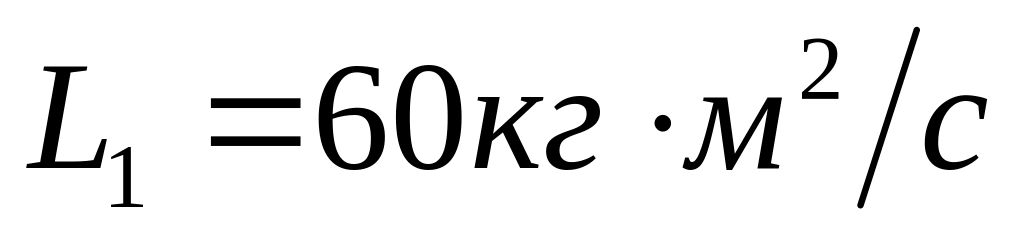 .
.
Горизонтальна платформа у вигляді диска обертається з частотою
 .
У центрі платформи стоїть людина і
тримає у розставлених руках гирі. Знайти
частоту обертання платформи, якщо
людина, опустивши руки, зменшить свій
момент інерції від
.
У центрі платформи стоїть людина і
тримає у розставлених руках гирі. Знайти
частоту обертання платформи, якщо
людина, опустивши руки, зменшить свій
момент інерції від
 до
до
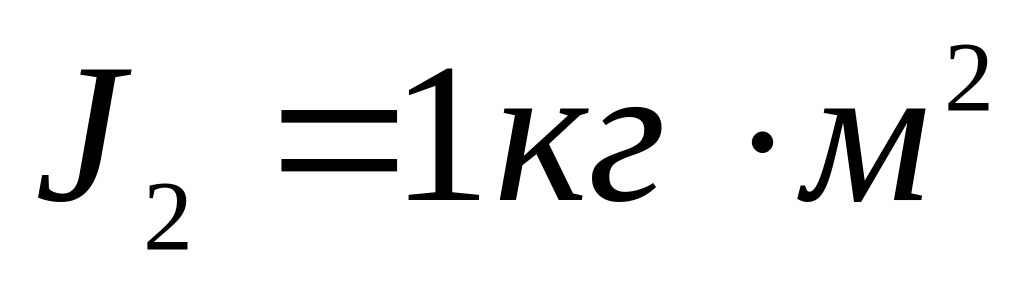 .
Маса платформи
.
Маса платформи
 ,
її радіус
,
її радіус
 .
.
Маховик, насаджений на горизонтальний вал, може легко обертатися. На циліндричну поверхню маховика, що має радіус
 ,
намотали
нитку, до вільного кінця якої підвісили
вантаж масою
,
намотали
нитку, до вільного кінця якої підвісили
вантаж масою
 ,
і відпустили. Вантаж почав опускатися,
приводячи маховик в обертання, і за
,
і відпустили. Вантаж почав опускатися,
приводячи маховик в обертання, і за
 пройшов шлях
пройшов шлях
 .
Знайти момент інерції маховика.
.
Знайти момент інерції маховика.
Маховик у вигляді диска масою
 і радіуса
і радіуса
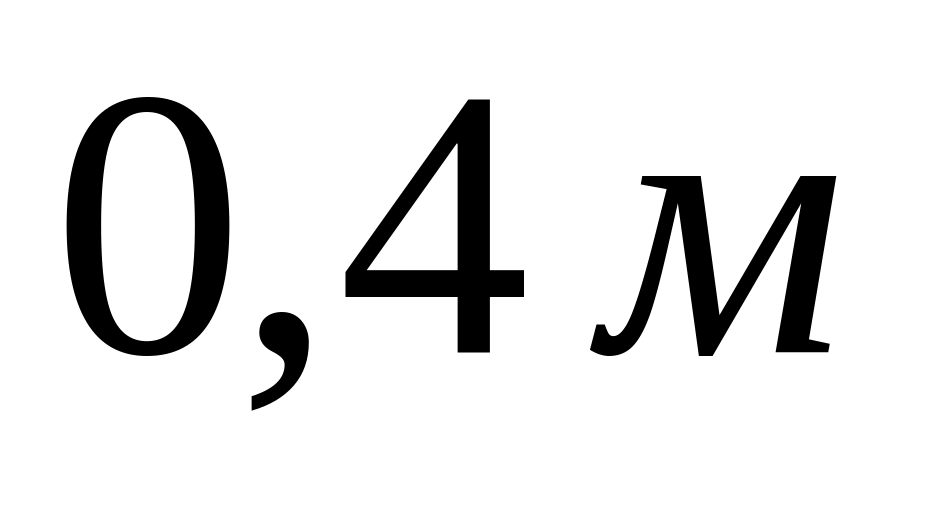 ,
обертається,
здійснюючи
,
обертається,
здійснюючи
 .
Після початку гальмування маховик
зупинився через
.
Знайти момент сил тертя, який сповільнив
обертання маховика.
.
Після початку гальмування маховик
зупинився через
.
Знайти момент сил тертя, який сповільнив
обертання маховика.
Маховик у вигляді циліндра масою
 і радіуса
і радіуса
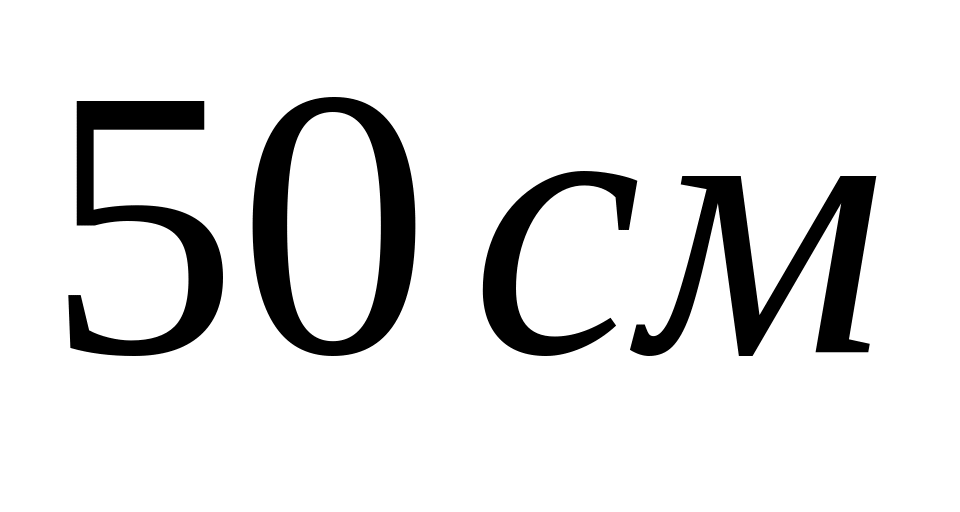 ,
обертається, здійснюючи
,
обертається, здійснюючи
 .
На циліндричну поверхню маховика почала
діяти гальмуюча сила в
.
На циліндричну поверхню маховика почала
діяти гальмуюча сила в
 .
Скільки обертів зробить маховик до
зупинки?
.
Скільки обертів зробить маховик до
зупинки?
Чому рівний момент інерції тонкого прямого стержня довжиною
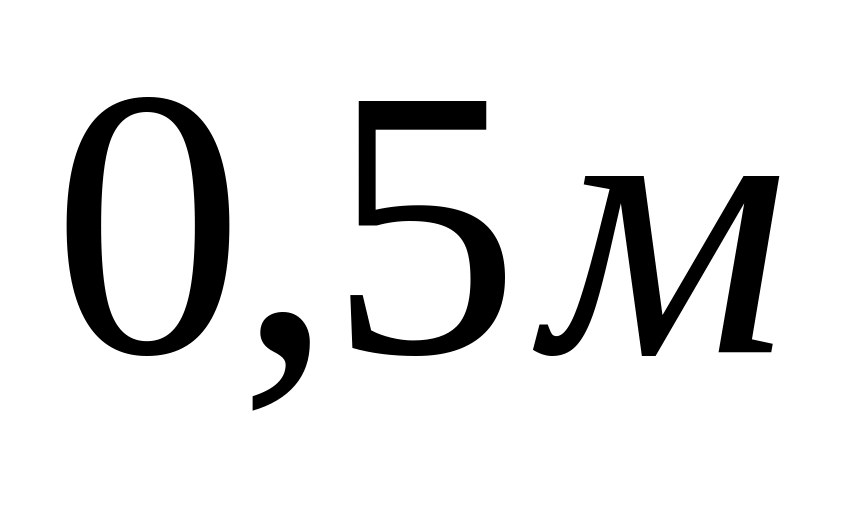 і масою
і масою
 відносно вісі, перпендикулярної до
його довжини і яка проходить через
точку стержня, що віддалена на
відносно вісі, перпендикулярної до
його довжини і яка проходить через
точку стержня, що віддалена на
 від одного із його кінців?
від одного із його кінців?
Маховик, що являє собою диск масою
 і радіуса
і радіуса
 ,
вільно обертається навколо вісі, яка
проходить через центр, з круговою
частотою
,
вільно обертається навколо вісі, яка
проходить через центр, з круговою
частотою
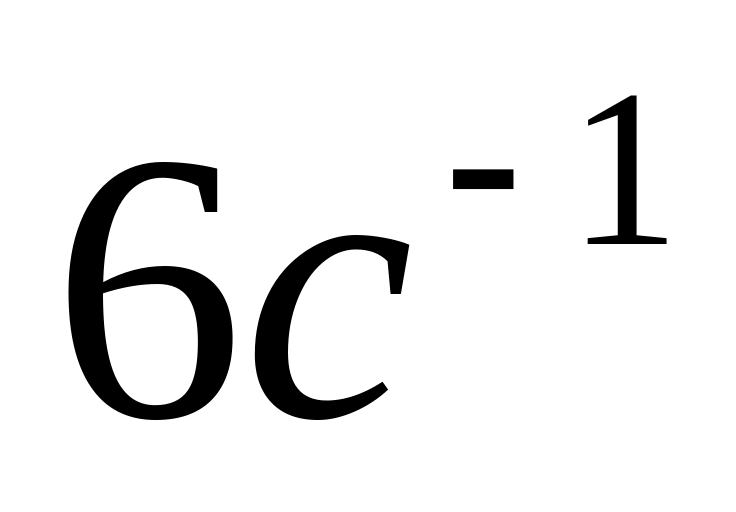 .
При гальмуванні маховик зупиняється
через
.
При гальмуванні маховик зупиняється
через
 .
Визначити гальмівний момент.
.
Визначити гальмівний момент.
Дві кулі однакового розміру, виготовлені з алюмінію і міді, обертаються незалежно одна від одної навколо загальної нерухомої осі, яка проходить через їх центри, з кутовими швидкостями
 і
і
 .
З якою кутовою швидкістю обертались
обидві кулі, якби їх жорстко з’єднали?
.
З якою кутовою швидкістю обертались
обидві кулі, якби їх жорстко з’єднали?
Нитка з прив’язаними до її кінців вантажами масами
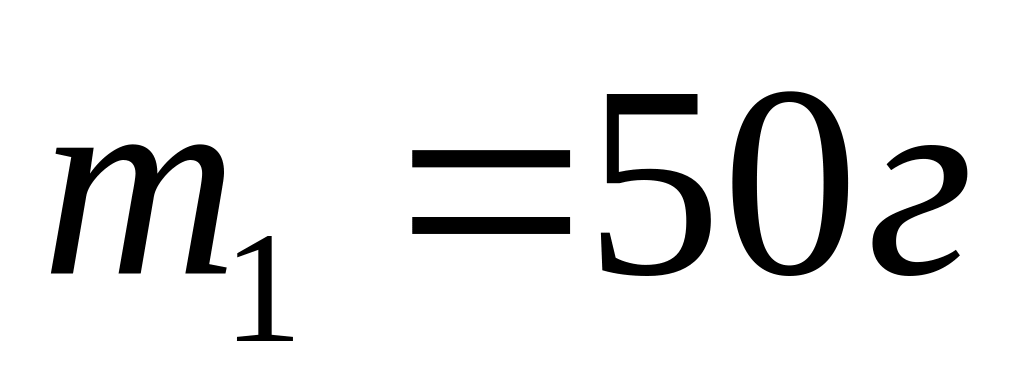 і
і
 перекинута через блок діаметром
перекинута через блок діаметром
 .
Визначити момент інерції
.
Визначити момент інерції блоку, якщо під дією сили тяжіння
вантажів він отримав кутове прискорення
блоку, якщо під дією сили тяжіння
вантажів він отримав кутове прискорення
 .
Тертям і ковзанням нитки по блоку
знехтувати.
.
Тертям і ковзанням нитки по блоку
знехтувати.
Стержень обертається навколо вісі, яка проходить через його середину, згідно рівнянню
 ,
де
,
де
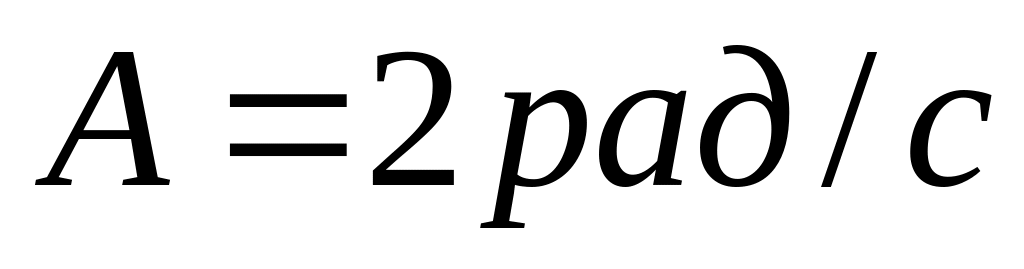 ,
,
 .
Визначити момент обертання
,
що діє на стержень через час
.
Визначити момент обертання
,
що діє на стержень через час
 після початку обертання, якщо момент
інерції стержня
після початку обертання, якщо момент
інерції стержня
 .
.
По горизонтальній площині котиться диск зі швидкістю
 .
Визначити коефіцієнт опору, якщо диск,
будучи наданим самому собі, зупинився,
пройшовши шлях
.
Визначити коефіцієнт опору, якщо диск,
будучи наданим самому собі, зупинився,
пройшовши шлях
 .
.
Визначити момент сили , який необхідно прикласти до блоку, який обертається з частотою
 ,
щоб він зупинився протягом часу
,
щоб він зупинився протягом часу
 .
Діаметр блоку
.
Діаметр блоку
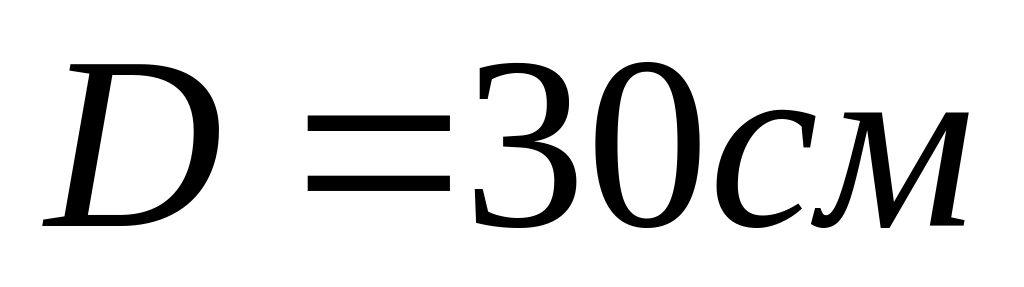 .
Масу блоку
.
Масу блоку
 вважати рівномірно розподіленою по
ободу.
вважати рівномірно розподіленою по
ободу.
Блок, який має форму диска масою
 ,
обертається під дією сили натягу нитки,
до кінців якої підвішені вантажі масами
,
обертається під дією сили натягу нитки,
до кінців якої підвішені вантажі масами
 і
і
 .
Визначити сили натягу
.
Визначити сили натягу
 і
і
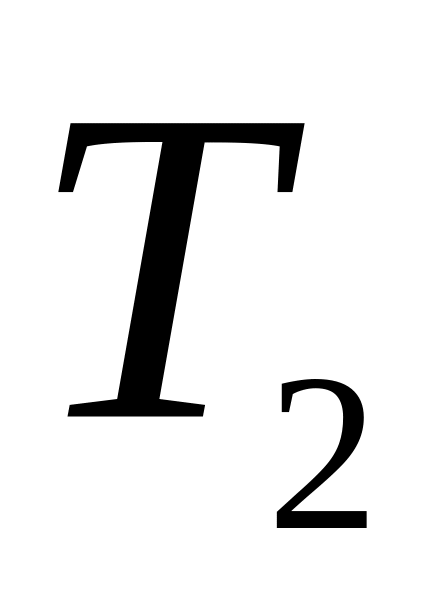 нитки по обидві сторони блоку.
нитки по обидві сторони блоку.
До кінців легкої і нерозтяжної нитки, перекинутої через блок, підвішені вантажі масами
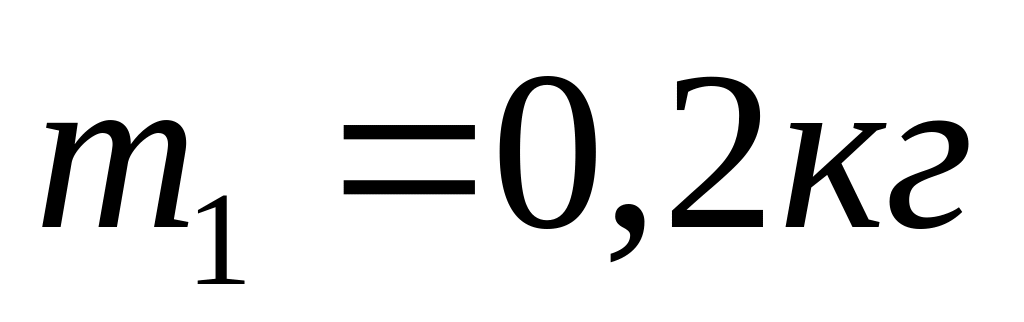 і
і
 .
У скільки разів відрізняються сили,
які діють на нитку по обидві сторони
від блоку, якщо маса блоку
,
а його вісь рухається вертикально вгору
з прискоренням
.
У скільки разів відрізняються сили,
які діють на нитку по обидві сторони
від блоку, якщо маса блоку
,
а його вісь рухається вертикально вгору
з прискоренням
 ?
Силами тертя і ковзанням нитки по блоку
знехтувати.
?
Силами тертя і ковзанням нитки по блоку
знехтувати.
Виведіть формулу для визначення моменту інерції тонкого однорідного стержня, маса якого і довжина , відносно вісі, що приходить: а) через центр мас стержня перпендикулярно до нього; б) паралельно стержню на відстань від нього.
Конічний маятник, маса якого , підвішений на нитці завдовжки
 і обертається з кутовою швидкістю
і обертається з кутовою швидкістю
 ,
описуючи конус з кутом розхилу
,
описуючи конус з кутом розхилу
 .
Визначити момент імпульсу
.
Визначити момент імпульсу
 маятника відносно точки підвісу і
вказати його напрям у просторі.
маятника відносно точки підвісу і
вказати його напрям у просторі.
До одного кінця нитки, перекинутої через блок, підвішений вантаж, маса якого
 .
До другого її кінця прикладена донизу
сила
.
До другого її кінця прикладена донизу
сила
 ,
де
,
де
 ,
,
 ,
–
час, с. Блок має форму диска, його маса
.
З якими прискореннями
і
рухатимиться вантаж через час
,
–
час, с. Блок має форму диска, його маса
.
З якими прискореннями
і
рухатимиться вантаж через час
 і
і
 від початку дії сили?
від початку дії сили?
Маховик, маса якого , жорстко зв’язаний зі шківом радіуса
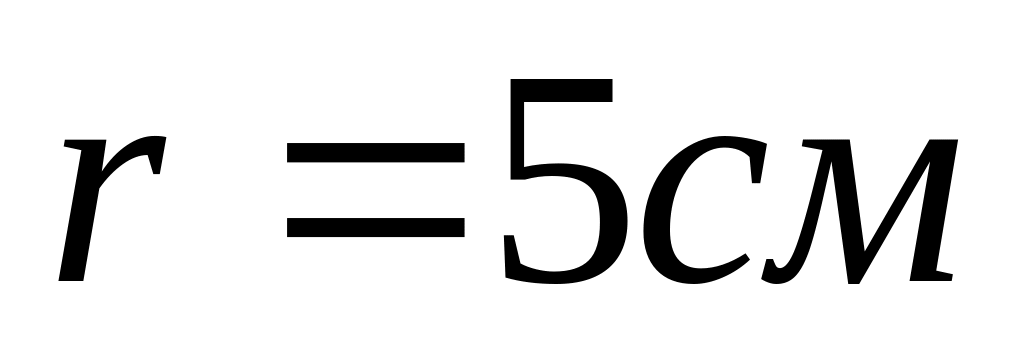 .
Маса шківа
.
Маса шківа
 .
Система приводиться в рух за допомогою
тягарця, маса якого
.
Система приводиться в рух за допомогою
тягарця, маса якого
 .
Тягарець прив’язаний до одного з кінців
мотузки, що намотана на шків. Визначити
частоту
.
Тягарець прив’язаний до одного з кінців
мотузки, що намотана на шків. Визначити
частоту
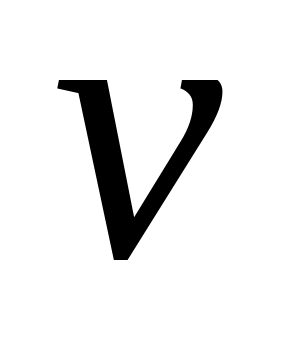 обертання маховика через перші
обертання маховика через перші
 руху. Вважати, що вся маса маховика
розподілена по ободу на відстані
руху. Вважати, що вся маса маховика
розподілена по ободу на відстані
 від осі обертання.
від осі обертання.
Тонка сферична оболонка, масою і радіуса
 ,
обертається з частотою
,
обертається з частотою
 навколо своєї вісі симетрії. Визначити
момент імпульсу
навколо своєї вісі симетрії. Визначити
момент імпульсу
 оболонки відносно цієї вісі.
оболонки відносно цієї вісі.
Автоматна куля у вигляді циліндра, діаметр якої
 ,
а маса
,
а маса
 ,
обертається навколо своєї вісі з кутовою
швидкістю
,
обертається навколо своєї вісі з кутовою
швидкістю
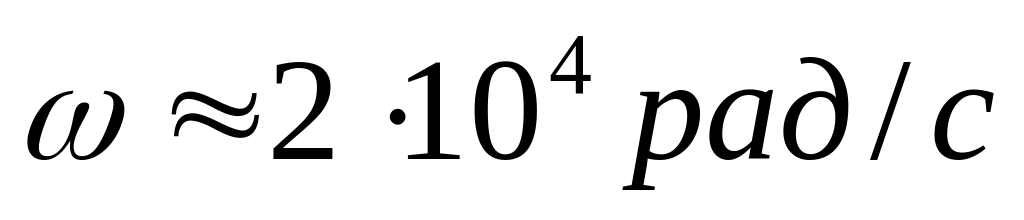 .
Визначити момент імпульсу
кулі відносно вісі.
.
Визначити момент імпульсу
кулі відносно вісі.
Куля, радіус якої
 і маса
,
обертається навколо своєї вісі згідно
з рівнянням
і маса
,
обертається навколо своєї вісі згідно
з рівнянням
 ,
де
,
де
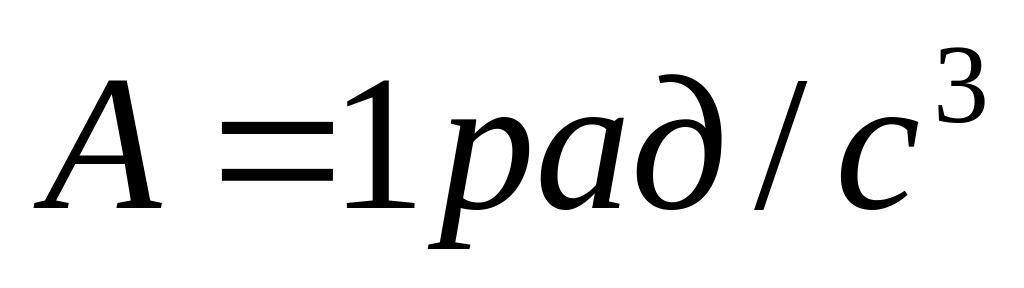 ,
,
 .
Визначити момент сили
для моментів часу
і
.
.
Визначити момент сили
для моментів часу
і
.
Однорідний суцільний диск радіуса може обертатися навколо вертикальної вісі, яка збігається з його віссю симетрії. До ободу диска прикладена дотична сила
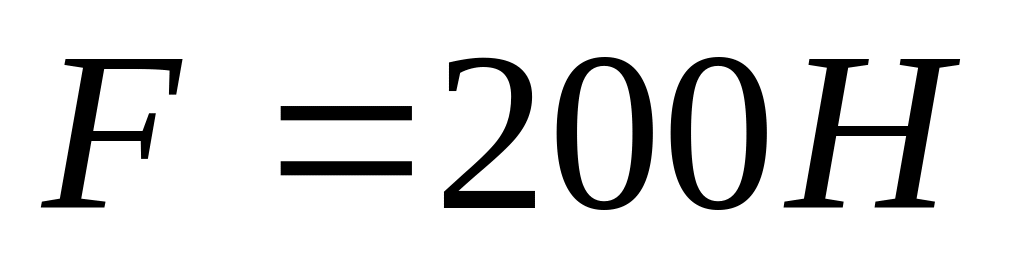 .
Визначити масу
диска, якщо його кутове прискорення
.
Визначити масу
диска, якщо його кутове прискорення
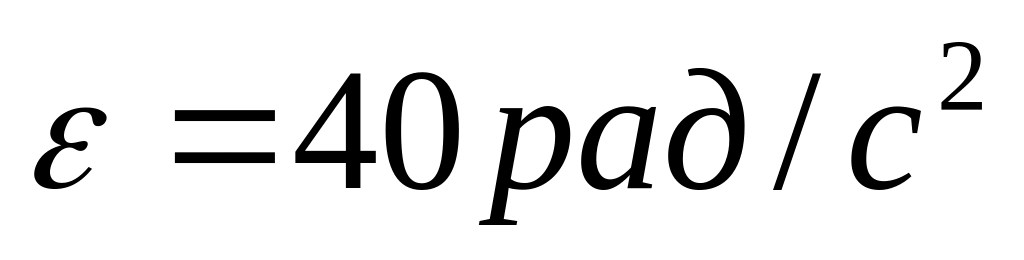 ,
а момент сили тертя, що діє при обертанні
диска,
,
а момент сили тертя, що діє при обертанні
диска,
 .
.
Суцільний циліндр, маса якого і радіус , обертається навколо своєї вісі згідно закону
 .
Як залежать від часу момент
сили, що діє на циліндр, і момент імпульсу
циліндра?
.
Як залежать від часу момент
сили, що діє на циліндр, і момент імпульсу
циліндра?
Тонкий обруч, маса якого
 і радіус
і радіус
 ,
котиться без проковзування зі швидкістю
по горизонтальній поверхні. Визначити
модуль моменту імпульсу
обруча відносно точки торкання його з
поверхнею (відносно миттєвого вісі
обертання).
,
котиться без проковзування зі швидкістю
по горизонтальній поверхні. Визначити
модуль моменту імпульсу
обруча відносно точки торкання його з
поверхнею (відносно миттєвого вісі
обертання).
Гіроскоп, що має форму диска радіуса
 ,
обертається навколо своєї вісі симетрії
з частотою
,
обертається навколо своєї вісі симетрії
з частотою
 .
Вісь гіроскопа утворює деякий кут
з вертикаллю і може вільно повертатися
навколо точки
.
Вісь гіроскопа утворює деякий кут
з вертикаллю і може вільно повертатися
навколо точки
 .
Відстань
від точки
до центра мас гіроскопа
.
Відстань
від точки
до центра мас гіроскопа
 .
Обчислити кутову швидкість
.
Обчислити кутову швидкість
 обертання вісі гіроскопа навколо
вертикалі (кутову швидкість прецесії).
Як залежить кутова швидкість
прецесії від кута
нахилу вісі гіроскопа?
обертання вісі гіроскопа навколо
вертикалі (кутову швидкість прецесії).
Як залежить кутова швидкість
прецесії від кута
нахилу вісі гіроскопа?
Мінімальна робота, необхідна для кидання тіла на відстань
 ,
дорівнює
,
дорівнює
 .
Знайти масу тіла.
.
Знайти масу тіла.
Людина масою
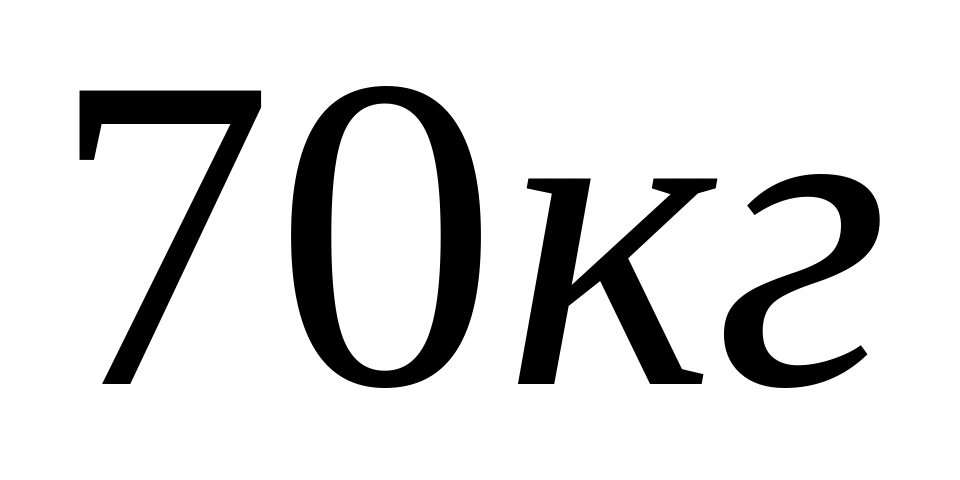 біжить зі швидкістю
біжить зі швидкістю
 ,
доганяє візок масою
,
доганяє візок масою
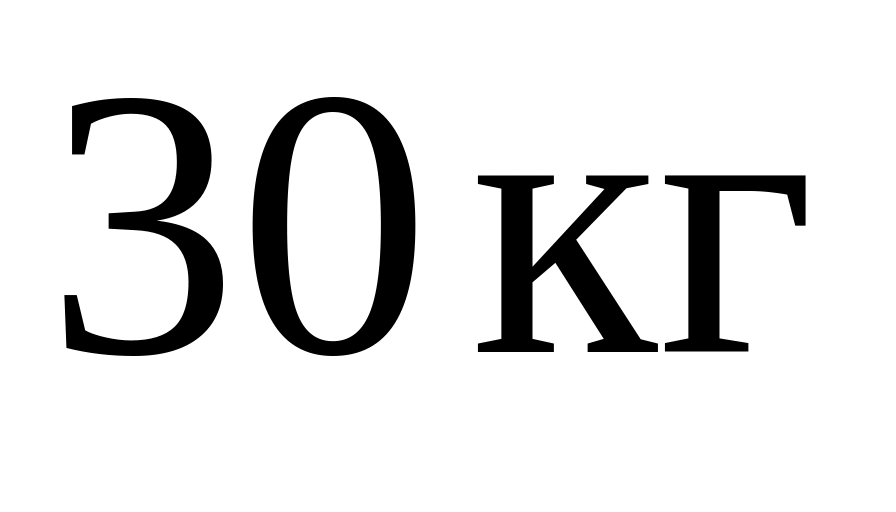 ,
що рухається зі швидкістю
,
і стрибає на нього. З якою швидкістю
рухатиметься візок після цього?
,
що рухається зі швидкістю
,
і стрибає на нього. З якою швидкістю
рухатиметься візок після цього?
Якої швидкості відносно води набуде нерухомий човен, маса якого з вантажем
 ,
коли пасажир, що сидить у човні, зробить
постріл у напрямі корми? Маса кулі
,
коли пасажир, що сидить у човні, зробить
постріл у напрямі корми? Маса кулі
 ,
а початкова швидкість
,
а початкова швидкість
 .
.
Вагон масою
 ,
що рухався зі швидкістю
,
що рухався зі швидкістю
 ,
стикається з нерухомим вагоном масою
,
стикається з нерухомим вагоном масою
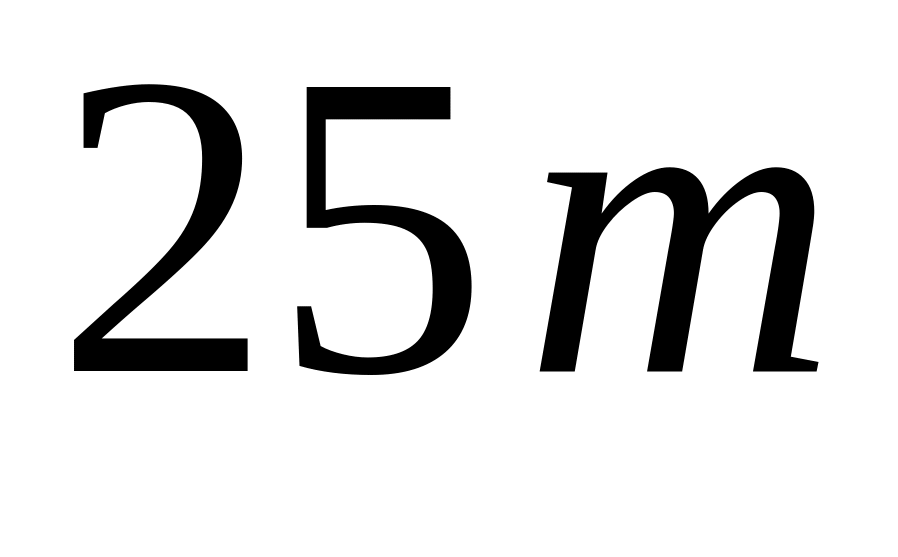 так, що спрацьовує механізм зчеплення.
Якою буде швидкість з’єднаних вагонів?
так, що спрацьовує механізм зчеплення.
Якою буде швидкість з’єднаних вагонів?
Тіло масою
 починає падати з висоти
починає падати з висоти
 .
Знайти суму потенціальної та кінетичної
енергії в точці, що знаходиться від
поверхні Землі на висоті
.
Знайти суму потенціальної та кінетичної
енергії в точці, що знаходиться від
поверхні Землі на висоті
 ,
якщо тіло має швидкість
,
якщо тіло має швидкість
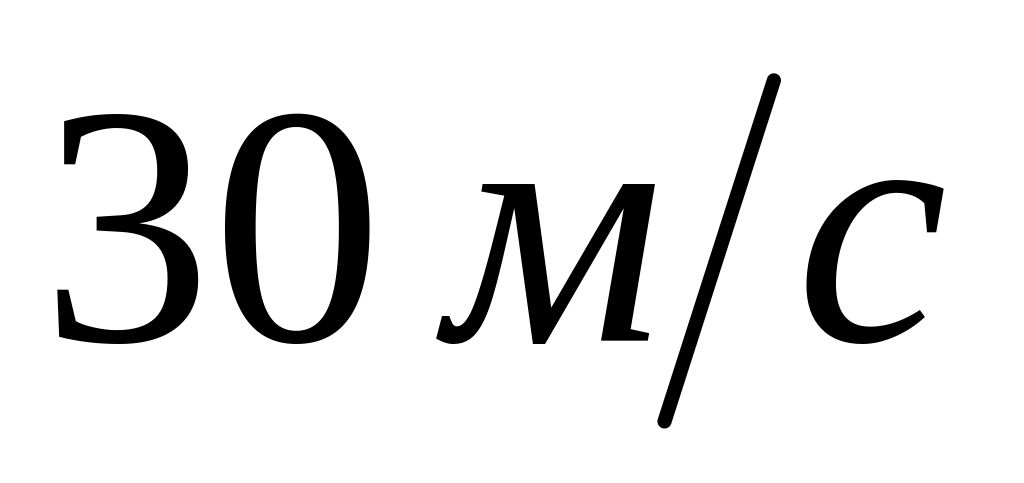 .
Тертям тіла об повітря знехтувати.
Порівняти цю енергію з початковою
енергією тіла.
.
Тертям тіла об повітря знехтувати.
Порівняти цю енергію з початковою
енергією тіла.
Тіло, що падало з певної висоти, в момент дотику до Землі має імпульс
 та кінетичну енергію
та кінетичну енергію
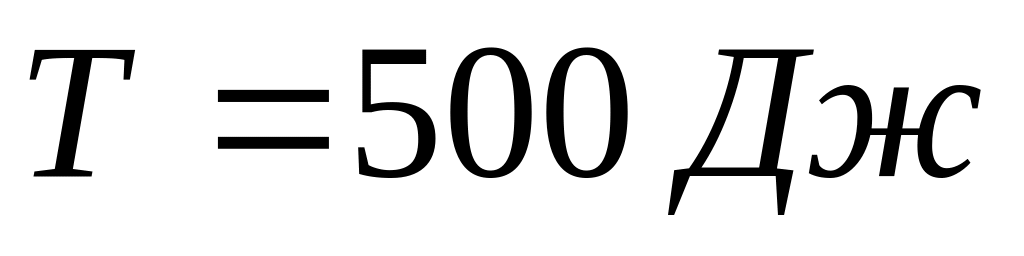 .
Знайти:
1) масу тіла; 2) висоту, з якої падало
тіло.
.
Знайти:
1) масу тіла; 2) висоту, з якої падало
тіло.
Матеріальна точка масою
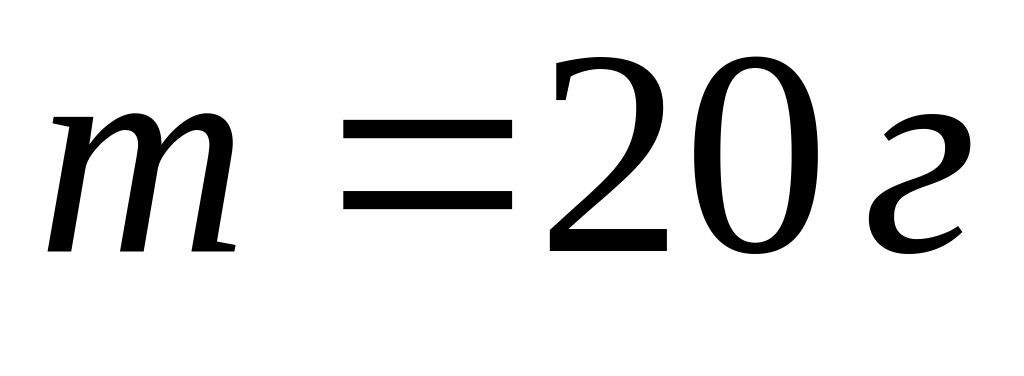 рухається по колу радіусом
з постійним тангенціальним прискоренням.
У кінці п’ятого оберту після початку
руху кінетична енергія матеріальної
точки стала рівною
рухається по колу радіусом
з постійним тангенціальним прискоренням.
У кінці п’ятого оберту після початку
руху кінетична енергія матеріальної
точки стала рівною
 .
Обчислити тангенціальне прискорення.
.
Обчислити тангенціальне прискорення.
Тіло кинули вертикально вгору зі швидкістю . Нехтуючи опором повітря, знайти на якій висоті кінетична енергія тіла буде рівна його потенціальній енергії.
Тіло, вагою
 ,
кинули з вежі вертикально вниз без
початкової швидкості. Знайти кінетичну
та потенціальну енергію у середній
точці шляху, якщо тіло падало
,
кинули з вежі вертикально вниз без
початкової швидкості. Знайти кінетичну
та потенціальну енергію у середній
точці шляху, якщо тіло падало
 .
Опором повітря знехтувати.
.
Опором повітря знехтувати.
Яку роботу потрібно виконати, щоб по похилій площині з кутом нахилу підняти вантаж масою
 на висоту
на висоту
 ,
якщо коефіцієнт тертя
,
якщо коефіцієнт тертя
 ?
?
Тіло масою
 ,
що падає з висоти
,
що падає з висоти
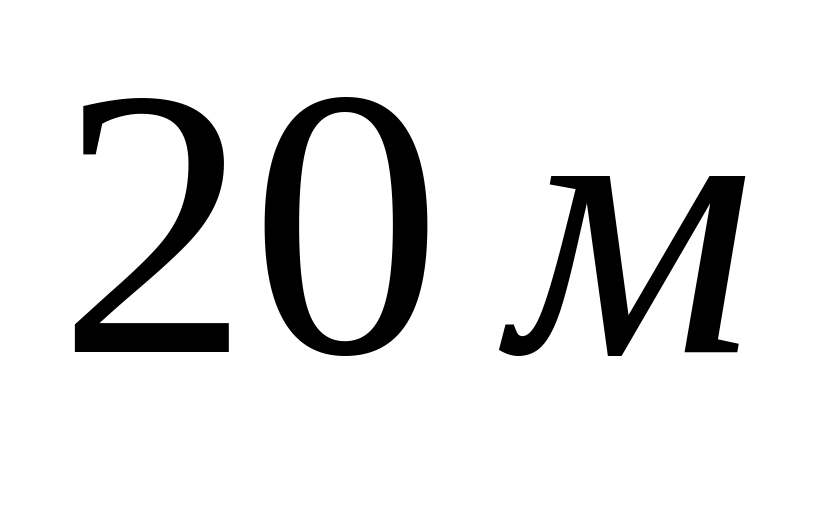 ,
проникає в м'який грунт на глибину
,
проникає в м'який грунт на глибину
 .
Визначити силу опору ґрунту.
.
Визначити силу опору ґрунту.
Автомобіль масою
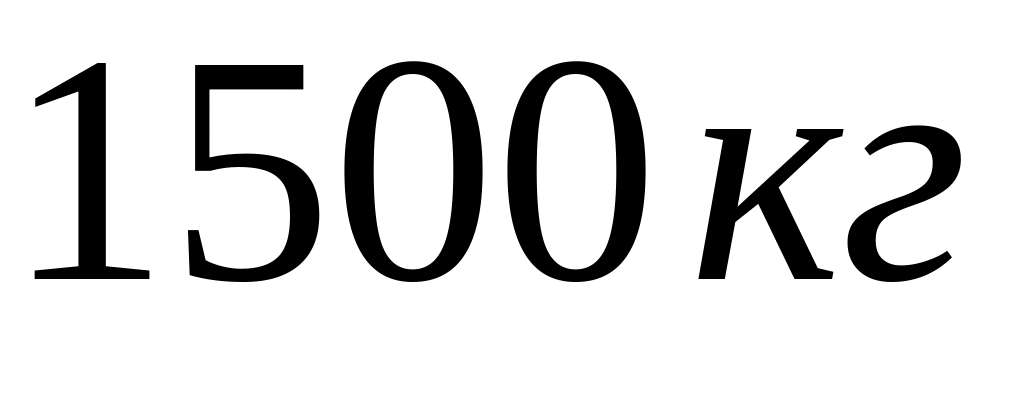 починає розгін із стану спокою по
горизонтальному шляху з прискоренням
починає розгін із стану спокою по
горизонтальному шляху з прискоренням
 .
Коефіцієнт опору рухові
.
Коефіцієнт опору рухові
 .
Знайти: 1) роботу, що виконується за
перші
руху; 2) середню потужність, що розвиває
автомобіль за цей проміжок часу.
.
Знайти: 1) роботу, що виконується за
перші
руху; 2) середню потужність, що розвиває
автомобіль за цей проміжок часу.
Дві кулі масами
 і
і
 рухаються по гладкій горизонтальній
поверхні назустріч одна одній зі
швидкостями
рухаються по гладкій горизонтальній
поверхні назустріч одна одній зі
швидкостями
 і
і
 відповідно. Чому дорівнює зміна
внутрішньої енергії куль після їх
непружного зіткнення?
відповідно. Чому дорівнює зміна
внутрішньої енергії куль після їх
непружного зіткнення?
Пружина жорсткістю
 була стиснута на
була стиснута на
 .
Яку потрібно виконати роботу, щоб
стиснути пружину на
.
Яку потрібно виконати роботу, щоб
стиснути пружину на
 ?
?
Тіло масою
 летить зі швидкістю
летить зі швидкістю
 і
пружно вдаряється у стінку під кутом
і
пружно вдаряється у стінку під кутом
 до неї. Знайти імпульс сили при ударі.
до неї. Знайти імпульс сили при ударі.
Кран піднімає вантаж масою
 на висоту
на висоту
 за
за
 .
Знайдіть механічну потужність. Силами
тертя знехтувати.
.
Знайдіть механічну потужність. Силами
тертя знехтувати.
Літак має чотири двигуна, сила тяги кожного
 .
Яка корисна потужність двигунів при
польоті літака зі швидкістю
.
Яка корисна потужність двигунів при
польоті літака зі швидкістю
 .
.
На висоті
 від поверхні Землі м’яч мав швидкість
від поверхні Землі м’яч мав швидкість
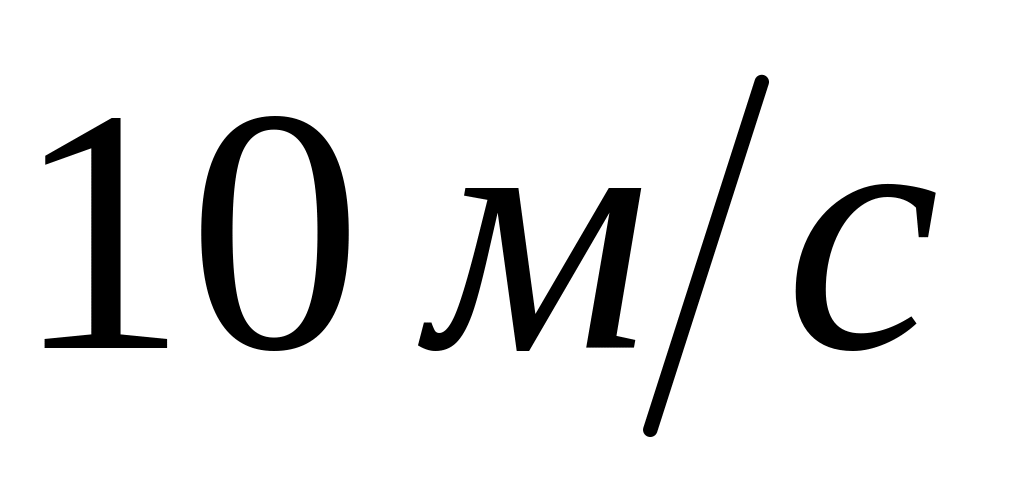 .
З якою швидкістю він буде рухатись
біля поверхні Землі? Опором повітря
знехтувати.
.
З якою швидкістю він буде рухатись
біля поверхні Землі? Опором повітря
знехтувати.
Знайти мінімальне значення гальмівного шляху автомобіля, якщо він почав сповільнювати рух на горизонтальній ділянці шоссе при швидкості руху
 .
Коефіцієнт тертя
.
Коефіцієнт тертя
 .
.
Автомобіль масою розганяється з місця на гору під кутом . Коефіцієнт опору . Автомобіль набуває швидкості
 на ділянці завдовжки
на ділянці завдовжки
 .
Яку середню потужність
.
Яку середню потужність
 розвиває двигун?
розвиває двигун?
Яку роботу потрібно виконати, щоб змусити тіло масою
 ,
яке рухається: 1) збільшити свою швидкість
від
,
яке рухається: 1) збільшити свою швидкість
від
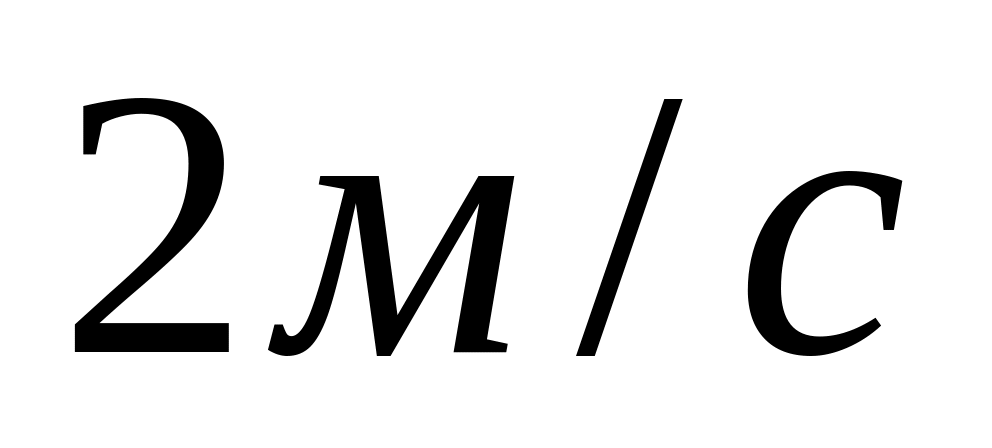 до
до
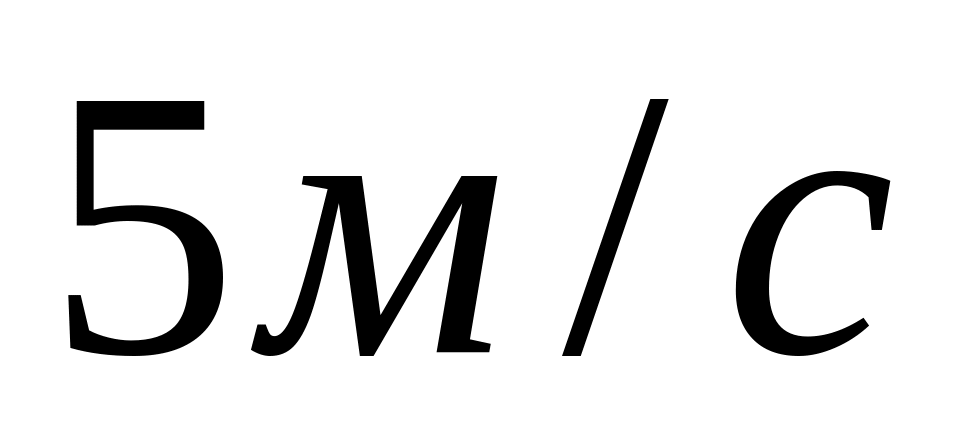 ;
2)
зупинитися при початковій швидкості
в
;
2)
зупинитися при початковій швидкості
в
 ?
?
Вагон вагою в
 ,
який рухається рівноуповільнено, під
дією сили тертя в
,
який рухається рівноуповільнено, під
дією сили тертя в
 через деякий час зупиняється. Початкова
швидкість вагону рівна
через деякий час зупиняється. Початкова
швидкість вагону рівна
 .
Знайти: 1) роботу сил тертя, 2) відстань,
яку вагон пройде до зупинки.
.
Знайти: 1) роботу сил тертя, 2) відстань,
яку вагон пройде до зупинки.
Побудувати графік залежності від часу кінетичної, потенціальної і повної енергії каменя масою в
 ,
кинутого вертикально вгору з початковою
швидкістю
,
кинутого вертикально вгору з початковою
швидкістю
 ,
для
,
для
 через кожні
через кожні
 .
.
З вежі висотою
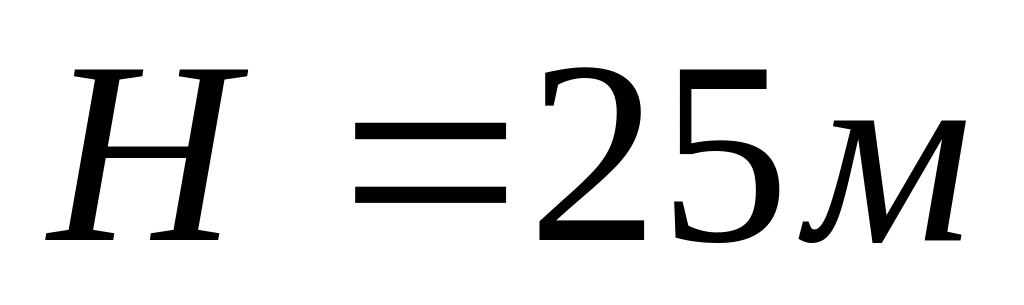 горизонтально кинутий камінь зі
швидкістю
горизонтально кинутий камінь зі
швидкістю
 .
Знайти кінетичну і потенціальну енергію
каменя через одну секунду після початку
руху. Маса каменя
.
Знайти кінетичну і потенціальну енергію
каменя через одну секунду після початку
руху. Маса каменя
 .
Опором повітря знехтувати.
.
Опором повітря знехтувати.
Матеріальна точка масою
 рухається по колу радіусом в
рухається по колу радіусом в
 з постійним тангенціальним прискоренням.
Знайти величину тангенціального
прискорення, якщо відомо, що до кінця
другого оберту після початку руху
кінетична енергія матеріальної точки
стала рівною
з постійним тангенціальним прискоренням.
Знайти величину тангенціального
прискорення, якщо відомо, що до кінця
другого оберту після початку руху
кінетична енергія матеріальної точки
стала рівною

З похилої площини висотою
 і довжиною схилу
і довжиною схилу
 ковзає тіло масою в
.
Знайти: 1) кінетичну енергію тіла біля
основи площини; 2) швидкість тіла біля
основи площини; 3) відстань, пройдену
тілом по горизонтальній частині шляху
до зупинки. Коефіцієнт тертя на всьому
шляху вважати постійним і рівним
.
ковзає тіло масою в
.
Знайти: 1) кінетичну енергію тіла біля
основи площини; 2) швидкість тіла біля
основи площини; 3) відстань, пройдену
тілом по горизонтальній частині шляху
до зупинки. Коефіцієнт тертя на всьому
шляху вважати постійним і рівним
.
Людина масою
 ,
яка біжить зі швидкістю
,
яка біжить зі швидкістю
 доганяє візок масою
доганяє візок масою
 ,
що рухається зі швидкістю
,
що рухається зі швидкістю
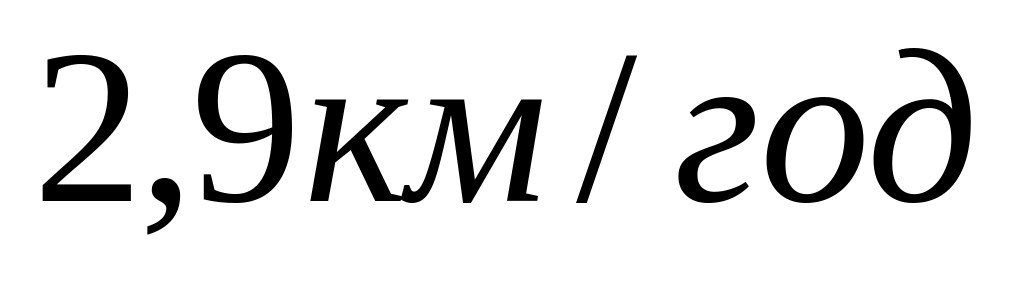 ,
і вистрибує на нього. Знайти з якою
швидкістю стане рухатись візок? З якою
швидкістю рухався б візок, якби людина
бігла йому назустріч?
,
і вистрибує на нього. Знайти з якою
швидкістю стане рухатись візок? З якою
швидкістю рухався б візок, якби людина
бігла йому назустріч?
Граната, що летіла зі швидкістю
 ,
вибухнула і розірвалася на дві частини.
Велика частина, вага якої складала з
,
вибухнула і розірвалася на дві частини.
Велика частина, вага якої складала з
 ваги всієї гранати, продовжувала
рухатися в попередньому напрямку, але
із збільшеною швидкістю, рівною
ваги всієї гранати, продовжувала
рухатися в попередньому напрямку, але
із збільшеною швидкістю, рівною
 .
Знайти швидкість меншої частини.
.
Знайти швидкість меншої частини.
Із гармати масою
 вилітає снаряд вагою
вилітає снаряд вагою
 .
Кінетична енергія при вильоті снаряду
рівна
.
Кінетична енергія при вильоті снаряду
рівна
 .
Яку кінетичну енергію отримує гармата
внаслідок віддачі.
.
Яку кінетичну енергію отримує гармата
внаслідок віддачі.
Два тіла рухаються на зустріч один одному і ударяються не пружно. Швидкість першого тіла до удару рівна
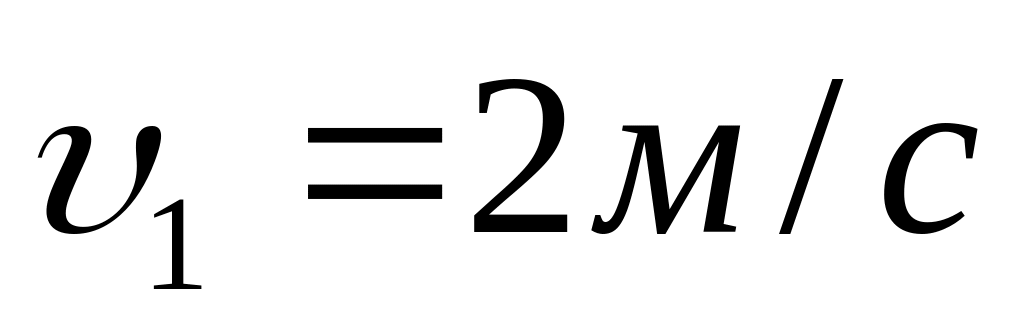 ,
швидкість другого
,
швидкість другого
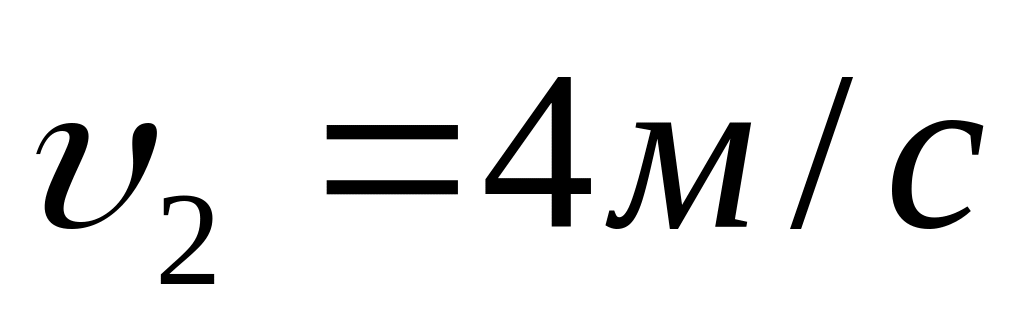 .
Загальна швидкість після удару по
напрямку співпадає з напрямком швидкості
і рівна
.
Загальна швидкість після удару по
напрямку співпадає з напрямком швидкості
і рівна
 .
У скільки разів кінетична енергія
першого тіла була більша кінетичної
енергії другого тіла?
.
У скільки разів кінетична енергія
першого тіла була більша кінетичної
енергії другого тіла?
Куля, що летить горизонтально, потрапляє у вантаж, підвішений на дуже легкому жорсткому стержні, і застряє в ньому. Маса кулі в
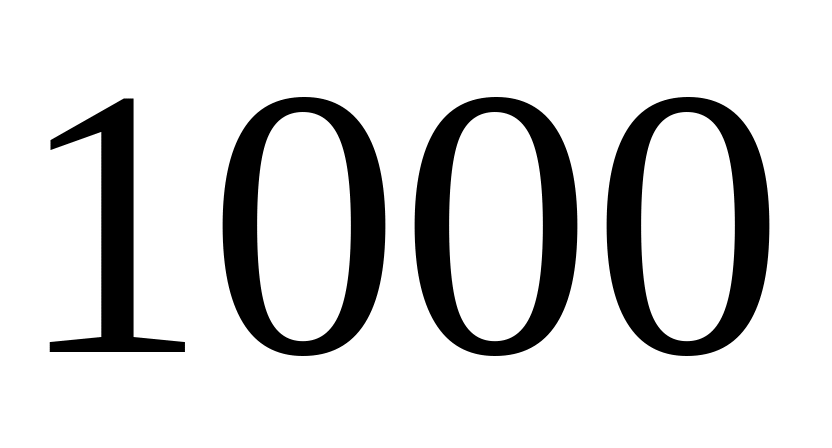 разів менша маси вантажу. Відстань від
точки підвісу стержня до центру вантажу
рівна
.
Знайти швидкість кулі, якщо відомо, що
стержень з вантажем відхилився від
удару кулі на кут
разів менша маси вантажу. Відстань від
точки підвісу стержня до центру вантажу
рівна
.
Знайти швидкість кулі, якщо відомо, що
стержень з вантажем відхилився від
удару кулі на кут
 .
.
Дерев’яна куля падає вертикально вниз з висоти без початкової швидкості. Коефіцієнт відновлення при ударі кулі об підлогу вважати рівним . Знайти : 1) висоту, на яку підніметься куля після удару об підлогу, 2) кількість тепла, яка виділиться при цьому ударі. Маса кулі
 .
.
Крижина площею поперечного перерізу
 і висотою
і висотою
 плаває у воді. Яку роботу треба здійснити,
щоб повністю занурити крижину у воду?
плаває у воді. Яку роботу треба здійснити,
щоб повністю занурити крижину у воду?
Хлопчик, стріляючи з рогатки, натягнув гумовий шнур так, що його довжина стала більша на
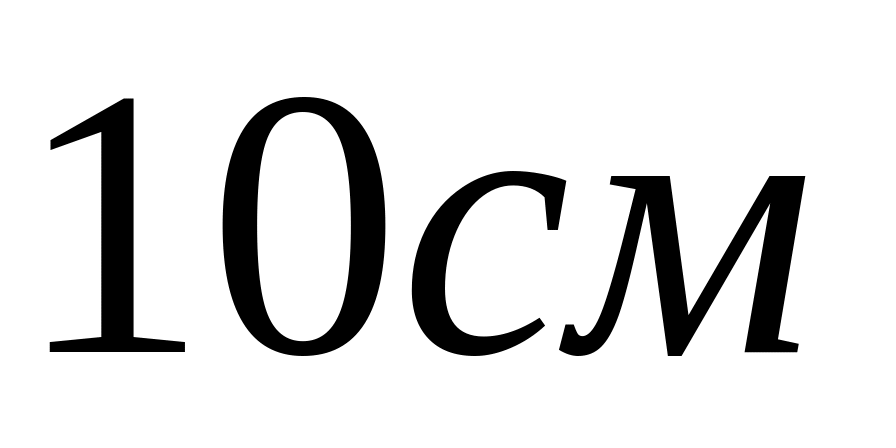 .
З
якою швидкістю полетів камінь масою
.
З
якою швидкістю полетів камінь масою
 ?
Для натягу гумового шнура на
?
Для натягу гумового шнура на
 потрібна сила в
.
Опором повітрі при польоті каменя
знехтувати.
потрібна сила в
.
Опором повітрі при польоті каменя
знехтувати.
Яку роботу виконують двигуни електропотяга на шляху при розгоні с прискоренням
 вгору по площині з кутом нахилу
,
якщо маса електропотяга
вгору по площині з кутом нахилу
,
якщо маса електропотяга
 ,
а коефіцієнт тертя
?
,
а коефіцієнт тертя
?
Визначити потужність двигуна шахтної клітки, який піднімає із шахти глибиною
 вантаж масою
вантаж масою
 за
за
 ,
якщо ККД рівний
,
якщо ККД рівний
 .
.
Якою кінетичною енергією володіло тіло масою , якщо воно піднялося по похилій площині з кутом нахилу
 на висоту
?
Коефіцієнт тертя між тілом і похилою
площиною
на висоту
?
Коефіцієнт тертя між тілом і похилою
площиною
 .
.
Яка енергій пішла на деформацію двох куль, які зіткнулися, масами
 ,
якщо вони рухались на зустріч одна
одній зі швидкостями
,
якщо вони рухались на зустріч одна
одній зі швидкостями
 і
і
 ,
а удар був прямий і не пружний?
,
а удар був прямий і не пружний?
Із гармати масою
 зроблений постріл в горизонтальному
напрямку. Маса снаряду
зроблений постріл в горизонтальному
напрямку. Маса снаряду
 .
Швидкість снаряду відносно Землі
.
Швидкість снаряду відносно Землі
 .
Визначити швидкість вільного відкоту
знаряддя в момент вильоту снаряда.
.
Визначити швидкість вільного відкоту
знаряддя в момент вильоту снаряда.
Два човни масою
 кожний ідуть паралельним курсом
назустріч один одному з однаковою
швидкістю
.
Коли човни зустрічаються, із першого
в другий перекидають вантаж
кожний ідуть паралельним курсом
назустріч один одному з однаковою
швидкістю
.
Коли човни зустрічаються, із першого
в другий перекидають вантаж
 ,
а потім із другого човна в перший
перекидають такий же вантаж. В інший
раз вантажі перекидають із човна в
човен одночасно. Визначити швидкості
човнів в обох випадках.
,
а потім із другого човна в перший
перекидають такий же вантаж. В інший
раз вантажі перекидають із човна в
човен одночасно. Визначити швидкості
човнів в обох випадках.
Визначити масу тіла, яке здійснює гармонічне коливання з амплітудою
 ,
частотою
,
частотою
 і початковою фазою
,якщо
повна енергія коливання
і початковою фазою
,якщо
повна енергія коливання
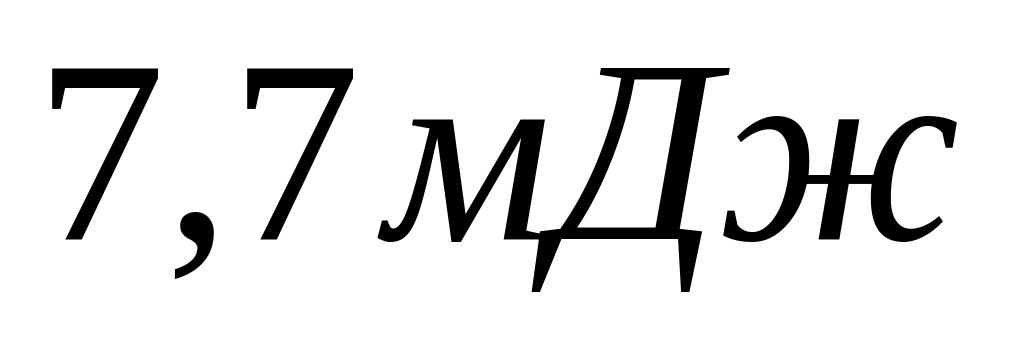 .
Через скільки секунд від початку відліку
часу кінетична енергія буде рівна
потенціальній?
.
Через скільки секунд від початку відліку
часу кінетична енергія буде рівна
потенціальній?
Тіло масою
 здійснює коливання, яке описується
рівнянням:
здійснює коливання, яке описується
рівнянням:
 .
.Знайти значення кінетичної і потенціальної енергії тіла через
 від моменту часу
від моменту часу
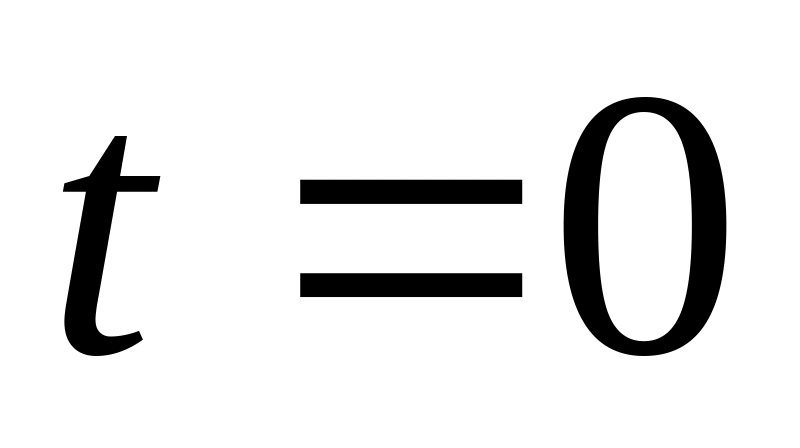 .Чому
рівна повна енергія тіла?
.Чому
рівна повна енергія тіла?
Визначити амплітуду гармонічних коливань матеріальної точки, якщо її повна коливальна енергія
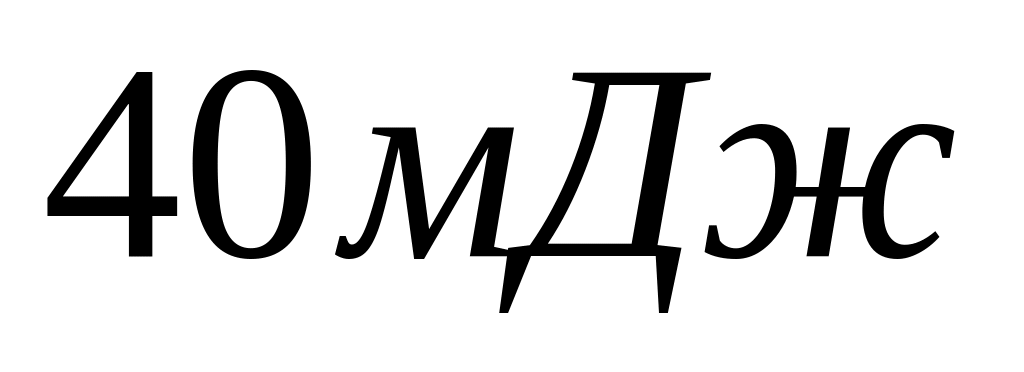 ,
а діюча на неї сила при зміщенні, рівному
половині амплітуди,
,
а діюча на неї сила при зміщенні, рівному
половині амплітуди,
 .
.
В скільки раз зменшиться повна енергія коливань секундного маятника за
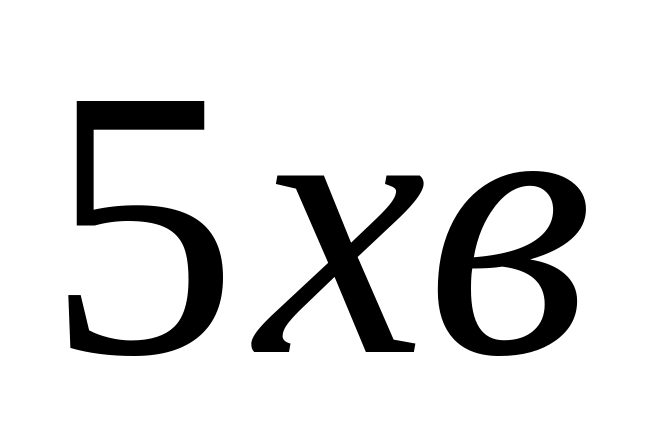 ,
якщо логарифмічний декремент згасання
,
якщо логарифмічний декремент згасання
 ?
?
Амплітуда коливання камертона за
 зменшилася в
зменшилася в
 раз.
Знайти коефіцієнт затухання коливань.
раз.
Знайти коефіцієнт затухання коливань.
Як зміниться хід маятникового годинника при підняті їх на висоту
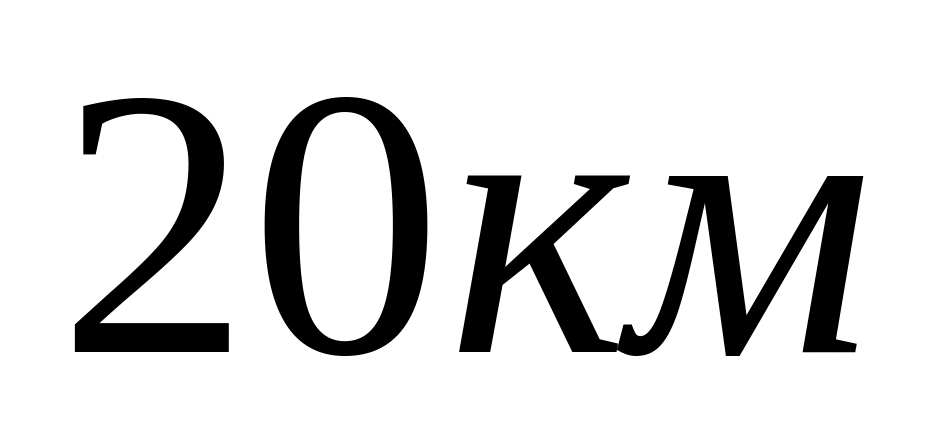 над поверхнею Землі?
над поверхнею Землі?
Визначити амплітуду вимушених коливань вантажу масою , підвішеного на пружині жорсткістю
 ,
якщо діє вимушена сила з амплітудою
і частотою в
,
якщо діє вимушена сила з амплітудою
і частотою в
 рази більшою власної частоти коливання
вантажу, а коефіцієнт затухання
рази більшою власної частоти коливання
вантажу, а коефіцієнт затухання
 .
.
Дві кулі масами
 і
і
 ,
скріплені між собою пружиною, жорсткість
якої
,
лежать на горизонтальній площинні.
Пружина розтягується і відпускається.
Визначити період коливань, які виникнули.
Тертям знехтувати.
,
скріплені між собою пружиною, жорсткість
якої
,
лежать на горизонтальній площинні.
Пружина розтягується і відпускається.
Визначити період коливань, які виникнули.
Тертям знехтувати.
На якій відстані від джерела коливань, які здійснюються по закону синуса, в момент часу
 зміщення точки від положення рівноваги
рівне половині амплітуди? Швидкість
розповсюдження коливань
зміщення точки від положення рівноваги
рівне половині амплітуди? Швидкість
розповсюдження коливань
 .
Період коливань
.
Період коливань
 .
.
В скільки раз змінюється довжина ультразвукової хвилі при переході хвилі із сталі в мідь, якщо швидкість розповсюдження ультразвуку в міді і сталі відповідно
 і
і
 ?
?
Знайти швидкість розповсюдження ультразвуку в залізі, якщо модуль Юнга для заліза
 ,
а густина
,
а густина
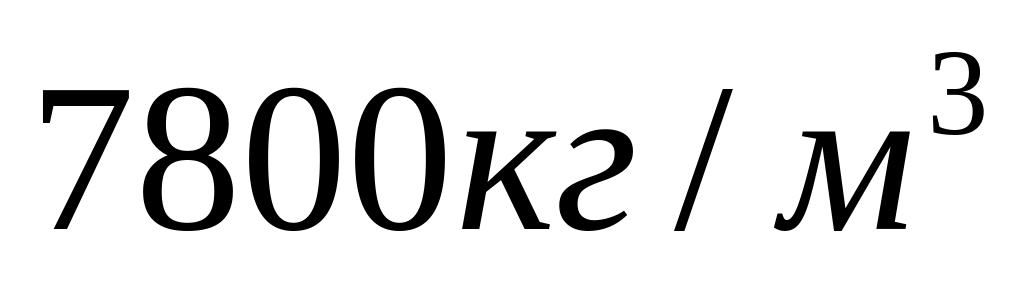 .
.
Чому рівна швидкість розповсюдження звукової хвилі в мідній дротині довжиною , яка натягнута силою
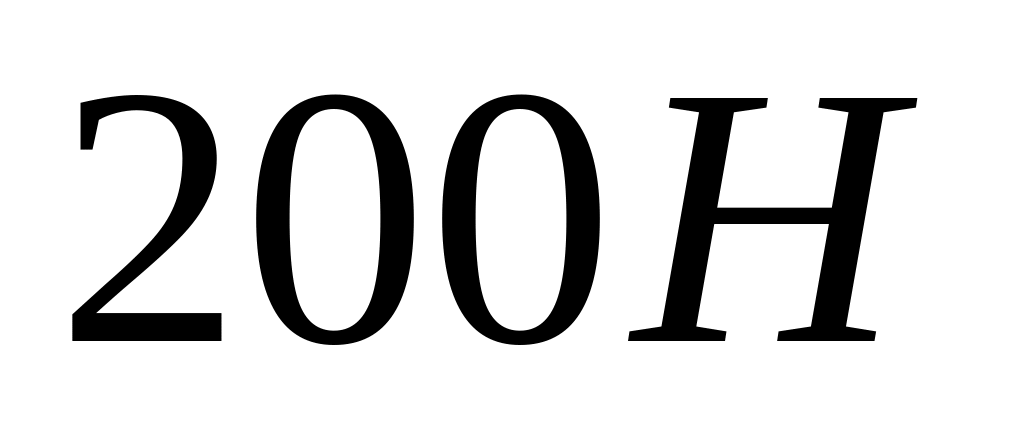 ?
Маса дротини
?
Маса дротини
 .
.
Рівень гучності шуму літака на відстані
 рівний
рівний

 ,
а тихої розмови на тій же відстані –
,
а тихої розмови на тій же відстані –
 .
Визначити відношення інтенсивностей
і абсолютні значення інтенсивностей
цих звуків.
.
Визначити відношення інтенсивностей
і абсолютні значення інтенсивностей
цих звуків.
Підводний човен, який рухається зі швидкістю
 ,
посилає ультразвуковий сигнал частотою
,
посилає ультразвуковий сигнал частотою
 ,
який відбившись від перешкод, повертається
назад. Визначити різницю між частотами
посланого і прийнятого сигналів.
,
який відбившись від перешкод, повертається
назад. Визначити різницю між частотами
посланого і прийнятого сигналів.
Два електропоїзди йдуть назустріч один одному зі швидкостями
 і
і
 .
Перший поїзд дає свисток, висота тону
якого відповідає частоті
.
Перший поїзд дає свисток, висота тону
якого відповідає частоті
 Визначити частоту, яка сприймається
пасажиром другого електропоїзду перед
зустріччю і після зустрічі поїздів.
Чому були б рівні відповідні частоти,
якби пасажир знаходився у першому
електропоїзді, а сигнал давав другий?
Визначити частоту, яка сприймається
пасажиром другого електропоїзду перед
зустріччю і після зустрічі поїздів.
Чому були б рівні відповідні частоти,
якби пасажир знаходився у першому
електропоїзді, а сигнал давав другий?
Амплітуда гармонічних коливань точки
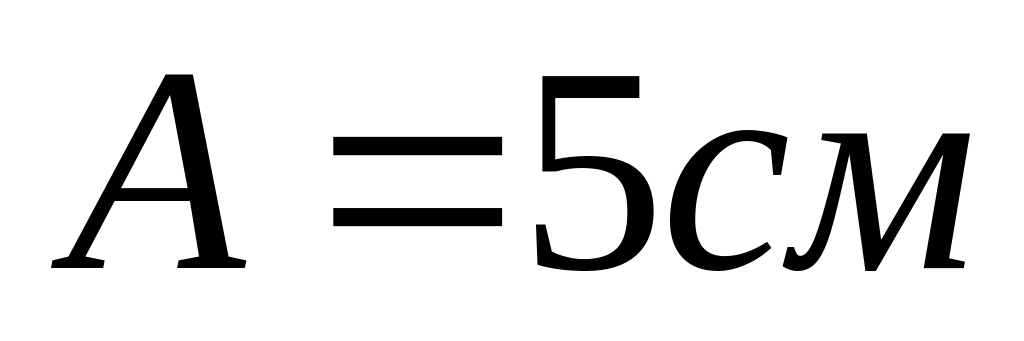 ,
амплітуда швидкості
,
амплітуда швидкості
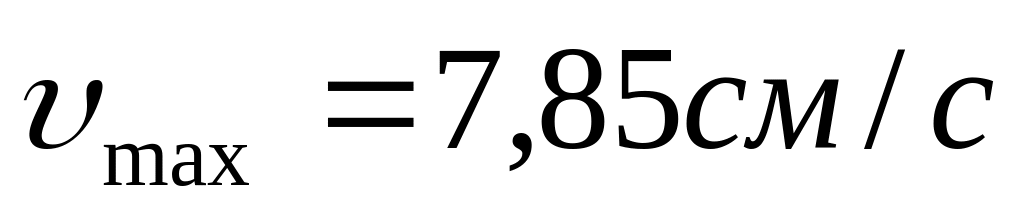 .
Обчислити циклічну частоту
коливань і максимальне прискорення
.
Обчислити циклічну частоту
коливань і максимальне прискорення
 точки.
точки.
Точка здійснює коливання за законом синуса з періодом
 .
У деякий момент часу зміщення
точки дорівнювало
.
Коли фаза коливань збільшилась удвічі,
швидкість
точки стала дорівнювати
.
У деякий момент часу зміщення
точки дорівнювало
.
Коли фаза коливань збільшилась удвічі,
швидкість
точки стала дорівнювати

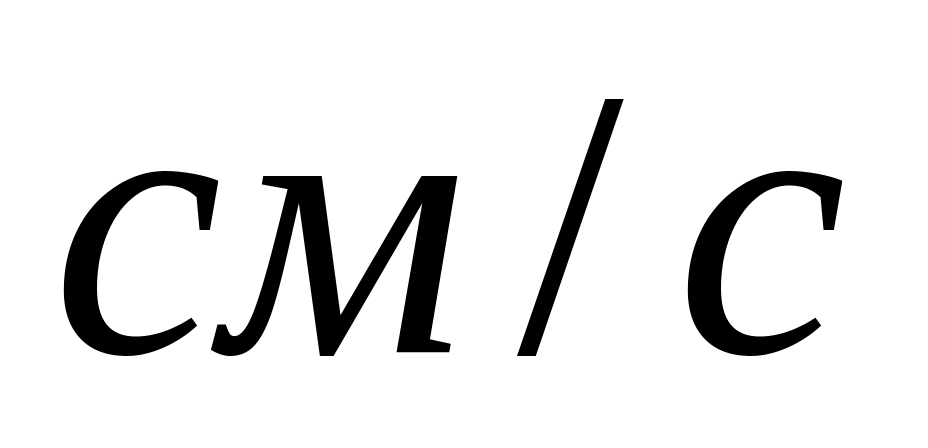 .
Визначити амплітуду
.
Визначити амплітуду
 коливань.
коливань.
Точка бере участь одночасно у двох коливаннях однакового напряму, які відбуваються за законами
 і
і
 .
Визначити швидкість
і прискорення
точки через час
.
Визначити швидкість
і прискорення
точки через час
 після початку коливань, а також
максимальну швидкість
після початку коливань, а також
максимальну швидкість
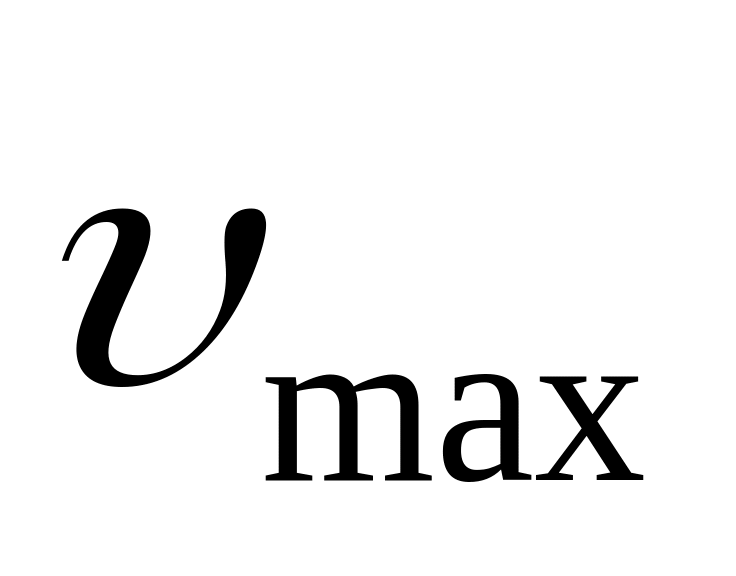 точки.
точки.
Матеріальна точка, маса якої , здійснює гармонічні коливання за законом косинуса з періодом
 і початковою фазою
і початковою фазою
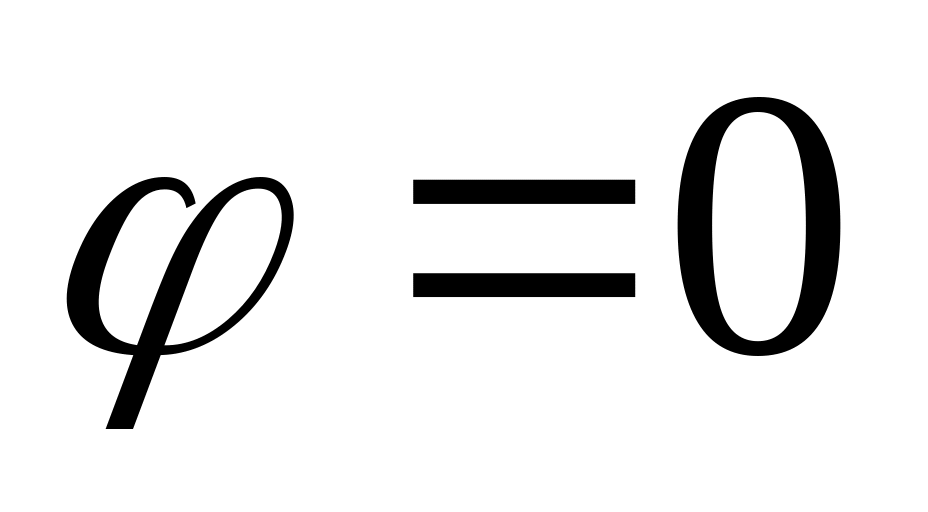 .
Повна механічна енергія точки
.
Повна механічна енергія точки
 .
Визначити амплітуду коливань
і записати закон руху точки. Обчислити
максимальне значення
.
Визначити амплітуду коливань
і записати закон руху точки. Обчислити
максимальне значення
 сили, що діє на точку.
сили, що діє на точку.
Матеріальна точка, маса якої , здійснює гармонічні коливання. Амплітуда коливань
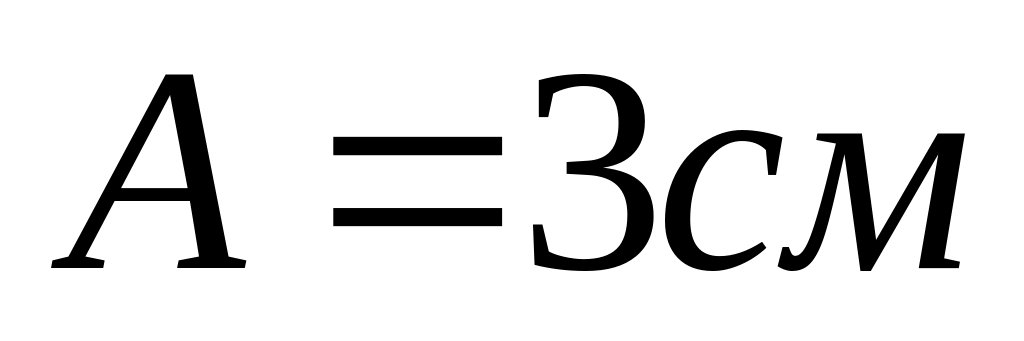 ,
частота
,
частота
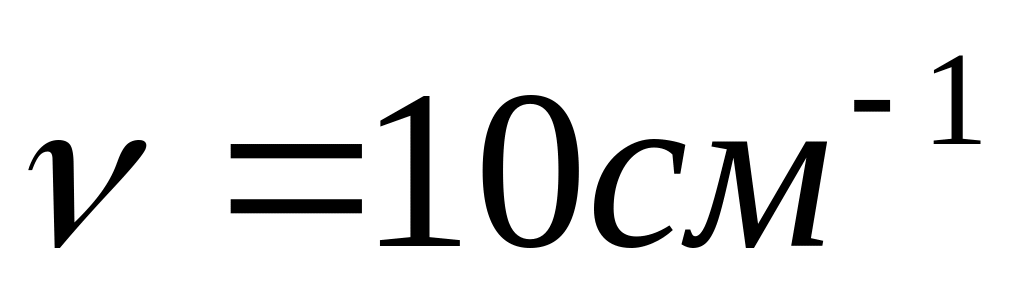 ,
початкова фаза
.
Встановити закон, за яким змінюється
сила
,
що діє на точку. Визначити повну механічну
енергію
точки, значення діючої сили
та відношення потенціальної енергії
до кінетичної
,
початкова фаза
.
Встановити закон, за яким змінюється
сила
,
що діє на точку. Визначити повну механічну
енергію
точки, значення діючої сили
та відношення потенціальної енергії
до кінетичної
 для моменту часу, коли точка відхилена
від положення рівноваги на
для моменту часу, коли точка відхилена
від положення рівноваги на
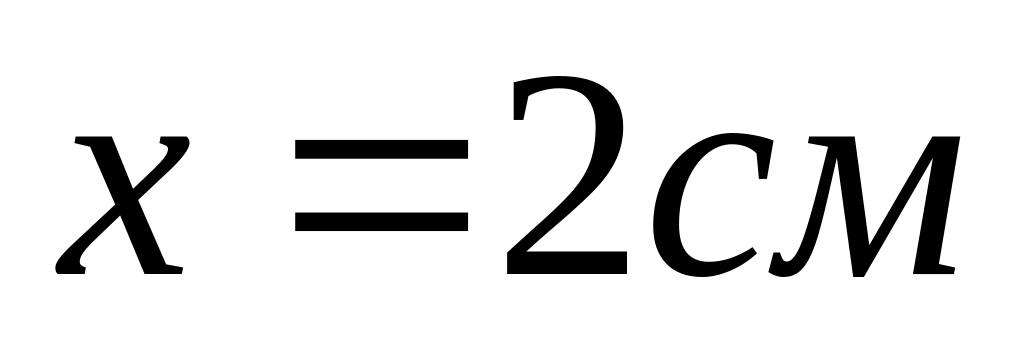 .
.
Кулька підвішена на нитці завдовжки . Її відхиляють на кут
 і спостерігають коливання. Визначити
швидкість кульки під час проходження
нею положення рівноваги, вважаючи
коливання незгасаючими гармонічними.
Перевірити розв’язок, обчисливши
швидкість кульки з рівнянь механіки.
і спостерігають коливання. Визначити
швидкість кульки під час проходження
нею положення рівноваги, вважаючи
коливання незгасаючими гармонічними.
Перевірити розв’язок, обчисливши
швидкість кульки з рівнянь механіки.
Брусок, маса якого
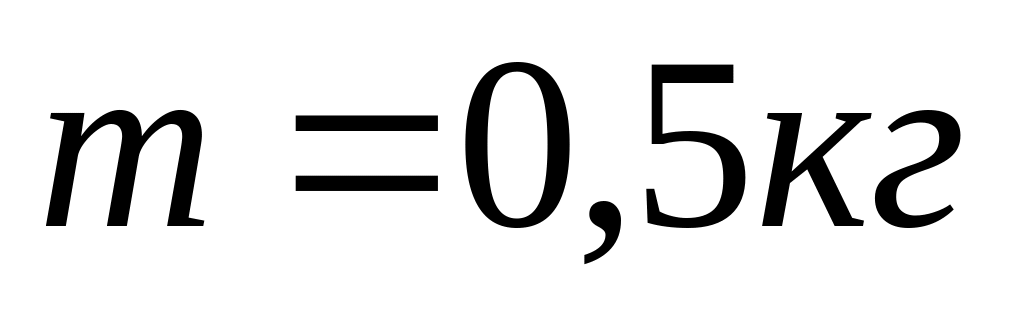 ,
лежить на гладкому столі. Його з’єднано
горизонтально пружиною жорсткістю
,
лежить на гладкому столі. Його з’єднано
горизонтально пружиною жорсткістю
 зі стіною. У початковий момент часу
пружину стиснули на
зі стіною. У початковий момент часу
пружину стиснули на
 і відпустили. Встановити закон руху
бруска. Тертям нехтувати.
і відпустили. Встановити закон руху
бруска. Тертям нехтувати.
Тягарець масою , підвішений на спіральній пружині, розтягує її на
 .
Яку амплітуду
матимуть коливання тягарця, якщо повна
механічна енергія
.
Яку амплітуду
матимуть коливання тягарця, якщо повна
механічна енергія
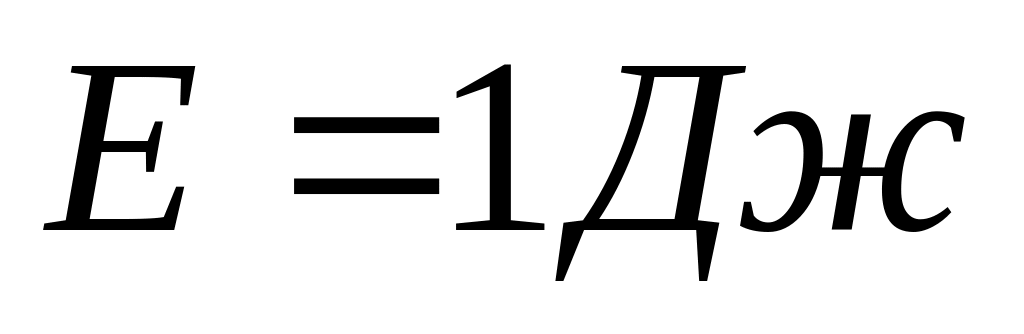 ?
?
Точка, здійснює коливання за законом
 ,
де
–
зміщення,
,
де
–
зміщення,
 .
У деякий момент часу прискорення
становило
.
У деякий момент часу прискорення
становило
 .
Визначити модуль швидкості
.
Визначити модуль швидкості
 точки в цей момент часу.
точки в цей момент часу.
Матеріальна точка, маса якої , здійснює коливання за законом
 ,
де
–
зміщення,
;
,
де
–
зміщення,
;
 –
аргумент синуса,
–
аргумент синуса,
 .
Визначити максимальні значення сили
,
що повертає точку в положення рівноваги,
і кінетичної енергії
.
Визначити максимальні значення сили
,
що повертає точку в положення рівноваги,
і кінетичної енергії
 .
.
Написати рівняння гармонічного коливального руху з амплітудою
 ,
якщо за
,
якщо за
 здійснюється
здійснюється
 коливань і початкова фаза коливань
рівна
коливань і початкова фаза коливань
рівна
 .
Накреслити графік цього руху.
.
Накреслити графік цього руху.
Амплітуда гармонічних коливань рівна
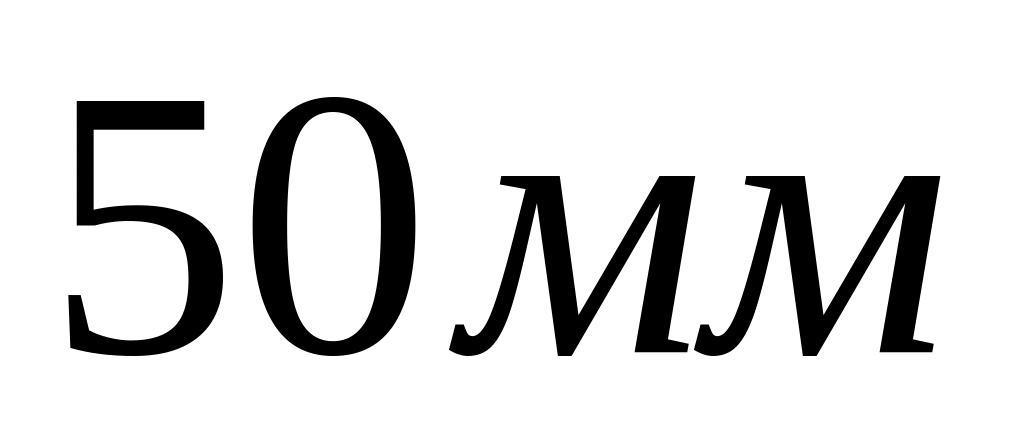 ,
період
,
період
 і початкова фаза
і початкова фаза
 .
1) Написати рівняння цього коливання.
2) Знайти зміщення точки, яка коливається
від положення рівноваги при
і при
.
1) Написати рівняння цього коливання.
2) Знайти зміщення точки, яка коливається
від положення рівноваги при
і при
 .
3) Накреслити графік цього руху.
.
3) Накреслити графік цього руху.
Накреслити на одному графіку два гармонічних коливання з однаковими амплітудами
 і однаковими періодами
і однаковими періодами
 ,
але які мають різницю фаз:
.
,
але які мають різницю фаз:
.
Через який час від початку руху точка, яка здійснює коливальний рух за рівнянням
 ,
проходить шлях від положення рівноваги
до максимального зміщення?
,
проходить шлях від положення рівноваги
до максимального зміщення?
Амплітуда гармонічного коливання рівна , період . Знайти максимальну швидкість точки, яка коливається, і її максимальне прискорення.
Точка здійснює гармонічне коливання. Період коливання , амплітуда , початкова фаза рівна нулю. Знайти швидкість точки в момент часу, коли зміщення точки від положення рівноваги рівне
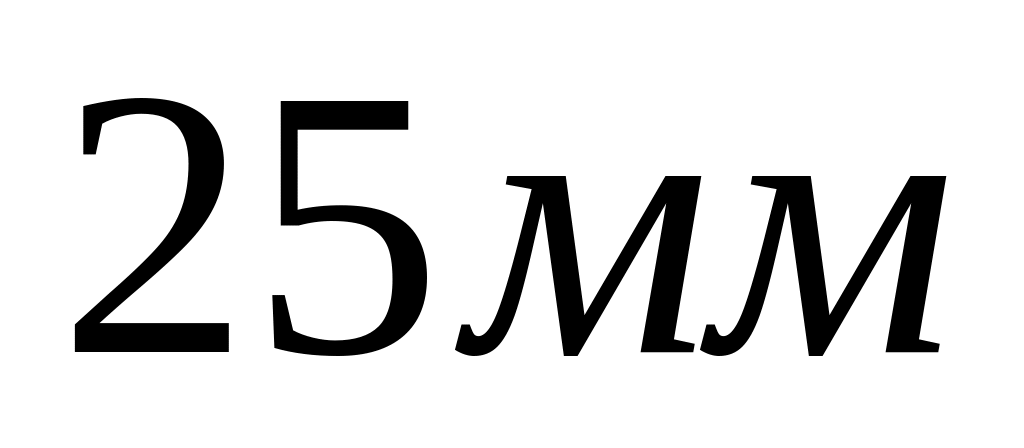 .
.
Амплітуда гармонічних коливань матеріальної точки
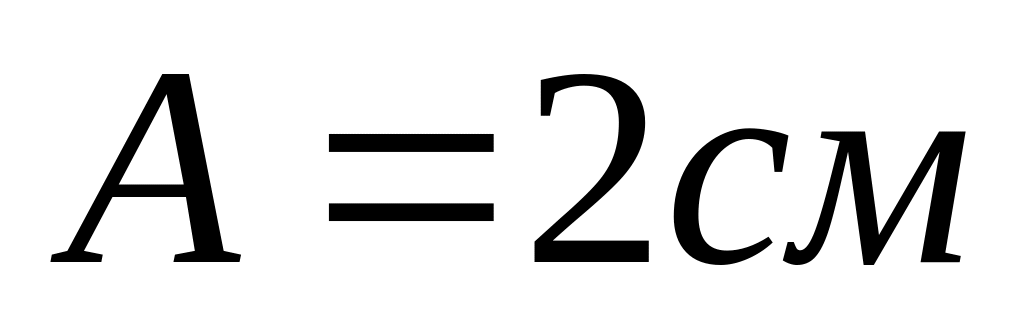 ,
повна енергія коливань
,
повна енергія коливань
 .
При якому зміщення від положення
рівноваги на точку, яка коливається,
діє сила
.
При якому зміщення від положення
рівноваги на точку, яка коливається,
діє сила
 ?
?
До пружини підвішений вантаж
 .
Знаючи, що пружина під дією сили в
розтягується на
.
Знаючи, що пружина під дією сили в
розтягується на
 ,
визначити період вертикальних коливань
вантажу.
,
визначити період вертикальних коливань
вантажу.
Ареометр вагою
 плаває в рідині. Якщо занурити його
трохи в рідину і відпустити, то він
почне здійснювати коливання з періодом
плаває в рідині. Якщо занурити його
трохи в рідину і відпустити, то він
почне здійснювати коливання з періодом
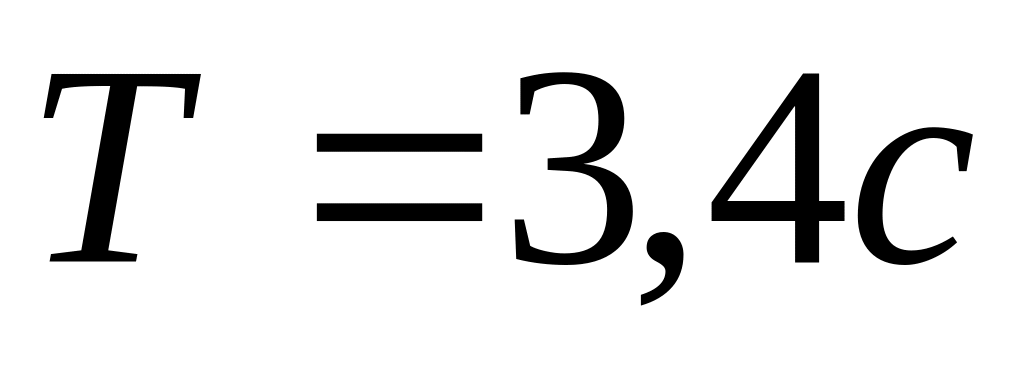 .
Вважаючи коливання незатухаючими,
знайти за результатами досліду густину
рідини
,
в якій плаває ареометр. Діаметр
вертикальної циліндричної труби
ареометра рівний
.
Вважаючи коливання незатухаючими,
знайти за результатами досліду густину
рідини
,
в якій плаває ареометр. Діаметр
вертикальної циліндричної труби
ареометра рівний
 .
.
Логарифмічний декремент затухання математичного маятника рівний
 .
Знайти, в скільки разів зменшиться
амплітуда коливань за одне повне
коливання маятника.
.
Знайти, в скільки разів зменшиться
амплітуда коливань за одне повне
коливання маятника.
Математичний маятник здійснює затухаючі коливання з логарифмічним декрементом затухання, рівним . У скільки разів зменшиться повне прискорення маятника в його крайньому положенні за одне коливання?
Період затухаючих коливань , логарифмічний декремент затухання
 ,
початкова фаза рівна нулю. Зміщення
точки при
,
початкова фаза рівна нулю. Зміщення
точки при
 рівне
рівне
 .
Записати рівняння усього коливного
процесу та побудувати його графік у
межах двох періодів.
.
Записати рівняння усього коливного
процесу та побудувати його графік у
межах двох періодів.
Рівняння незатухаючих коливань дано у вигляді
 .
Знайти зміщення від положення рівноваги,
швидкість і прискорення точки, яка
знаходиться на відстані
.
Знайти зміщення від положення рівноваги,
швидкість і прискорення точки, яка
знаходиться на відстані
 від
джерела коливань, для моменту
після початку коливань. Швидкість
розповсюдження коливань рівна
від
джерела коливань, для моменту
після початку коливань. Швидкість
розповсюдження коливань рівна
 .
.
Два поїзди їдуть назустріч один одному зі швидкостями і . Перший поїзд дає сигнал з частотою
 .
Знайти частоту коливань звуку, який
чує пасажир другого поїзду: 1) перед
зустріччю поїздів; 2) після зустрічі
поїздів. Швидкість звуку прийняти
.
Знайти частоту коливань звуку, який
чує пасажир другого поїзду: 1) перед
зустріччю поїздів; 2) після зустрічі
поїздів. Швидкість звуку прийняти
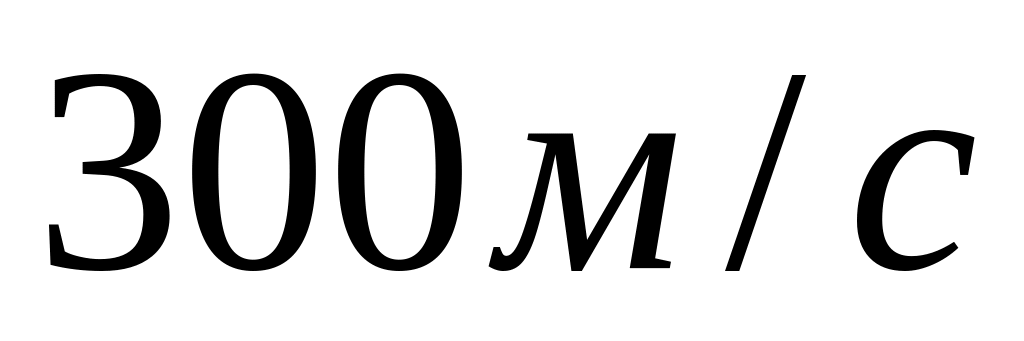 .
.
Визначити глибину, на яку необхідно занурити у воду повітряний пістолет калібру
 ,
щоб при натиску на спусковий гачок
вистріл не здійснився. Довжини стволу
пістолета
,
щоб при натиску на спусковий гачок
вистріл не здійснився. Довжини стволу
пістолета
 .
Маса кулі
.
Маса кулі
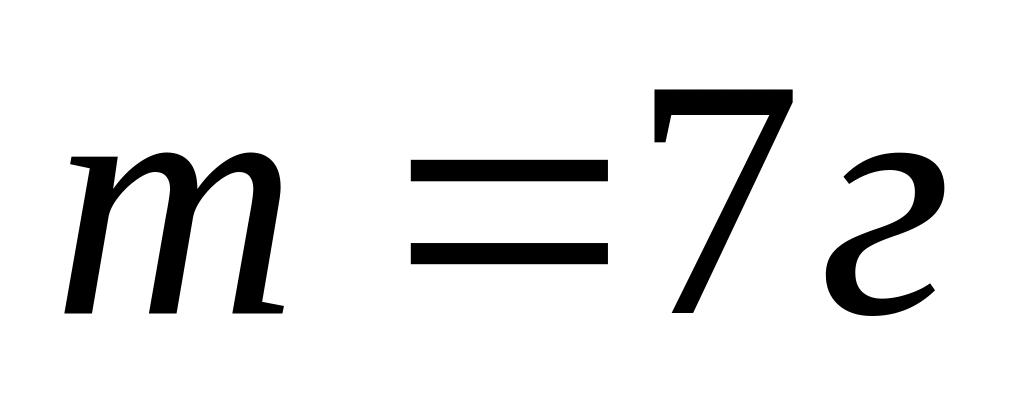 ,
а її швидкість в момент вильоту із
стволу при вистрілі в повітрі
,
а її швидкість в момент вильоту із
стволу при вистрілі в повітрі
 .
.
Визначити натяг тросу при підняті із води залізобетонної плити об’ємом
 з прискоренням
з прискоренням
 .
Лобовим опором знехтувати. Вважати
густину залізобетону
.
Лобовим опором знехтувати. Вважати
густину залізобетону
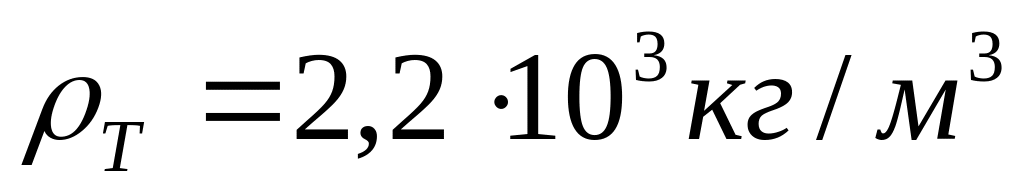 .
.
Дві кулі – алюмінієва і мідна, одна з яких суцільна, а інша порожниста, підвішені до кінців не рівноплечого важеля і врівноважені в повітрі. Встановити, яка із цих куль суцільна, якщо при зануренні їх в посудину з водою рівновага не порушується. Чому рівний об’єм порожнини, якщо маса мідної кулі
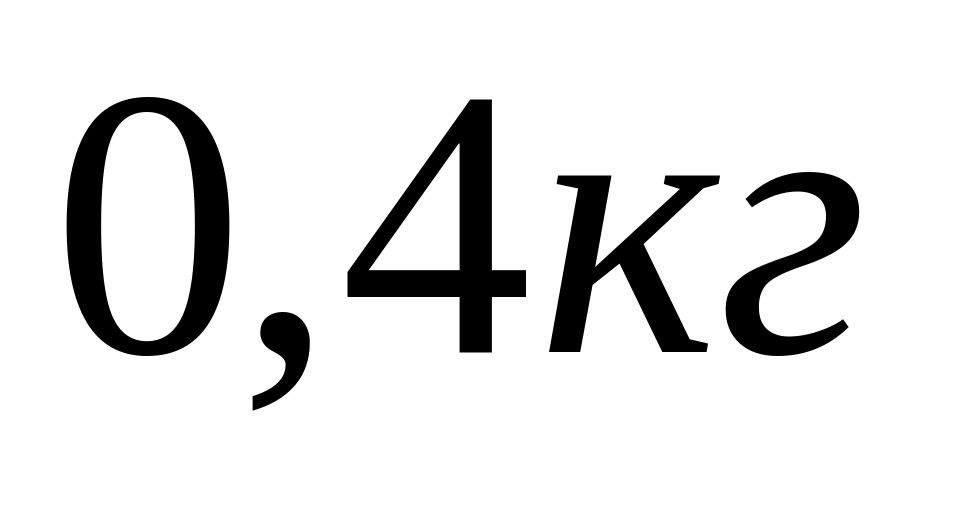 .
.
У посудину зі ртуттю і водою кинута стальна куля. Яка частина об’єму кулі буде знаходитися у воді?
Визначити масу коркового пояса, який здатний втримати людину масою
 у воді так, щоб голова і плечі (
у воді так, щоб голова і плечі (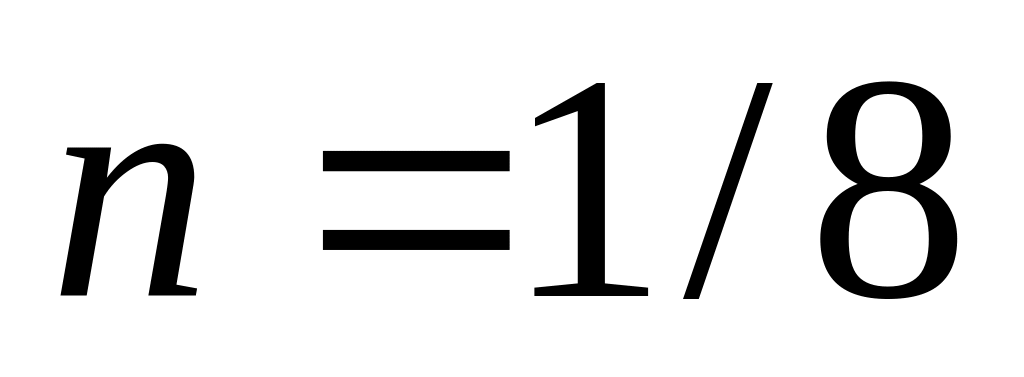 об’єму) не були зануренні у воду. Густину
тіла людини прийняти рівною
об’єму) не були зануренні у воду. Густину
тіла людини прийняти рівною
 .
.
Посудина з водою рухається вертикально з прискоренням
 ,
направленим вгору. Визначити тиск на
глибині
,
направленим вгору. Визначити тиск на
глибині
 .
.
До плаваючого у воді коркового поясу об’ємом
 підвішена на нитці залізна гиря.
Визначити масу гирі і натяг нитки, якщо
у воду занурена
підвішена на нитці залізна гиря.
Визначити масу гирі і натяг нитки, якщо
у воду занурена
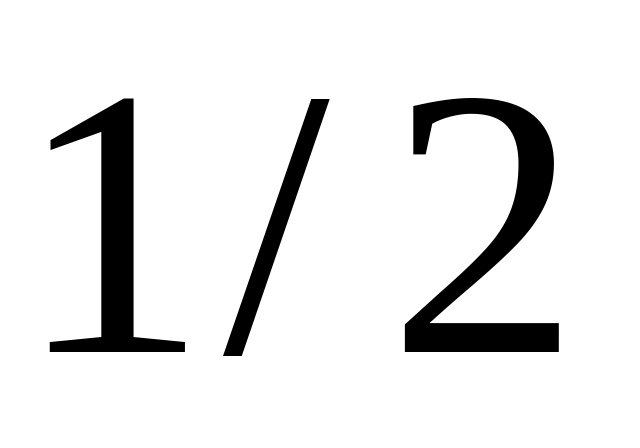 об’єму
пояса.
об’єму
пояса.
По трубі перетином
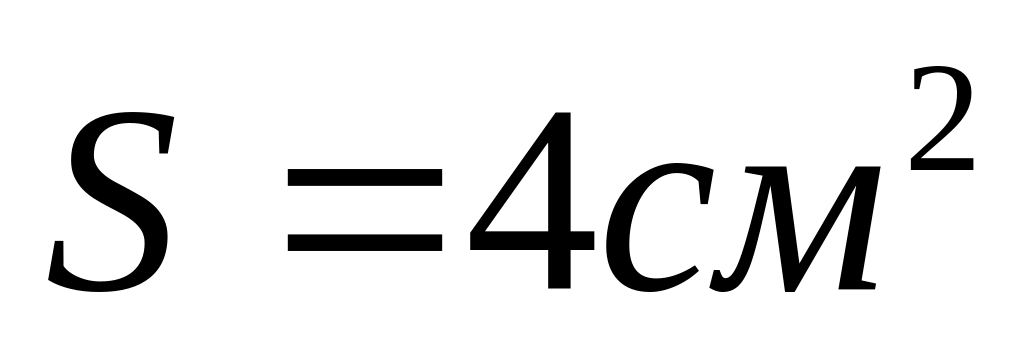 ,
зігнутій під прямим кутом, тече вода.
З якою силою вода діє на трубу, якщо
щосекундна витрата води
,
зігнутій під прямим кутом, тече вода.
З якою силою вода діє на трубу, якщо
щосекундна витрата води
 ?
?
Який опір чинить повітряний потік, який набігає на автомобіль при швидкості руху
 ,
якщо площа лобової поверхні
,
якщо площа лобової поверхні
 ?
Коефіцієнт лобового опору прийняти
рівним
?
Коефіцієнт лобового опору прийняти
рівним
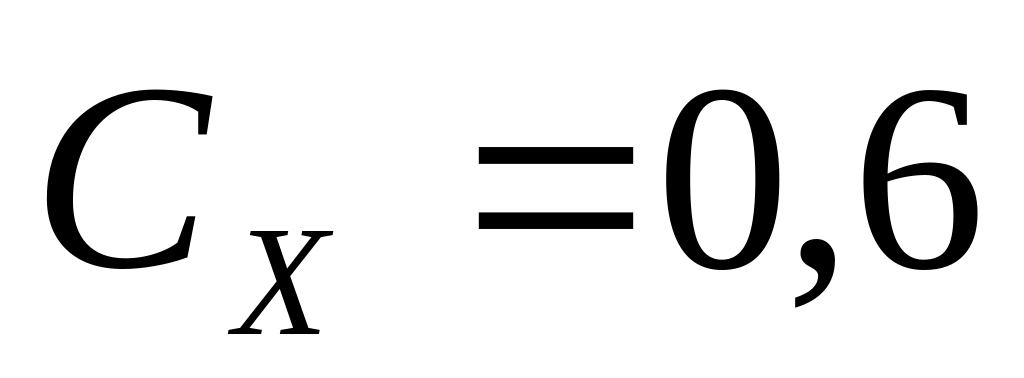 .
.
Визначити потужність повітряного потоку, який набігає на електропоїзд, який рухається зі швидкістю
 ,
якщо площа лобової поверхні
,
якщо площа лобової поверхні
 .
.
Яку потужність розвиває серце людини, якщо при кожному ударі лівий шлуночок, скорочуючись, виштовхує в аорту кров масою
 під тиском
під тиском
 ,
а за
відбувається приблизно
,
а за
відбувається приблизно
 скорочень шлуночка?
скорочень шлуночка?
Визначити роботу, яка виконується при переміщені води об’ємом
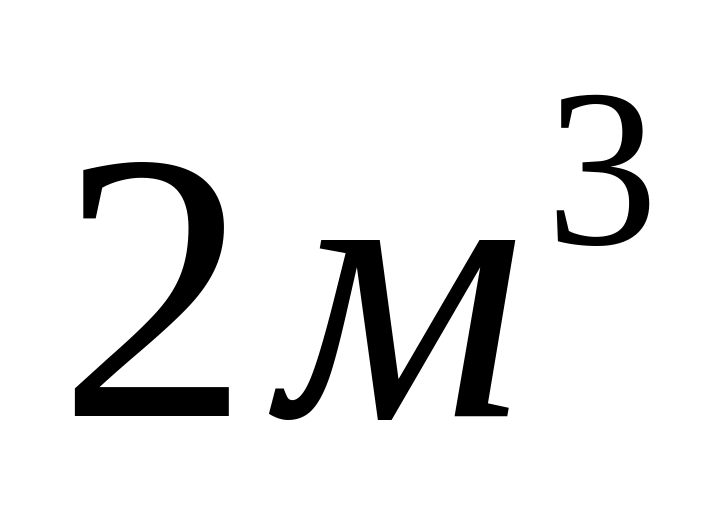 в горизонтальній трубі змінного перерізу
з тиском від
в горизонтальній трубі змінного перерізу
з тиском від
 до
до
 .
.
Чан місткістю
 повинен бути наповненим водою за
повинен бути наповненим водою за
 .
Визначити найменший радіус труби, яка
може бути використана для з’єднання
чану з водонапірною вежею, яка знаходиться
на відстані
.
Визначити найменший радіус труби, яка
може бути використана для з’єднання
чану з водонапірною вежею, яка знаходиться
на відстані
 ,
якщо рівень води у вежі на
,
якщо рівень води у вежі на
 вищий рівня отвору в чані.
вищий рівня отвору в чані.
Який опір відчуває куля діаметром , яка рухається у повітрі зі швидкістю ? Вважати коефіцієнт лобового опору для кулі
 .
.
Обрахувати максимальне значення швидкості потоку води в трубі діаметром
 ,
при якому,цей потік буде залишатись
ламінарним. Критичне значення числа
Рейнольдса для труби приблизно рівне
,
при якому,цей потік буде залишатись
ламінарним. Критичне значення числа
Рейнольдса для труби приблизно рівне
 .
Яке відповідне значення швидкості для
трубки діаметром
.
Яке відповідне значення швидкості для
трубки діаметром
 ?
?
На висоті
 густина атмосфери рівна
густина атмосфери рівна
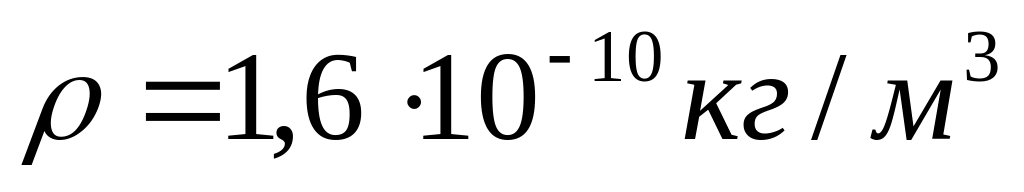 .
Оцінити силу опору, яку відчуває супутник
з поперечним перерізом
.
Оцінити силу опору, яку відчуває супутник
з поперечним перерізом
 і масою
,
який летить на цій же висоті.
і масою
,
який летить на цій же висоті.
Один із методів визначення в’язкості рідин полягає у вимірюванні швидкості падіння кулі в циліндрі, яка заповнена досліджуваною рідиною, і обрахунку
 за формулою Стокса. Прийнявши для кулі
критичне значення числа Рейнольдса
за формулою Стокса. Прийнявши для кулі
критичне значення числа Рейнольдса
 ,
знайти максимальне значення радіуса
стальної кулі, яка може бути використана
в дослідженні при визначенні в’язкості
гліцерину.
,
знайти максимальне значення радіуса
стальної кулі, яка може бути використана
в дослідженні при визначенні в’язкості
гліцерину.
В посудині знаходяться дві ідеальні рідини, які не змішуються, густиною
 і
і
 .
Товщина шарів відповідно
.
Товщина шарів відповідно
 і
і
 .
З поверхні рідини в посудину опускають
кулю. Визначити густину матеріалу кулі,
якщо відомо, що вона досягає дна посудини
в той час, коли швидкість стає рівною
нулю.
.
З поверхні рідини в посудину опускають
кулю. Визначити густину матеріалу кулі,
якщо відомо, що вона досягає дна посудини
в той час, коли швидкість стає рівною
нулю.
У підводному човні на глибині
 утворилася пробоїна, площа якої
.
Яка мінімальна сила
утворилася пробоїна, площа якої
.
Яка мінімальна сила
 потрібна, щоб закрити пробоїну із
внутрішнього боку? Яка сила
потрібна, щоб закрити пробоїну із
внутрішнього боку? Яка сила
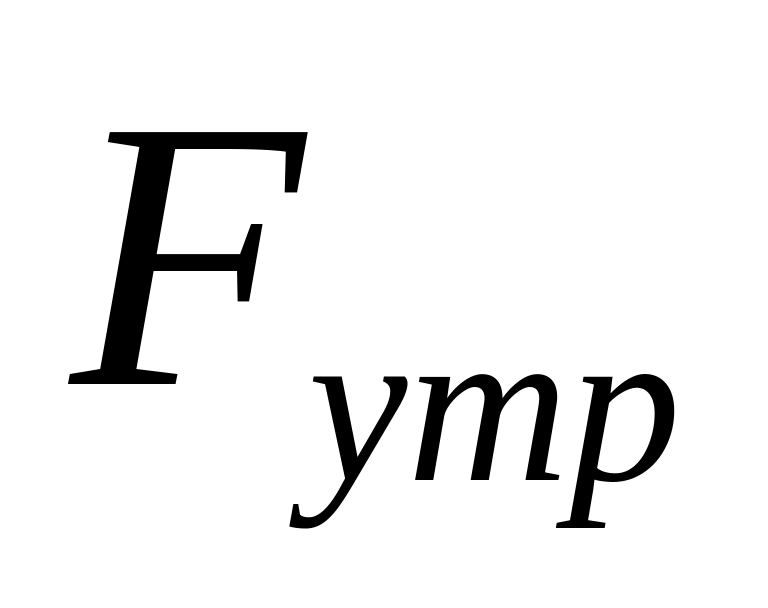 необхідна, щоб утримати латку?
необхідна, щоб утримати латку?
На яку висоту підніметься струмінь води, що витікає зі шланга, якщо надлишковий тиск води у водопроводі
 ?
Опором повітря нехтувати.
?
Опором повітря нехтувати.
Визначити максимальну силу , з якою вітер тисне на стіну будівлі, площа поверхні якої
 .
Густина повітря
.
Густина повітря
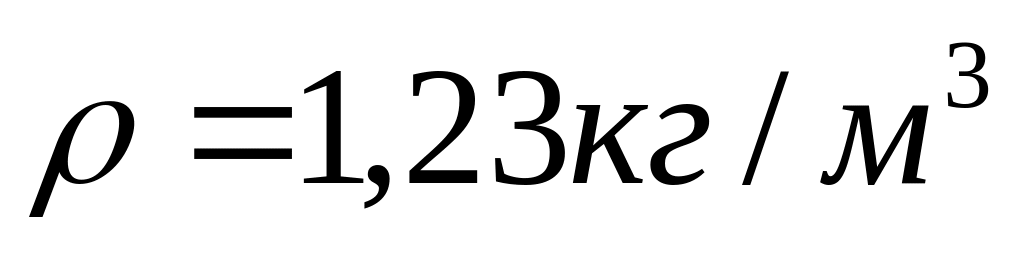 ,
швидкість вітру
,
швидкість вітру
 і він дме перпендикулярно до стіни.
і він дме перпендикулярно до стіни.
За який час можна витиснути ідеальну рідину зі шприца, якщо на поршень діє сила
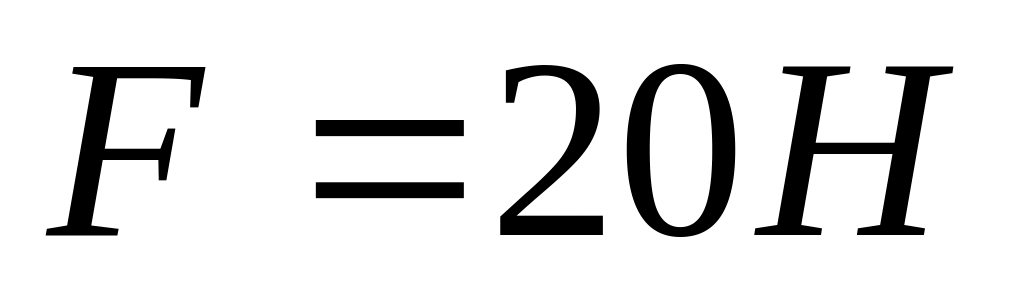 ,
об’єм рідини в шприці
,
об’єм рідини в шприці
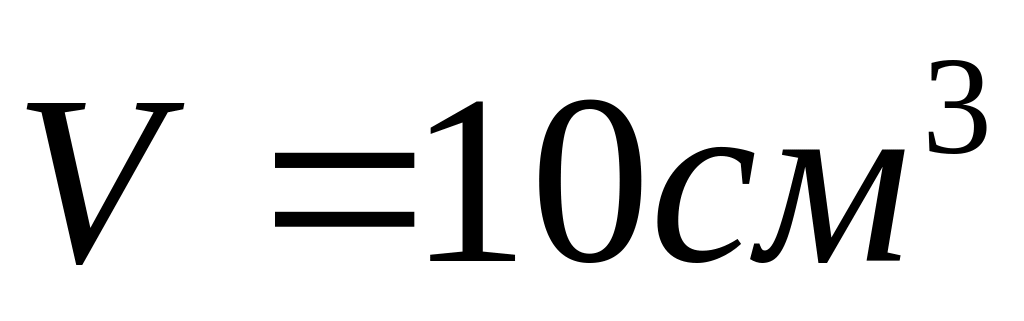 ,
а площі поршня та внутрішнього перерізу
голки відповідно
,
а площі поршня та внутрішнього перерізу
голки відповідно
 ,
,
 ?
Тертя не враховувати. Густина рідини
?
Тертя не враховувати. Густина рідини
 .
.
Циліндричний бак, розташований вертикально, наповнений водою та мазутом. Висота води в баку
 ,
густина мазуту
,
густина мазуту
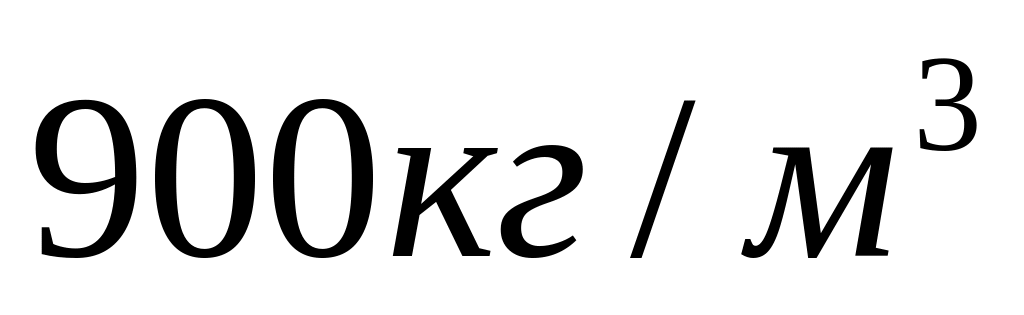 .
У днищі бака зроблено отвір, крізь який
витікає вода з початковою швидкістю
.
У днищі бака зроблено отвір, крізь який
витікає вода з початковою швидкістю
 .
Визначити висоту
шару мазуту в баку. В’язкість води й
мазуту не враховувати.
.
Визначити висоту
шару мазуту в баку. В’язкість води й
мазуту не враховувати.
Центрифуга обертається з кутовою швидкістю
 .
У ній міститься вода, поверхню якої за
даних умов можна розглядати як циліндричну
з радіусом
.
З якою швидкістю
відносно центрифуги витікатиме вода
з отвору, що розміщений на відстані
.
У ній міститься вода, поверхню якої за
даних умов можна розглядати як циліндричну
з радіусом
.
З якою швидкістю
відносно центрифуги витікатиме вода
з отвору, що розміщений на відстані
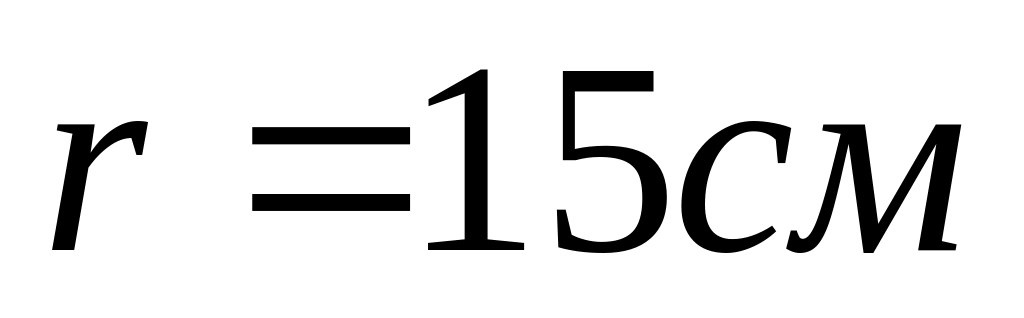 від осі центрифуги?
від осі центрифуги?
Обчислити швидкість усталеного руху краплі води, діаметр якої
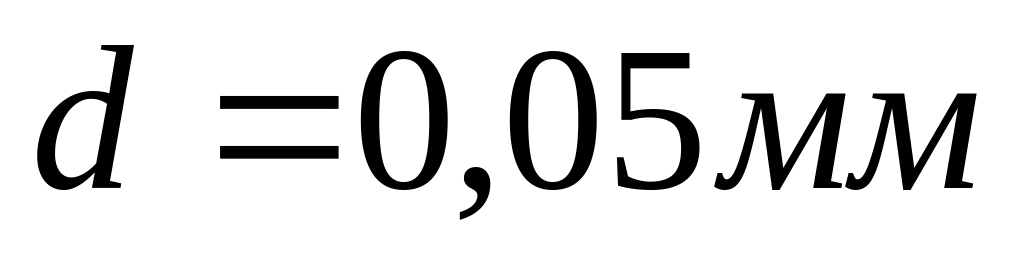 ,
що падає в повітрі. Динамічна в’язкість
повітря
,
що падає в повітрі. Динамічна в’язкість
повітря
 .
Вважати, що рух повітря при обтіканні
краплі є ламінарним.
.
Вважати, що рух повітря при обтіканні
краплі є ламінарним.
Обчислити максимальне значення швидкості потоку води в трубі, що має діаметр
 ,
при якому рух рідини залишається
ламінарним. Вважати, що критичне число
Рейнольдса
,
при якому рух рідини залишається
ламінарним. Вважати, що критичне число
Рейнольдса
 .
В’язкість води
.
В’язкість води
 .
.
За час крізь поперечний переріз труби протікає вода, об’єм якої
 .
Динамічна в’язкість води за даних умов
,
критичне число Рейнольдса
.
Динамічна в’язкість води за даних умов
,
критичне число Рейнольдса
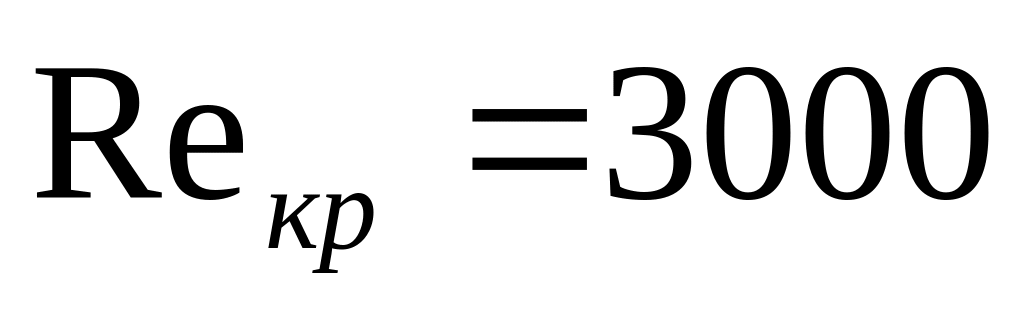 .
Яким має бути діаметр
труби, щоб рух залишався ламінарним?
.
Яким має бути діаметр
труби, щоб рух залишався ламінарним?
Дві кульки однакової густини, радіуси яких
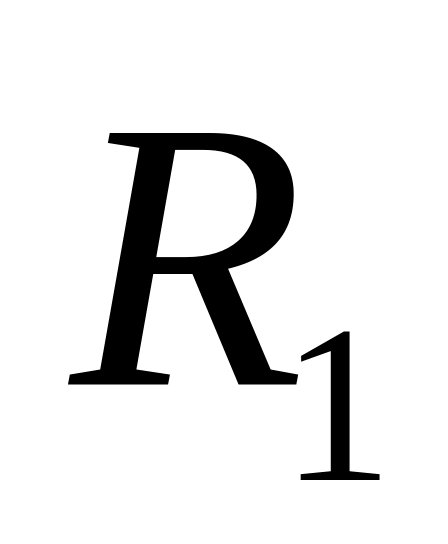 і
і
 ,
рухаються під дією сили тяжіння в
суцільному середовищі з усталеними
швидкостями
і
відповідно. Встановити відношення
швидкостей
,
рухаються під дією сили тяжіння в
суцільному середовищі з усталеними
швидкостями
і
відповідно. Встановити відношення
швидкостей
 кульок, якщо сила опору
рухові пропорційна
-му
степеню добутку площі поперечного
перерізу
кульки та швидкості
її руху? Силою Архімеда нехтувати.
кульок, якщо сила опору
рухові пропорційна
-му
степеню добутку площі поперечного
перерізу
кульки та швидкості
її руху? Силою Архімеда нехтувати.
Знайти швидкість течії по трубі вуглекислого газу, якщо відомо, що за пів години через поперечний переріз труби протікає
 газу. Густину газу прийняти рівним
газу. Густину газу прийняти рівним
 .
Діаметр труби рівний
.
.
Діаметр труби рівний
.
На дні циліндричної посудини є круглий отвір діаметром . Діаметр посудини
 .
Знайти залежність швидкості
зниження рівня води в посудині від
висоти
цього рівня. Знайти чисельне значення
цієї швидкості для висоти
.
Знайти залежність швидкості
зниження рівня води в посудині від
висоти
цього рівня. Знайти чисельне значення
цієї швидкості для висоти
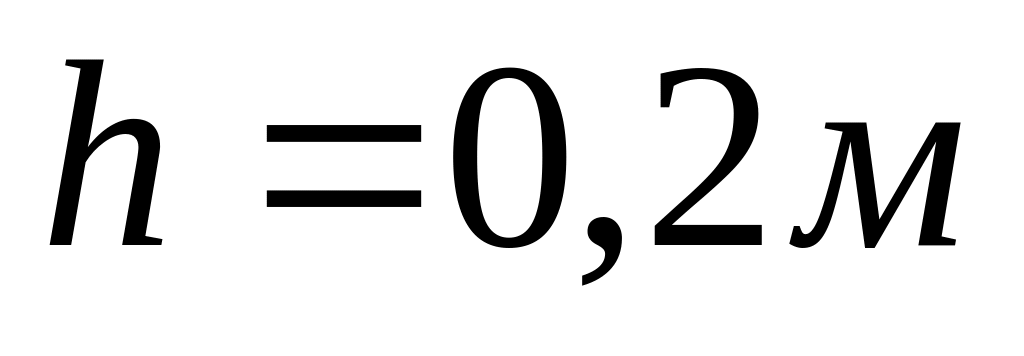 .
.
У посудину ллється вода, при чому за
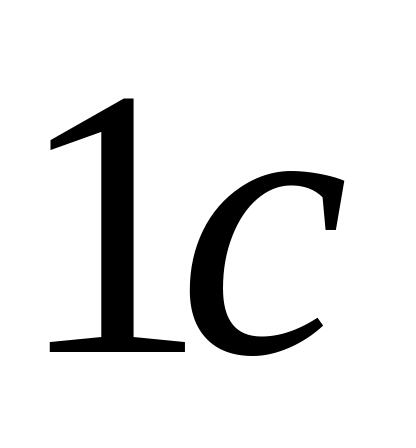 наливається
наливається
 .
Який повинен бути діаметр
отвору на дні посудини, щоб вода в ньому
трималась на постійному рівні, рівному
.
Який повинен бути діаметр
отвору на дні посудини, щоб вода в ньому
трималась на постійному рівні, рівному
 ?
?
Який тиск створює компресор у фарбопульті, якщо струмінь рідини фарби витікає з нього зі швидкістю ? Густина фарби рівна
 .
.
Куля спливає з постійною швидкістю в рідині, густина якої в 4 рази більша густини матеріалу кулі. У скільки разів сила тертя, що діє на спливаючу кулю, більша ваги цієї кулі.
Якої найбільшої швидкості може набути дощова крапля діаметром
 ,
якщо динамічна в’язкість повітря рівна
,
якщо динамічна в’язкість повітря рівна
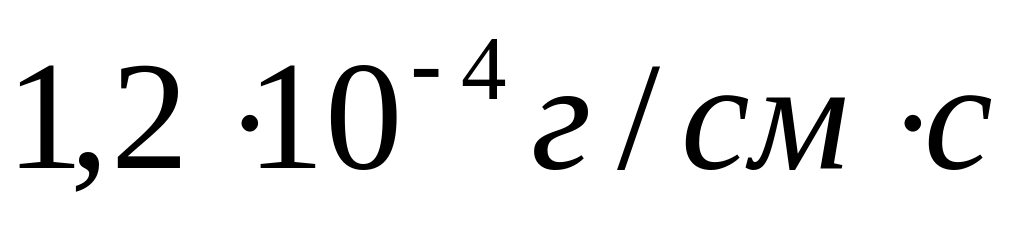 ?
?
Стальна куля діаметром
 падає з постійною швидкістю
падає з постійною швидкістю
 у велику посудину заповнену гліцерином.
Знайти динамічну в’язкість гліцерину.
у велику посудину заповнену гліцерином.
Знайти динамічну в’язкість гліцерину.
Суміш свинцевих дробинок діаметром
 і
відпустили в бак з гліцерином глибиною
в
.
На скільки пізніше впадуть на дно
дробинки меншого діаметру в порівнянні
з дробинками більшого діаметру? Динамічна
в’язкість при температурі досліду
і
відпустили в бак з гліцерином глибиною
в
.
На скільки пізніше впадуть на дно
дробинки меншого діаметру в порівнянні
з дробинками більшого діаметру? Динамічна
в’язкість при температурі досліду
 .
.
Коркова куля радіусом в
 спливає в посудині, наповненою гліцерином.
Чому рівна динамічна і кінематична
в’язкості гліцерину в умовах досліду,
якщо куля спливає з постійною швидкістю
спливає в посудині, наповненою гліцерином.
Чому рівна динамічна і кінематична
в’язкості гліцерину в умовах досліду,
якщо куля спливає з постійною швидкістю
 ?
?
Стальна куля падає в широку посудину, наповнену трансформаторним маслом, густина якого
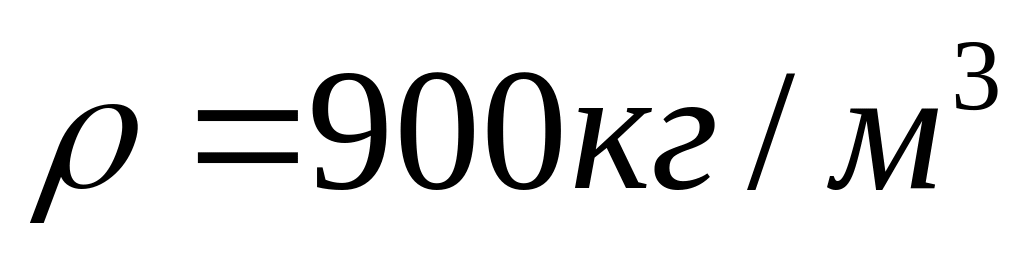 і динамічна в’язкість
і динамічна в’язкість
 .
Вважаючи, що закон Стокса має місце при
.
Вважаючи, що закон Стокса має місце при
 (якщо при обрахуванні
(якщо при обрахуванні
 в якості величини
взяти діаметр кулі), знайти граничне
значення діаметра кулі.
в якості величини
взяти діаметр кулі), знайти граничне
значення діаметра кулі.
Вода тече по трубі, при чому за через поперечний переріз труби протікає
 води. Динамічна в’язкість води в умовах
досліду рівна
води. Динамічна в’язкість води в умовах
досліду рівна
 .
При якому граничному значенні діаметра
труби рух води залишатимиться
ламінарним?
.
При якому граничному значенні діаметра
труби рух води залишатимиться
ламінарним? .
.
Визначити швидкість електропоїзда в момент початку гальмування, вважаючи його рух рівносповільним, якщо він зупинився, пройшовши шлях
 ,
а підвішений у вагоні висок при
гальмуванні відхилився на кут
,
а підвішений у вагоні висок при
гальмуванні відхилився на кут
 від вертикального напрямку.
від вертикального напрямку.
З яким прискоренням повинна рухатися в горизонтальному напрямку похила площина з кутом нахилу
 ,
щоб при відсутності тертя тіло яке
знаходиться на ній не переміщалось
відносно похилої площини?
,
щоб при відсутності тертя тіло яке
знаходиться на ній не переміщалось
відносно похилої площини?
На похилій площині з кутом нахилу лежить тіло. Похила площина рухається з прискоренням
 ,
направленим горизонтально. Чому повинно
бути рівне найменше значення коефіцієнта
тертя
між тілом і похилою площиною, щоб тіло
не ковзало по ній? Чому повинно бути
рівне відповідне значення коефіцієнта
тертя, якщо прискорення похилої площини
буде направлено в протилежний бік?
,
направленим горизонтально. Чому повинно
бути рівне найменше значення коефіцієнта
тертя
між тілом і похилою площиною, щоб тіло
не ковзало по ній? Чому повинно бути
рівне відповідне значення коефіцієнта
тертя, якщо прискорення похилої площини
буде направлено в протилежний бік?
По горизонтальній ділянці дороги їде велосипедист, описуючи дугу радіусом . Під яким кутом до горизонту нахилений велосипедист, якщо його швидкість
 ?
?
З якою найменшою швидкістю може їхати мотоцикліст по внутрішній вертикальній стіні циліндричної будови радіусом
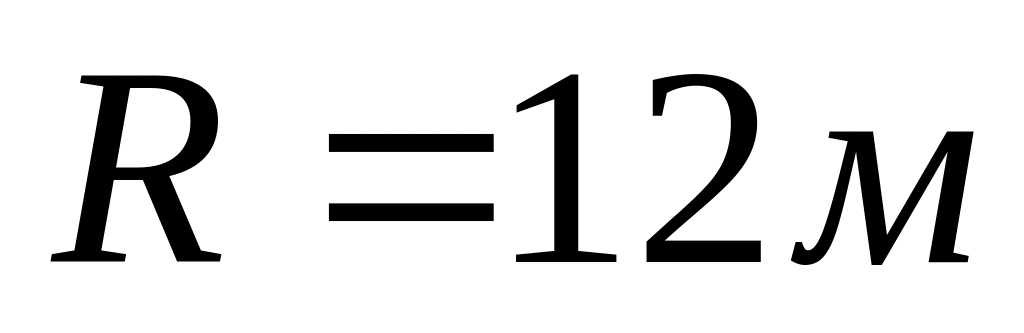 ,
описуючи горизонтальне коло, якщо
коефіцієнт тертя покришок об стіну
,
описуючи горизонтальне коло, якщо
коефіцієнт тертя покришок об стіну
 ,
а центр мас мотоцикліста і мотоцикла
знаходиться на відстані
,
а центр мас мотоцикліста і мотоцикла
знаходиться на відстані
 від стіни?
від стіни?
Електровоз масою
 рухається з півночі на південь в
північній півкулі по горизонтальному
прямолінійному шляху зі швидкістю
рухається з півночі на південь в
північній півкулі по горизонтальному
прямолінійному шляху зі швидкістю
 на широті
.
Визначити горизонтальну складову сили,
з якою електровоз давить на рейки.
на широті
.
Визначити горизонтальну складову сили,
з якою електровоз давить на рейки.
Визначити, на скільки зміниться сила, яка діє на поверхні Землі, якщо тіло масою , яке рухається вздовж екватора зі сходу на захід зі швидкістю , змінить напрям руху на протилежний.
На географічній широті
 тіло вільно падає на Землю з висоти
.
Визначити відхилення тіла під дією
коріолісової сили інерції, викликаної
обертанням Землі.
тіло вільно падає на Землю з висоти
.
Визначити відхилення тіла під дією
коріолісової сили інерції, викликаної
обертанням Землі.
В точці, розміщеній на широті , із рушниці зроблений постріл строго вертикально вгору. Через деякий час куля упала на Землю. Визначити, на скільки змістилась куля, яка упала, від точки пострілу, якщо її початкова швидкість
 .
Опір руху не враховувати.
.
Опір руху не враховувати.
В Ленінграді в Ісааківському соборі встановлений маятник Фуко, довжина якого
 .
На який кут повернеться площина коливань
маятника за час
.
На який кут повернеться площина коливань
маятника за час
 ?
Географічна широта Ленінграду
.
Розв’язати задачу в двох системах
відліку: неінерціальній і геліоцентричній.
?
Географічна широта Ленінграду
.
Розв’язати задачу в двох системах
відліку: неінерціальній і геліоцентричній.
Стержень рухається з деякою постійною швидкістю . Його довжина в нерухомій системі
 ,
а в системі відліку, зв’язаної зі
стержнем,
,
а в системі відліку, зв’язаної зі
стержнем,
 .
Визначити власну довжину стержня і
його швидкість відносно нерухомої
системи відліку.
.
Визначити власну довжину стержня і
його швидкість відносно нерухомої
системи відліку.
Швидкість руху Землі навколо Сонця
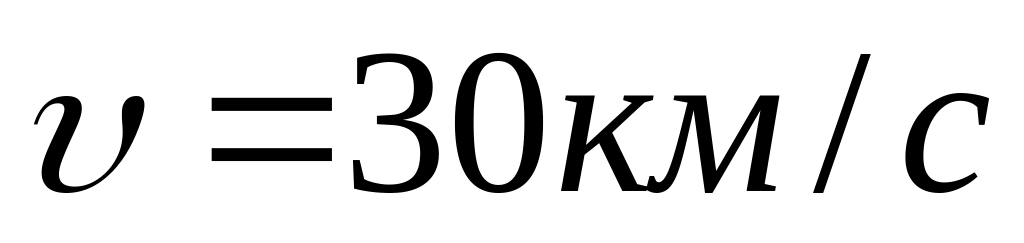 .
Знайти скорочення діаметра Землі в
системі координат, зв’язаною з Сонцем.
.
Знайти скорочення діаметра Землі в
системі координат, зв’язаною з Сонцем.
Реактивний літак летить зі швидкістю
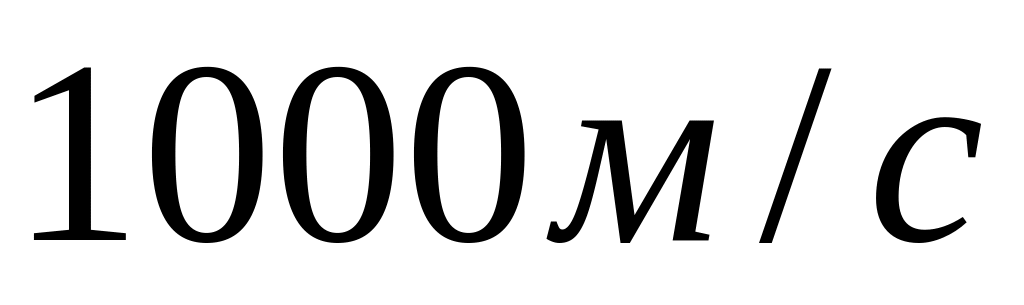 .
На скільки годинник, який знаходиться
в літаку, буде відставати від годинника
на Землі?
.
На скільки годинник, який знаходиться
в літаку, буде відставати від годинника
на Землі?
Користуючись формулами додавання швидкостей у теорії відносності, довести, що додавання швидкостей ніколи не приводить до швидкостей, більших за швидкість світла.
Дві ракети віддаляються від Землі в прямо протилежні сторони зі швидкістю
 відносно
Землі. Знайти, з якою швидкістю рухається
одна ракета в системі відліку, пов'язаною
з іншою ракетою.
відносно
Землі. Знайти, з якою швидкістю рухається
одна ракета в системі відліку, пов'язаною
з іншою ракетою.
Прискорювач надав радіоактивному ядру швидкість
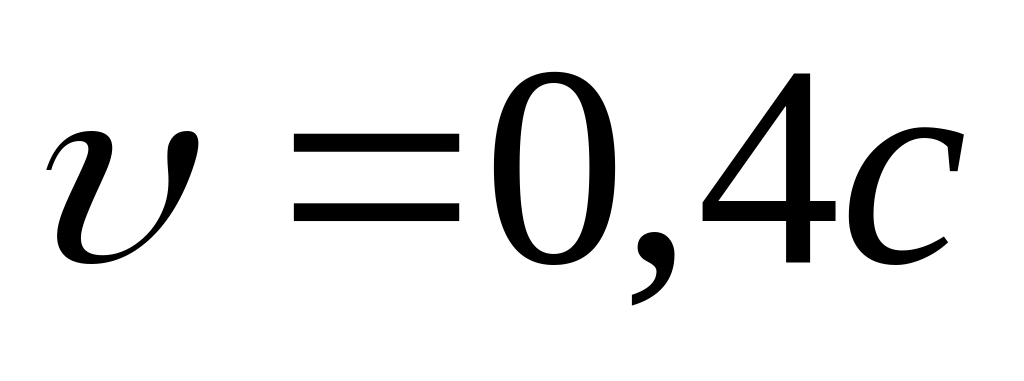 .
В момент вильоту із прискорювача ядро
викинуло в напрямку свого руху
– частинку зі швидкістю
.
В момент вильоту із прискорювача ядро
викинуло в напрямку свого руху
– частинку зі швидкістю
 відносно прискорювача. Знати швидкість
частинки відносно ядра.
відносно прискорювача. Знати швидкість
частинки відносно ядра.
В скільки раз релятивістська маса електрона, який рухається зі швидкістю
 ,
більша за його маса спокою?
,
більша за його маса спокою?
Релятивістська маса тіла, яке рухається з деякою швидкістю, зросла в порівнянні з його масою спокою на
 .
У скільки разів при цьому зменшилась
його довжина?
.
У скільки разів при цьому зменшилась
його довжина?
Релятивістська маса протона, який рухається, в
 раз більша від його маси спокою. Знайти
швидкість протона.
раз більша від його маси спокою. Знайти
швидкість протона.
Знайти відношення кінетичної енергії електрона до його енергії спокою, якщо швидкість електрона
 .
Який релятивістський імпульс електрона?
.
Який релятивістський імпульс електрона?
Повна енергія мезона у
 разів більша його енергії спокою. Яка
швидкість мезона?
разів більша його енергії спокою. Яка
швидкість мезона?
Якій зміні маси відповідає зміна енергії на
 ?
?
Корабель рухається вздовж меридіана на північ зі швидкістю
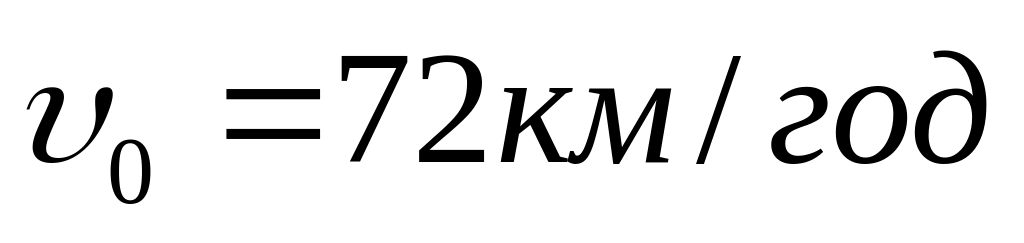 .
Чому дорівнює прискорення
корабля? На яку відстань
.
Чому дорівнює прискорення
корабля? На яку відстань
 і в якому напрямі корабель відхилятиметься
від курсу за
і в якому напрямі корабель відхилятиметься
від курсу за
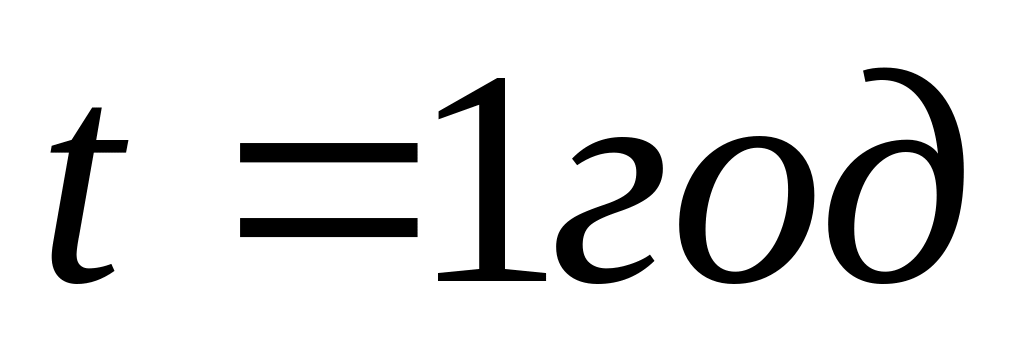 ?
Широта місцевості
?
Широта місцевості
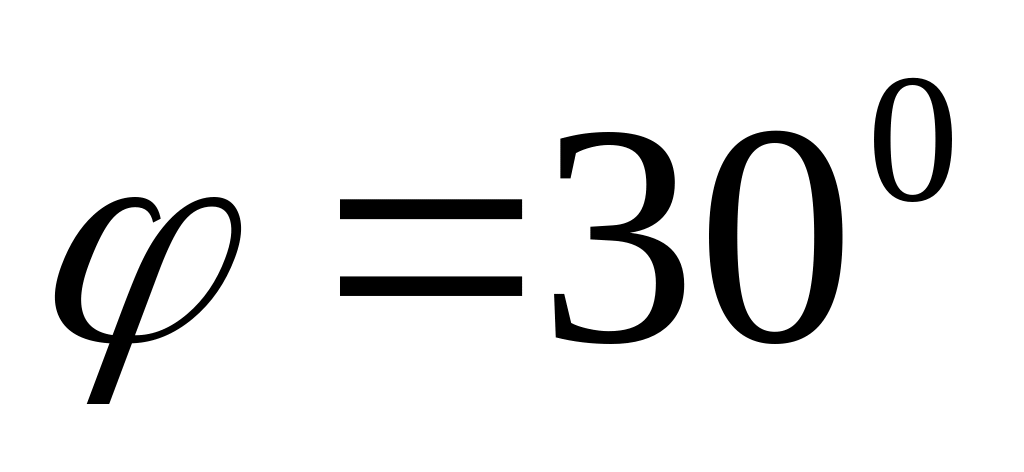 .
Зміною широти знехтувати.
.
Зміною широти знехтувати.
Порожниста сталева кулька піднімається з глибини
 води на поверхню. Швидкість усталеного
руху кульки
.
На яку відстань
води на поверхню. Швидкість усталеного
руху кульки
.
На яку відстань
 і в якому напрямі відносно вертикалі
відхилиться кулька? Широта місцевості
.
і в якому напрямі відносно вертикалі
відхилиться кулька? Широта місцевості
.
Ріка ширина якої
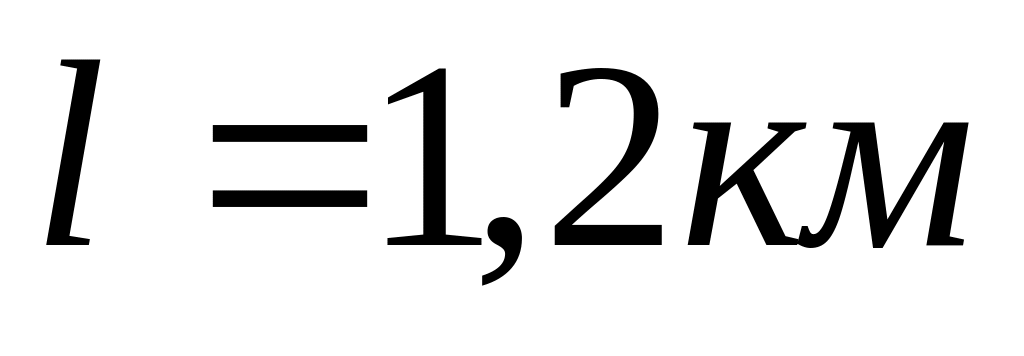 ,
тече з півночі на південь на широті
,
тече з півночі на південь на широті
 .
На скільки метрів рівень
води біля одного берега вищий, ніж біля
іншого? Покласти, що швидкість течії
річки
.
На скільки метрів рівень
води біля одного берега вищий, ніж біля
іншого? Покласти, що швидкість течії
річки
 .
.
В атмосфері Землі на відстані
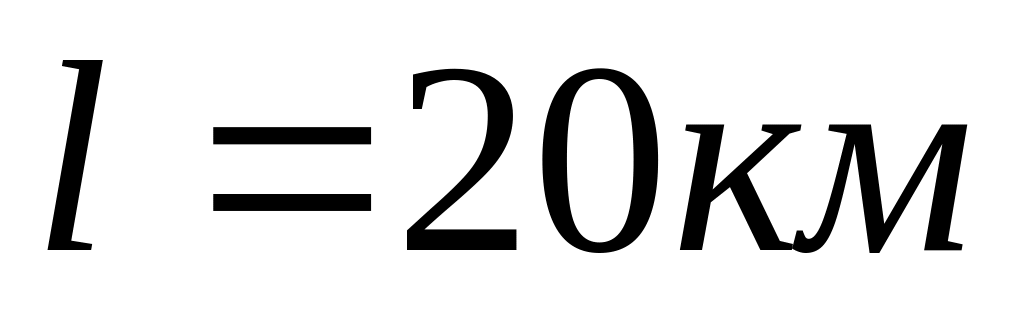 від її поверхні в космічних променях
утворився мюон. Рухаючись зі швидкістю
від її поверхні в космічних променях
утворився мюон. Рухаючись зі швидкістю
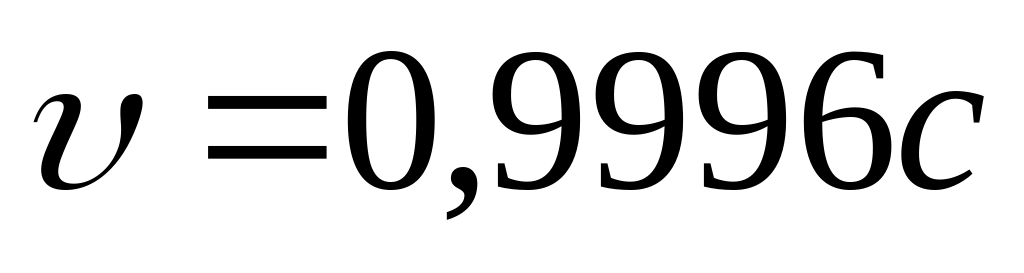 відносно системі відліку, зв’язаної
із Землі, мюон досягає земної поверхні.
До яких розмірів
відносно системі відліку, зв’язаної
із Землі, мюон досягає земної поверхні.
До яких розмірів
 скоротиться ця відстань, якщо не
враховувати сповільнення часу?
скоротиться ця відстань, якщо не
враховувати сповільнення часу?
З якою максимальною швидкістю має рухатися стрижень, щоб відносна похибка, яка допускається при вимірювані його довжини без врахування руху, не перевищувала б
 ?
?
Ребра куба орієнтовані паралельно осям координат. З якою швидкістю куб має рухатися вздовж однієї з осей, для того щоб перетворитися на паралелепіпед із об’ємом втричі меншим, ніж об’єм куба?
Дві частинки рухаються назустріч одна одній зі швидкостями
 і
і
 відносно лабораторної системи відліку.
Визначити відносну швидкість
відносно лабораторної системи відліку.
Визначити відносну швидкість
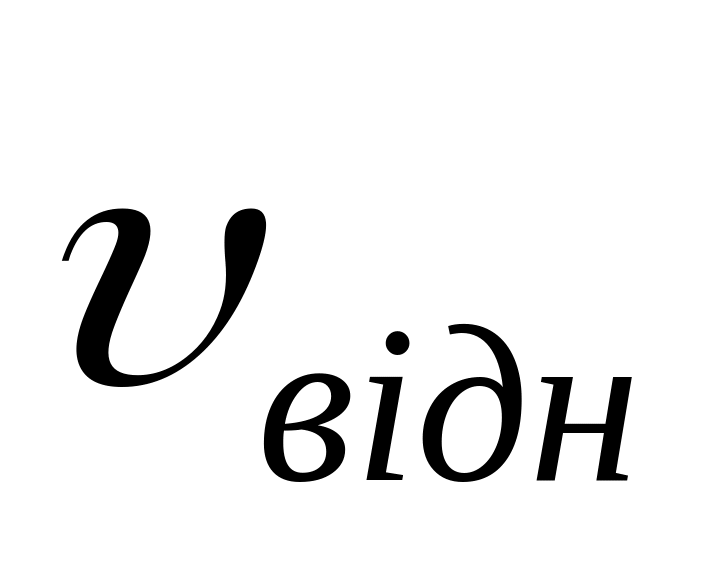 частинок.
частинок.
Одна з частинок рухається відносно лабораторії зі швидкістю
 ,
а інша – зі швидкістю
,
а інша – зі швидкістю
 відносно першої в тому самому напрямі.
Чому дорівнює швидкість
другої частинки відносно лабораторії?
відносно першої в тому самому напрямі.
Чому дорівнює швидкість
другої частинки відносно лабораторії?
Як змінюється імпульс релятивістської частинки у разі зміни її швидкості від
 до
до
 ?
?
Визначити імпульс частинки, кінетична енергія якої
 ,
а швидкість
,
а швидкість
 .
.
Частинка, маса якої
 ,
а швидкість
,
а швидкість
 відносно лабораторії налітає на нерухому
частинку такої самої маси. Визначити
масу спокою
і швидкість
відносно лабораторії налітає на нерухому
частинку такої самої маси. Визначити
масу спокою
і швидкість
 частинки, що утворилася під час непружного
зіткнення.
частинки, що утворилася під час непружного
зіткнення.
При якій відносній швидкості руху релятивістське скорочення довжини, тіла яке рухається, становить .
Яку швидкість повинно мати тіло, яке рухається, щоб його поздовжні розміри зменшились удвічі?
На скільки збільшиться маса -частинки при прискоренні її від початкової швидкості, рівній нулю, до швидкості, рівній
 швидкості світла?
швидкості світла?
Яку прискорюючу різницю потенціалів повинен пройти електрон, щоб його швидкість склала
 швидкості світла?
швидкості світла?
Яку прискорюючу різницю потенціалів повинен пройти протон, щоб його поздовжні розміри стали менші удвічі?
Знайти швидкість мезону, якщо його повна енергія в
 разів більша за енергію спокою.
разів більша за енергію спокою.
Синхрофазотрон дає пучок протонів з кінетичною енергією в
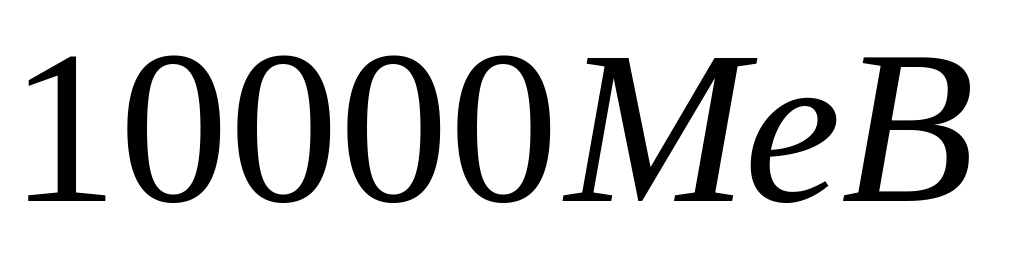 .
Яку частину швидкості світла складає
швидкість протонів в цьому пучку?
.
Яку частину швидкості світла складає
швидкість протонів в цьому пучку?
