3.9. Механічні коливання і хвилі. Елементи акустики

Гармонічне коливання описується законом: або , де – значення величини, що здійснює коливання, у даний момент часу , – амплітуда коливань, – фаза коливань, – циклічна частота ( , – період), – початкова фаза коливань.

У подальших формулах використовується закон косинуса.

Швидкість коливального руху:

.

Прискорення коливального руху:

.

Кінетична енергія коливальної системи:

.

Потенціальна енергія коливальної системи:

.

Повна енергія коливальної системи:

.

Додавання двох гармонічних коливань однакового напрямку з однаковими частотами:

а) амплітуда результуючого коливання: ;

б) початкова фаза результуючого коливання: ;

Рівняння траєкторії точки, що одночасно бере участь у двох коливаннях однакової частоти, напрями яких є взаємно перпендикулярними:

.

Вільні коливання простих коливальних систем описуються диференціальним рівнянням: .

Періоди гармонічних коливань простих коливальних систем:

а) пружинний маятник з коефіцієнтом жорсткості і масою : ;

б) математичний маятник завдовжки : ;

в) фізичний маятник з моментом інерції відносно вісі коливань і відстанню від центра мас тіла до точки підвісу: ;

г) крутильний маятник з моментом інерції відносно вісі коливань і модулем кручення : .

Диференціальне рівняння згасаючих коливань: , його розв’язок (для ) , де – коефіцієнт згасання, – циклічна частота згасаючих коливань ( ).

Коефіцієнт згасання: , де r – коефіцієнт опору.

Логарифмічний декремент згасання: .

Добротність коливальної системи: .

Диференціальне рівняння вимушених коливань: , де – амплітуда зовнішньої сили. Рівняння руху: , де – зсув фаз між силою і зміщенням.

Амплітуда вимушених коливань: .

Резонансна частота: .

Резонансна амплітуда: .

Рівняння плоскої стаціонарної хвилі: , де – хвильове число, ; тут – довжина хвилі, – фазова швидкість поширення хвилі, .

Фазова швидкість поздовжніх пружних хвиль у твердих тілах:

,

де – модуль Юнга, – густина середовища.

Фазова швидкість поширених хвиль у твердих тілах:

,

де – модуль зсуву.

Швидкість зсуву в ідеальних газах (формула Лапласа):

,

де – показник адіабати ( ); – універсальна газова стала, –температура, – молярна маса газу, і – тиск і густина газу.

Швидкість поперечних хвиль у струмі:

,

де – сила натягу струни; – густина матеріалу струни, – площа її поперечного перерізу.

Рівень гучності у децибелах (дБ):

,

де – інтенсивність звуку; – поріг гучності ( ).

Згасання хвилі у децибелах

.

Акустичний ефект Доплера

,

де – частота, що реєструє приймач, – частота, що випромінює джерело, – швидкість звуку, і – відповідно швидкості приймача і джерела звуку відносно середовища, в якому поширюються звукові хвилі. Верхні знаки беруть у разі зближення джерела приймача, нижні – віддалення.

4. Приклади розв’язування задач

4.1. Радіус-вектор матеріальної точки змінюється з часом за законом , де , – орти осей і . Визначити для моменту часу : 1) модуль швидкості; 2) модуль прискорення.

Дано:

– ? – ?

Аналіз

За означенням миттєва швидкість визначається за формулою:

.

Миттєве прискорення матеріальної точки визначається:

.

З врахуванням, що , маємо , .

Оскільки , то .

Відповідно для прискорення: , і .

Отже, .

Обчислення:

, .

Відповідь: модуль швидкості для моменту часу рівний , а модуль прискорення .

4.2. Колесо автомашини обертається рівносповільнено. За час воно змінило частоту від до . Визначити: 1) кутове прискорення колеса; 2) число повних обертів, зроблених за цей час.

Дано:	СI
– ? – ?

Аналіз

Кутова швидкість під час обертального руху змінюється за законом: .

Враховуючи, що , то . Остаточно:

Кінематичне рівняння обертального руху: , де – кутове переміщення матеріальної точки. Згідно умови задачі: .

Враховуючи, що , то . Звідки .

Обчислення:

, .

Відповідь: кутове прискорення колеса , кількість повних обертів колеса .

4.3. Уздовж похилої площини, що утворює з горизонтом кут , піднімають тіло. Коефіцієнт тертя становить . Під яким кутом до похилої площини потрібно спрямувати силу, щоб вона була найменшою?

Дано:

– ?

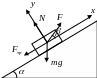А наліз

Оскільки в умові задачі не зазначено, що тіло рухається з прискоренням, то вважатимемо рух тіла рівномірним ( і ).

Згідно з другим законом Ньютона .

Спроектуємо сили на координатні вісі і .

.

.

За означенням і, враховуючи, що , маємо

.

З отриманого рівняння виокремимо силу : .

Сила буде мінімальною, якщо знаменник матиме максимальне значення. Залежність сили від кута дослідимо на екстремум. Першу похідну від знаменника прирівняємо до нуля і отримаємо:

, звідси .

Ми знайшли критичну точку функції . Друга похідна від знаменника при менша за нуль. Це означає, що точка є максимумом. А отже сила , прикладена до тіла, має мінімальне значення.

Відповідь: сила повинна бути спрямована під кутом до похилої площини.

4.4. Знайти першу космічну швидкість для Землі, тобто мінімальну швидкість, яку треба надати тілу, щоби вивести його на навколоземну орбіту.

Дано:

– ?

Аналіз

На супутник, що рухається по колу радіуса , діє сила тяжіння Землі, яка є доцентровою силою і надає йому нормального прискорення . За другим законом Ньютона: , де – маса супутника, – маса Землі, – радіус Землі. Звідси .

Якщо висота над Землею мала порівняно з радіусом Землі , поблизу поверхні Землі .

Обчислення:

.

Відповідь: перша космічна швидкість .

4.5. При центральному пружному ударі тіло масою стикається з нерухомим тілом масою , в результаті чого швидкість першого тіла зменшується в 2 рази. Визначити: 1) у скільки разів маса першого тіла більша за масу другого тіла; 2) кінетичну енергію другого тіла після удару, якщо кінетична енергія першого тіла до удару була рівна .

Дано:

– ? – ?

Аналіз

З апишемо закони збереження імпульсу і енергії для абсолютно пружного удару двох тіл. Оскільки друге тіло до удару перебувало в стані спокою, то

Враховуючи, що , та , маємо:

З верхнього рівняння ; з нижнього: .

Оскільки , то , звідки . Отже, .

Рівняння (2) запишемо у вигляді: .

Враховуючи, що , тоді . Отже,

.

Обчислення:

.

Відповідь: маса першого тіла більша за масу другого тіла у рази, кінетична енергія другого тіла після удару рівна .

4.6. Куля масою , що летить горизонтально зі швидкістю , попадає в балістичний маятник масою і застряє в ньому. На яку висоту підніметься маятник після удару?

Дано:	СI
– ?

Аналіз

Запишемо закони збереження кількості руху і енергії з урахуванням умови задачі: 1) удар непружний; 2) рух здійснюється в одному напрямку; 3) кінетична енергія повністю переходить в потенціальну.

де – швидкість маятника з кулею.

Розв’язавши систему рівнянь, одержимо:

.

Обчислення:

.

Відповідь: висота, на яку підніметься балістичний маятник, .

4.7. Колесо, радіус якого і маса скочується без тертя по похилій площині довжиною і кутом нахилу . Визначити момент інерції колеса, якщо його швидкість в кінці руху рівна .

Дано:	СI
– ?

Аналіз

За законом збереження енергії маємо:

.

Оскільки в умові задачі задано лінійну швидкість колеса, то використаши заміну: , одержимо . Враховуючи, що , маємо

Отже,

Обчислення:

.

Відповідь: момент інерції колеса .

4.8. Два вантажі масами і з’єднані невагомою ниткою, перекинутою через блок масою . Знайти прискорення , з яким рухаються вантажі, і силу натягу і нитки, до якої підвішені вантажі. Блок вважати однорідним диском. Тертям знехтувати.

Дано:

– ? – ? – ?

А наліз

На кожен із вантажів діють дві сили: сила тяжіння, яка направлена вниз, і сила натягу нитки, яка направлена вгору. Рівнодійні цих сил спричинюють рівноприскорений рух тіл. Згідно з другим законом Ньютона, маємо:

Обертання блоку відбувається згідно основного закону динаміки обертального руху твердого тіла:

,

де , І= . Враховуючи, що = , де – радіус блока, маємо

або

Спроектувавши рівняння (1) і (2) на вісь і, додавши до них рівняння (3), отримуємо:

Із перших двох рівнянь системи визначаємо і підставляємо у третє: Звідки :

З перших рівнянь системи знаходимо сили натягу нитки:

; .

Обчислення:

;

; .

Відповідь: прискорення, з яким рухаються вантажі, , сили натягу нитки відповідно: і .