3.6. Механіка рідин і газів

Рівняння нерозривності течії:

,

де – площа -го поперечного перерізу, – швидкість ідеальної рідини при стаціонарному русі на цьому перерізі.

Рівняння Бернуллі для ідеальної рідини:

,

де – густина рідини, – її швидкість, – прискорення вільного падіння, – статичний тиск.

Формула Торрічеллі:

,

де – швидкість витікання рідини з отвору, який знаходиться на висоті до вільної поверхні рідини.

Сила реакції рідини, що витікає (реактивна сила):

,

де S – площа перерізу отвору.

Сила, що діє на занурене в рідину (газ) тіло (закон Архімеда):

,

де – густина рідини (газу), – об’єм зануреної частини тіла (об’єм рідини або газу, яку витіснило тіло).

Сила в’язкого тертя (закон Ньютона):

де – динамічна в’язкість рідини, – площа поверхні контакту шарів рідини; – модуль градієнта швидкості (у напрямку нормалі до осі ).

Сила опору, що діє на рухому кульку у в’язкому середовищі або при обтіканні речовини нерухомої кульки (закон Стокса):

,

де – радіус кульки, – швидкість руху кульки або швидкість обтікаючої речовини.

При ламінарній течії об’єм рідини (газу) , що протікає за час крізь трубку завдовжки і радіуса визначається за формулою Пуазейля:

,

де – різниця тисків на кінцях трубки.

Лобовий опір тіла, що міститься в ламінарному потоці в’язкої рідини:

,

де – швидкість течії, – коефіцієнт, що залежить від форми і розмірів тіла.

Для турбулентного потоку при великих швидкостях течії лобовий опір:

,

де – коефіцієнт лобового опору, що залежить від форми тіла та числа Рейнольдса, S – найбільша площа перерізу тіла перпендикулярна до потоку течії, – густина середовища.

Число Рейнольдса

,

де – величина, що характеризує лінійні розміри тіла, – кінематична в’язкість .

3.7. Рух тіл в неінерціальних системах відліку

Рівняння руху частинки відносно неінерціальної системи відліку

,

де – прискорення частинки в системі відліку , – рівнодійна всіх сил, що діють на частинку з боку інших тіл, – сила інерції.

Рівняння руху частинки в неінерціальній системі, що обертається зі сталою кутовою швидкістю відносно нерухомої осі:

,

де – вектор, що лежить у площині обертання і проведений від осі обертання до частинки, – швидкість частинки відносно системи відліку .

Сила Коріоліса: .

3.8. Елементи спеціальної теорії відносності (ств)

Перетворення Лоренца у випадку, коли система відліку , рухається зі швидкістю в заданому напрямку осі Ох системи (осі і – збігаються, осі і та і паралельні одна одній).

, ; ;

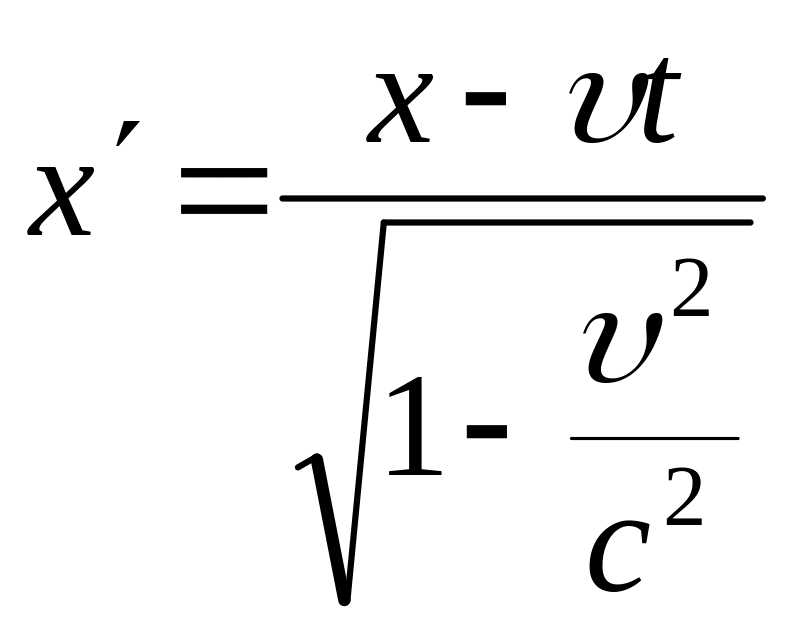Релятивістське скорочення довжини тіла: , де – довжина тіла в системі відліку .

Сповільнення ходу годинника, що рухається: , де – інтервал часу в системі відліку .

Релятивістська маса та релятивістський імпульс:

, .

Рівняння релятивістської динаміки частинки: .

Енергія релятивістської частинки:

а) енергія спокою: ;

б) повна енергія: ;

в) кінетична енергія: .

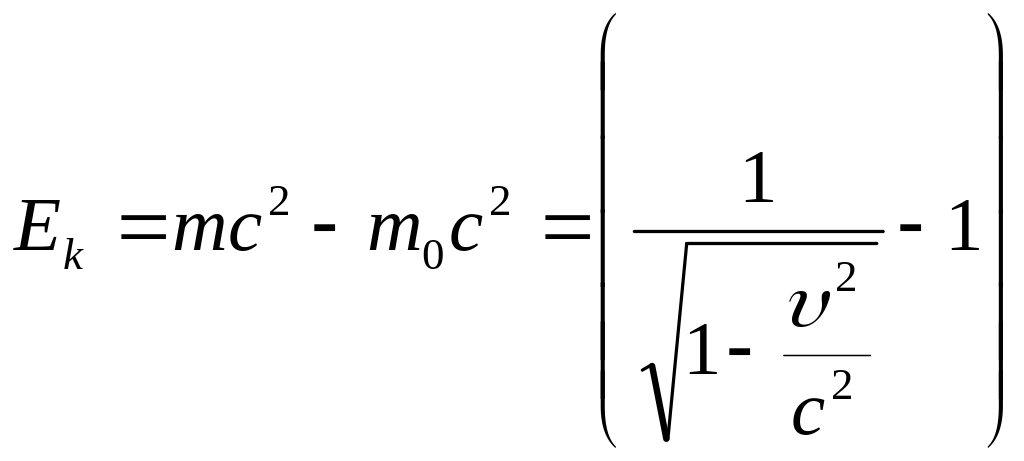Зв'язок між енергією та імпульсом релятивістської частинки:

, .