12.2. Методы решения системы дифференциальных уравнений

Одним из способов решения системы есть метод исключения, который предусматривает исключение 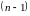неизвестных функций, в результате чего система сводится к дифференциальному уравнению -го порядка относительно одной из неизвестных функций.

Пример 1.

Найдем решение системы дифференциальных уравнений:

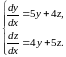
Это нормальная система линейных дифференциальных уравнений. Применим для ее решения метод исключения. Продифференцируем первое уравнение системы: .

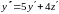Учитывая второе уравнение, имеем:

.

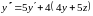
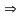
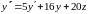По первому уравнению системы определяем, что ,

тогда: .

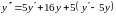
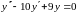Следовательно, для определения функции 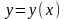мы получили однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение соответствующего однородного уравнения имеет вид: 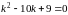. Отсюда определяем корни: , .

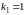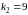Теперь записываем общее решение для функції :

.

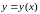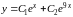Теперь находим функцию 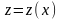, подставив в первое уравнение системы и 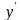, но сначала найдем : .

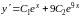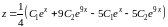, или .

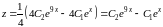Следовательно, общее решение системы дифференциальных уравнений: , .

Рассмотрим еще один метод решения системы дифференциальных уравнений, который называется алгебраическим.

Пусть задана нормальная система дифференциальных уравнений первого порядка

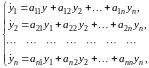
где 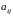– постоянные величины, 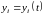– неизвестны функции .

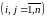Систему можно записать как матричное уравнение:

,

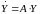где

, , .

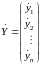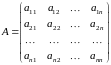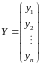Частные решения системы будем искать в виде совокупности показательных функций: 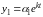, , 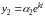..., , 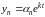где 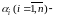неопределенные постоянные, которые нужно найти.

Подставляя эти функции в систему и сокращая на множитель 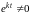, получим систему линейных уравнений относительно :

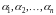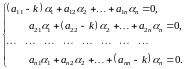
Найдем определитель этой системы:

.

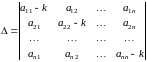Если 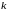такое, что определитель 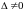, то система уравнений имеет только тривиальное решение: .

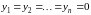Нетривиальное решение система будет иметь лишь при таких , при которых определитель этой системы будет равен нулю.

Следовательно, для определения мы приходим к уравнению -го порядка:

.

Это уравнение называется характеристическим уравнением системы дифференциальных уравнений, его корни – корнями характеристического уравнения.

Рассмотрим только случай, когда корни характеристического уравнения действительные и разные.

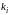
Для каждого корня 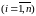записывают систему и определяют коэффициенты 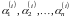. Поскольку ранг матрицы системы равен 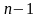, то один из коэффициентов можно выбрать произвольно. Будем считать его равным единице.

Тогда получаем частные решения системы:

для : , , ..., ;

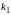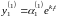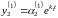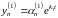для : , , ..., ;

…………………………………………………………….

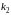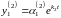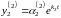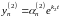для : , , ..., .

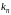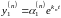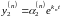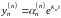Систему частных решений

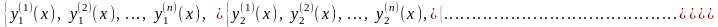
называют фундаментальной системой решений на интервале , если определитель

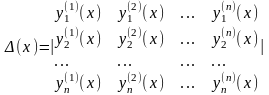
не равен нулю.

Соответственно, общее решение системы имеет вид:

,

,

……………………………………..

,

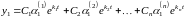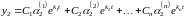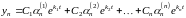где – произвольные постоянные.

Пример 2.

Найдем общее решение системы дифференциальных уравнений:

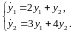
Будем искать частые решения этой системы в виде 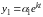и 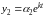. Для определения неизвестных коэффициентов 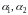этих функций составляем характеристическое уравнение:

,

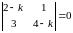откуда

.

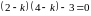
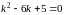Корни уравнения , .

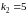При система принимает вид:

Отсюда .

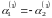Пусть 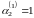, тогда .

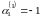Следовательно, имеем решения: , .

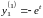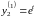При система имеет вид:

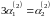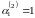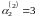Отсюда . Считая , получим . Тогда:

, .

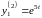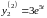Таким образом, мы получили фундаментальную систему решений:

, ,

, .

Следовательно, общее решение системы имеет вид:

,

.
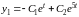
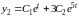