- •Лекция 9. Дифференциальные уравнения первого порядка
- •9.1. Понятие дифференциального уравнения и его решения
- •9.2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •9.3. Однородные дифференциальные уравнения
- •9.4. Линейные дифференциальные уравнения первого порядка
- •9.5. Дифференциальные уравнения Бернулли
- •Лекция 10. Линейные дифференциальные уравнения второго порядка
- •10.1. Дифференциальные уравнения второго порядка
- •10.2. Дифференциальные уравнения второго порядка, которые допускают понижение порядка
- •Лекция 11. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •11.1. Однородные уравнения второго порядка с постоянными коэффициентами
- •Частные решения неоднородного уравнения
- •Лекция 12. Системы дифференциальных уравнений
- •12.2. Методы решения системы дифференциальных уравнений
- •Лекция 13. Числовые ряды
- •13.1. Частные суммы ряда. Необходимое условие сходимости ряда
- •Ряд геометрической прогрессии
- •Гармонический ряд
- •13.2. Достаточные признаки сходимости рядов с положительными членами: признак сравнения, Даламбера, Коши, интегральный признак Маклорена – Коши
- •Признак сравнения
- •Признак Даламбера
- •Радикальный признак Коши
- •Интегральный признак Маклорена – Коши
- •Лекция 14. Знакопеременные ряды.
- •14.1. Абсолютная и условная сходимость рядов
- •14.2. Знакочередующиеся ряды. Теорема Лейбница
- •Лекция 15. Степенные ряды
- •15.1. Теорема Абеля. Радиус сходимости степенного ряда
- •Лекция 16. Ряды Тейлора и Маклорена
- •16.1. Разложение элементарных функций в ряды Тейлора и Маклорена
- •16.2. Применение степенных рядов степеней в приближенных вычислениях
- •Вычисление с помощью знакочередующихся рядов
- •Вычисление с помощью знакоположительных рядов
- •Лекция 17. Элементы финансовой математики
- •17.1. Общие положения финансовой математики
- •17.2. Наращение по простой процентной ставке
- •17.2. Дисконтирование и учет по простым процентным ставкам
- •17.3. Сложные проценты
9.4. Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной первого порядка, а именно:
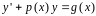 ,
(9.13)
,
(9.13)
где
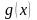 – свободный член уравнения;
– свободный член уравнения;
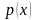 и
– известные и непрерывные функции
независимой переменной
(они также могут быть постоянными).
и
– известные и непрерывные функции
независимой переменной
(они также могут быть постоянными).
Метод Бернулли
Найдем решение уравнения в виде
произведения двух неизвестных функций:
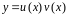 .
Для первой производной этого
соотношения получим выражение:
.
Для первой производной этого
соотношения получим выражение: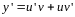 .
.
Таким образом, исходное уравнение (9.13) будет иметь вид:
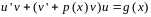 .
.
Выбрав в качестве
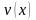 любое частное решение уравнения:
любое частное решение уравнения:
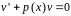 ,
,
для поиска неизвестной функции
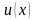 получим уравнение:
получим уравнение:
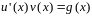 .
.
Таким образом, исходное уравнение свелось к решению системы двух дифференциальных уравнений:
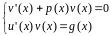 ,
(9.14)
,
(9.14)
оба уравнения которой составляют уравнения с разделяющимися переменными. Решив первое уравнение системы, найдем функцию :
 ,
,
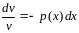 ,
,
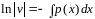 ,
,
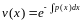 ,
,
поскольку нас интересует любое частное решение.
Подставляя найденное решение
во второе уравнение системы, получим:
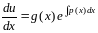 ,
,
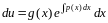 .
.
Откуда: 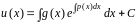 .
.
Таким образом, общее решение линейного уравнения имеет вид:
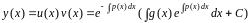 .
(9.15)
.
(9.15)
Пример
9. Найти решение уравнения
 .
.
Решение.
Имеем уравнение вида (9.13).
Применяем
подстановку
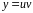 ,
где
,
где
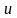 и
и
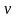 – функции от
.
– функции от
.
Тогда
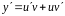 .
.
Подставляя
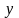 и
и
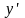 в данное уравнение, получим:
в данное уравнение, получим:
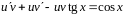 .
.
Сгруппируем члены, которые содержат
,
и вынесем
за скобки, а именно:
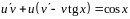 .
.
Дальше функцию
 выбираем так, что
выбираем так, что
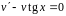 ,
тогда
,
тогда
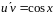 .
.
Следовательно, для нахождения и имеем систему:
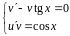 .
(9.16)
.
(9.16)
Решая первое уравнение, найдем
:
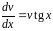 ,
или
,
или
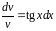 .
.
Интегрируем обе части:
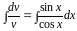 ,
,
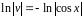 ,
,
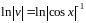 .
.
Откуда
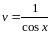 .
.
Найденную функцию подставляем во второе уравнение системы (9.16) и находим :
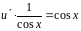 ,
,
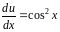 ,
,
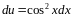 .
.
Интегрируем: 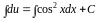 ,
,
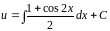 .
.
Следовательно,
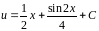 .
.
Таким образом,
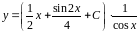 .
.
9.5. Дифференциальные уравнения Бернулли
Некоторые уравнения в результате замены неизвестной функции могут быть приведены к линейному дифференциальному уравнению, например уравнение Бернулли, которое имеет вид:
 ,
(9.17)
,
(9.17)
где
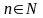 .
.
В этом уравнении
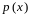 и
и
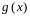 – некоторые непрерывные функции,
которые могут быть и постоянными.
Уравнение Бернулли является нелинейным
уравнением, поскольку неизвестная
функция
– некоторые непрерывные функции,
которые могут быть и постоянными.
Уравнение Бернулли является нелинейным
уравнением, поскольку неизвестная
функция
 в правой части уравнения нелинейная.
в правой части уравнения нелинейная.
Разделив обе части уравнения на
 ,
получим:
,
получим:
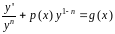 .
(9.18)
.
(9.18)
Заменим функцию
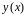 на новую функцию
на новую функцию
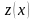 с помощью выражения:
с помощью выражения:
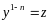 .
Для первой производной этого соотношения
получим:
.
Для первой производной этого соотношения
получим:
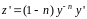 .
Подставим полученные соотношения в
исходное уравнение. Будем иметь линейное
дифференциальное уравнение относительно
функции
.
Подставим полученные соотношения в
исходное уравнение. Будем иметь линейное
дифференциальное уравнение относительно
функции
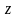 ,
а именно:
,
а именно:
 ,
,
решение которого рассмотрено выше.
Пример
10. Найти решение
уравнения
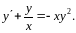
Решение.
По условию имеем уравнение Бернулли (9.17).
Преобразуем
его к линейному, применяя замену
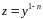 .
В нашем примере
.
В нашем примере
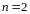 ,
поэтому
,
поэтому
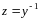 или
или
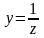 ,
тогда
,
тогда
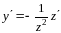 .
.
Уравнение
принимает вид:
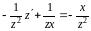 ,
,
или после умножения на
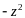 :
:

Теперь имеем линейное уравнение относительно .
Решение уравнения ищем в виде
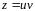 ,
отсюда
,
отсюда
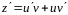 .
Подставляя
и
.
Подставляя
и
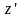 в уравнение, получаем:
в уравнение, получаем:
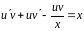 ,
или
,
или
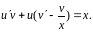
Это уравнение заменяем системой уравнений:
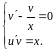 .
.
Из первого уравнения системы найдем :
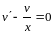 ,
или
,
или
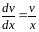 ,
откуда
,
откуда
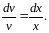
Таким
образом,
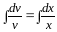 ,
,
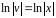 ,
то есть
,
то есть
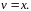
Из второго уравнения системы найдем :
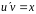 ,
или
,
или
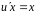 ,
,
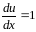 ,
,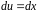 .
.
Интегрируя,
имеем
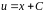 .
.
Таким образом:
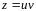 ,
,
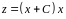 .
.
Возвращаемся к переменной :
 ,
или
,
или