Лекция 9. Дифференциальные уравнения первого порядка
9.1. Понятие дифференциального уравнения и его решения
Уравнение вида:
,
(9.1)
которое
связывает аргумент
,
неизвестную функцию
и ее производные, называется дифференциальным
уравнением.
Порядком дифференциального уравнения называют порядок наивысшей производной, которую содержит в себе уравнение, а ее степень называется степенью дифференциального уравнения.
Если неизвестная функция, которая
входит в дифференциальное уравнение,
является функцией более чем одной
переменной, то дифференциальное уравнение
называется уравнением в частных
производных. Решением дифференциального
уравнения называют функцию
,
подстановка которой в уравнение
превращает его в тождество. График
решения называется интегральной
кривой. Решить или проинтегрировать
данное дифференциальное уравнение
значит найти все его решения. Уравнение
(9.1) имеет множество
решений.
Пример 1. Показать, что функция
является решением уравнения
Решение.
Находим
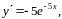
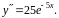Подставляем в заданное уравнение
то есть функция
действительно является решением
заданного дифференциального уравнения.
Общим
решением дифференциального уравнения
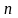-го
порядка называется его решение:
,
(9.2)
которое содержит
независимых произвольных постоянных
.
Если общее решение задано в неявном виде:
,
(9.3)
то оно называется общим интегралом.
Частным решением дифференциального уравнения называется решение, которое получается из общего решения, если свободным постоянным придавать некоторые значения.
Дифференциальным уравнением первого порядка называется уравнение вида:
,
(9.4)
или
.
(9.5)
Уравнение (9.5) – уравнение первого порядка, разрешенное относительно производной. Общее решение этого уравнения имеет вид:
,
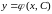(9.6)
где
– произвольная постоянная.
Задача
решения дифференциального уравнения,
которое удовлетворяет начальному
условию:
,
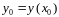имеет название задачи Коши.
Решение дифференциального
уравнения (9.5)
существует не для любой функции
и не при любом начальном условии.
Теорема.
Если в уравнении
функция
и ее частная производная
непрерывны в некоторой замкнутой области
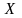и точка
,
то существует единственное решение
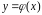этого уравнения, которое удовлетворяет
начальному условию при
.
Геометрический
смысл задачи Коши состоит в том, что
график функции
,
то есть интегральная кривая, которая
проходит через точку
,
единственная.
Если в
точке
условия теоремы Коши выполняются, то
начальное условие
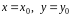будем называть допустимым.
Для
решения задачи Коши в общее решение
уравнения (9.6)
нужно подставить начальное условие и
решить уравнение
относительно постоянной
.
Тогда частное решение
будет решением задачи.
Пример 2. Решить уравнение:
;
.
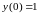Решение. Запишем
уравнение в дифференциалах
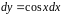и интегрируем его правую и левую части:
.
Используем начальное условие: .
Следовательно,
.
Таким
образом,
является решением задачи Коши.