8) Формули подвійного і половинного аргументу

Із формул додавання отримують формули подвійних кутів шляхом заміни ?=?.

	Примітка: Інколи при перетвореннітригонометричних виразів користуються формулами:  універсальна підстановка

читають сунус двох альфа дорівнює відношенню два тангенс альфа до один плюс тангенс квадрат альфа. Формули половинних кутів ;  ;  . Зауваження Часто використовуються формули пониження степеня: ;  . Вибір знаків "+" або "-" в формулах половинних кутів залежить від того, в якій чверті знаходиться кут  . Зручні для використання формули: 

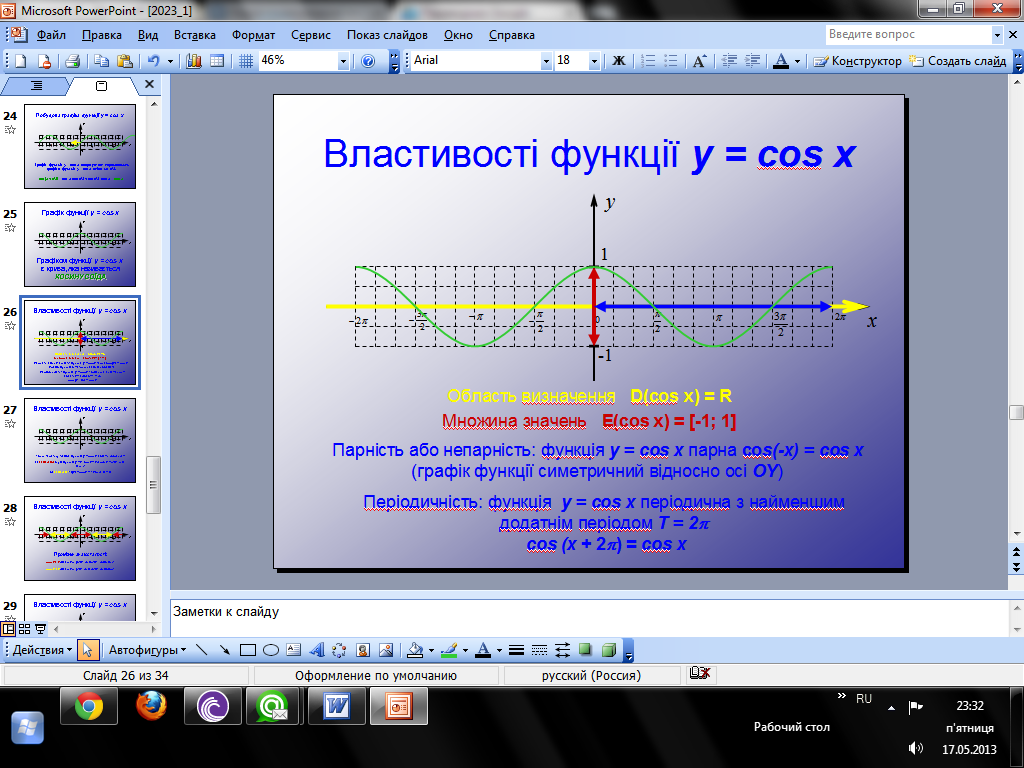
9) Властивості та графіки тригонометричних функцій у = sin x,  у = cosx

10) Властивості та графіки тригонометричних функцій y=tg x, y= ctg x

а) Область визначення: D (CTG х) = R \ {п (п Z)}.

     б) Безліч значень: E (CTG х) = R.

в) Парність, непарність: функція непарна.

     г) Періодичність: функція періодична з основним періодом Т =.

     д) Нулі функції: CTG х = 0 при х = / 2 + N, N Z.

     е) Проміжки знакопостоянства;

;.

      ж) Проміжки монотонності: функція спадає на кожному інтервалі, цілком належить її області визначення.

      з) Екстремуми: ні.

    Графік функції у = х CTG зображений на малюнку.

11) Розв’язки тригонометричних рівнянь sin x=a, cos x= a, tg x= a, ctg x =a

Рівняння називаються тригонометричними, якщо змінна величина знаходиться під знаком тригонометричної функції. Найпростішими тригонометричними рівняннями називаються рівняння виду: sin x=a; cos x=a; tg x=a; ctg x=a. Для їх розв’язку застосовують спеціальні формули:

sin x=a	х=(-1)n 3; ......)2; 1; Z, (k=arcsin a + ?k, k
cos x=a	3; .....)2; 1; Z, (k=arccos a +2 ?k, kx=
tg x=a	3; ......)2; 1; Z, (k=х=arctg a + ?k, k	Ra
ctg x=a	3; ......)2; 1; Z, (k=х=arcctg a + ?k, k	Ra

Приклади розв’язування завдань  Приклад 1 Розв’язати рівняння: 

1)

2)

3) tg x=1;

4) ctg x=

Розв’язання: 1) х=(-1)ⁿ arcsin   + ?k=(-1)ⁿ Z.+ ?k, k 2) arccosx=   +2 ?k=  Z.k 3) х=arctg 1 + ?k=  Z.+ ?k, k 4) х=arcctg   + ?k=  Z.+ ?k,

12. Основні поняття, аксіоми, стереометрії та найпростіші наслідки з них

Нет информации

12. Взаємне розміщення двох прямих у просторі. Теореми про паралельні прямі

Розглянемо деякі співвідношення, які виражають особливості взаємного розташування двох просторових прямих   і  :

• якщо кут між двома прямими  дорівнює  , то

;

• якщо прямі паралельні, то

;

• якщо прямі перпендикулярні, то

• якщо дві прямі знаходяться в одній тій же площині (компланарні), то

• Якщо при цьому  , то прямі, залишаючись компланарними,перетинаються.

• Якщо    ( – некомпланарні), то прямі мимобіжні.

• Якщо прямі зливаються (співпадають), то