Питання до заліку з математики

1.Числова функція. Область визначення і область значення функції. Способи задання функції

В математики числова функція - це функція, області визначення і значень якої є підмножинами числових множин - як правило, безлічі дійсних чисел   або безлічі комплексних чисел   .

Числовою функцією з областю визначення Dназивається відповідність, при якої кожному числу x з множини D співставляється за деяким правилом число y, що залежить від x.

Функція - залежність змінної у від змінної x, при якій кожному значенню х відповідає єдине значення у.     Змінна х - незалежна змінна або аргумент.     Змінна у - залежна змінна

Значення функції - значення у, що відповідає заданому значенню х

Область визначення функції - усі значення, яких набуває незалежна змінна.

Область значень функції (множина значень) - усі значення, яких набуває функція.

 Функція є парною - якщо для будь-якого х з області визначення функції виконується рівність f(x)=f(-x)     Функція є непарною - якщо для будь-якого х з області визначення функції виконується рівність f(-x)=-f(x)     Зростаюча функція - якщо для будь-яких х1 і х2, таких, що х1< х2, виконується нерівність f(х1)<f(х2)     Спадна функція - якщо для будь-яких х1 і х2, таких, що х1< х2, виконується нерівність f(х1)>f(х2)

Способи завдання функції

Якщо зі зміною однієї величини зміниться й інша, то ми маємо справу з функціональною залежністю, функціональну залежність можна задавати формулами, графіками, таблицями. • Щоб задати функцію, потрібно вказати спосіб, за допомогою якого для кожного значення аргументу можна знайти відповідне значення функції. Найбільш уживаним є спосіб завдання функції за допомогою формули у=f(x), де f(x)-вираз, що містить змінну х. У такому випадку говорять, що функція задана формулою або що функція задана аналітично. • На практиці часто використовується табличний спосіб завдання функції. При цьому способі приводиться таблиця, що вказує значення функції для наявних у таблиці значень аргументу. Прикладами табличного завдання функції є таблиця квадратів, таблиця кубів, таблиця температур.     Найчастіше функцію задають за допомогою формули. При цьому якщо не дано додаткових обмежень, то областю визначення функції, заданою формулою, вважають множину усіх значень змінної, при яких ця формула має сенс.    Наприклад, формула f(x)=1/x має сенс при всіх x ≠ 0, тому областю визначення функції f(x) = 1/x вважають множину усіх не рівних нулю дійсних чисел. Область її значень збігається з областю визначення і є об'єднанням інтервалів (–∞; 0) і (0; ∞).   Область визначення функції y = tg x — об'єднання всіх інтервалів виду де n ; область її значень — уся числова пряма, тобто E(tgх) = (–∞; ∞).

2. Графік функції. Найпростіші перетворення графіків функції

Графіком функції   називається підмножина декартового добутку   на  ( ), що містить всі пари (x, y), для яких f(x)=y.

Якщо простіше, то це є малюнок, на якому можна побачити як змінюється значення Y в залежності від значення Х. Як правило, значення X позначають на горизонтальній прямій, яку називають віссю абсцис (x), а значення Y на перпендикулярній до неї прямій, яку називають віссю ординат (y). Ці осі разом утворюють систему координат. Кожна вісь має напрямок, у якому значення відповідної координати зростає. У точці найбільшого значення малюють стрілку, яка вказує цей напрям. На кожній осі роблять позначки окремих (ключових) значень і підписують їх цими значеннями. Це допомагає приблизно визначити інші проміжні значення. Точка з координатами x=0 і y=0 називається початком координат.

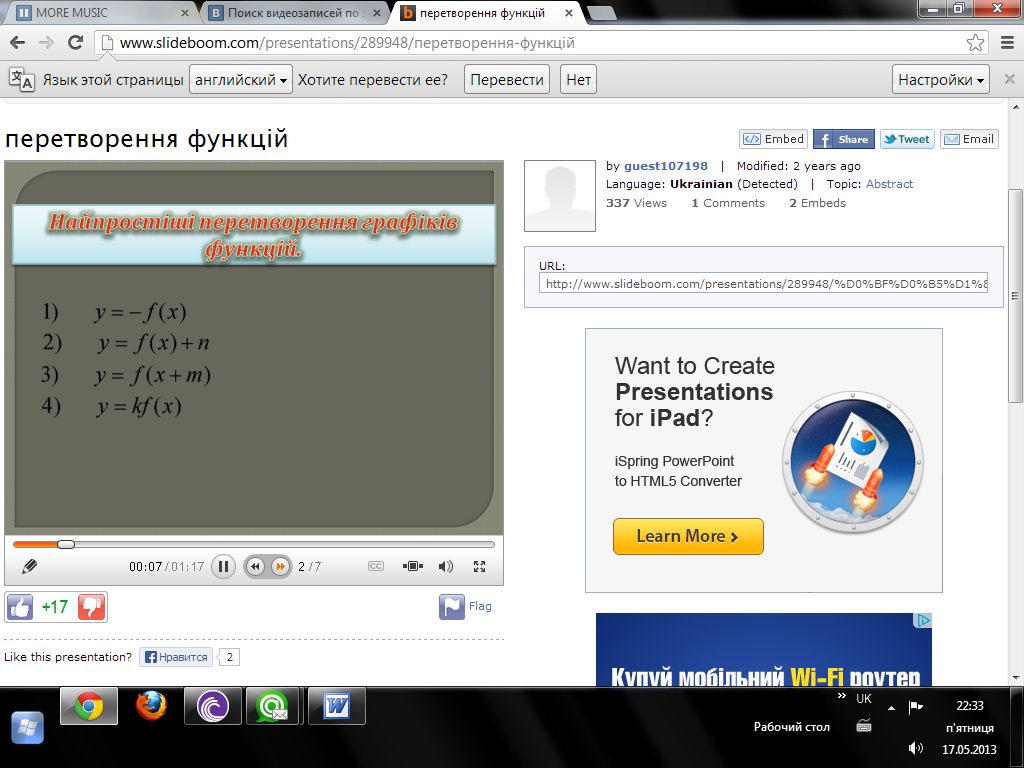
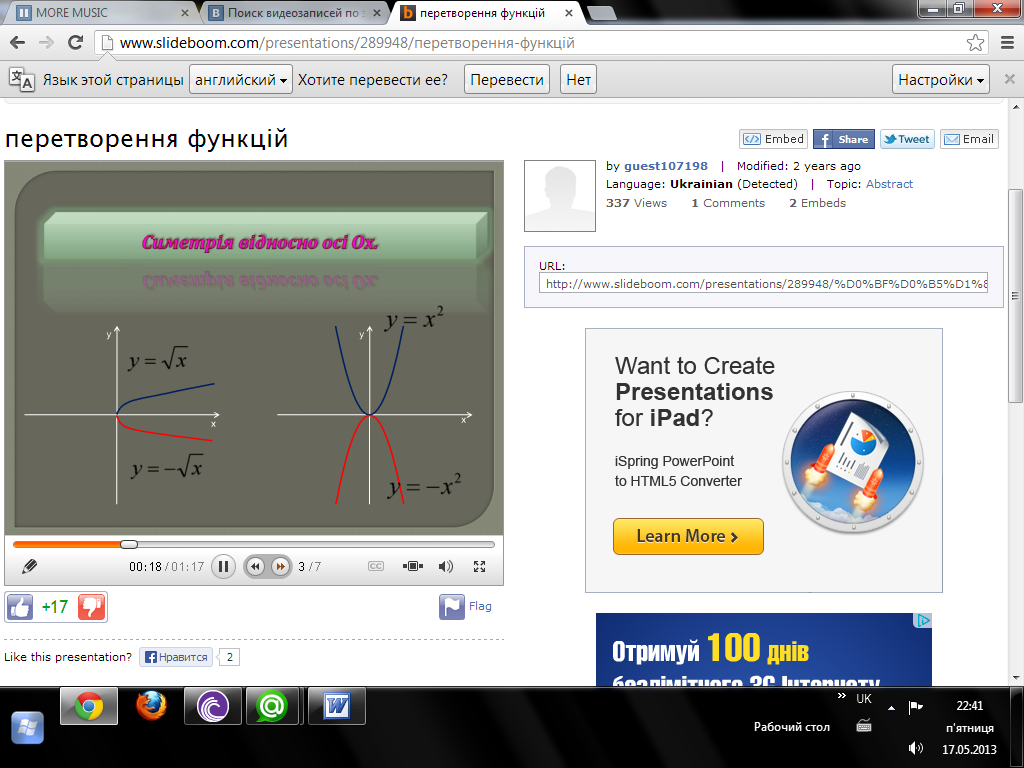
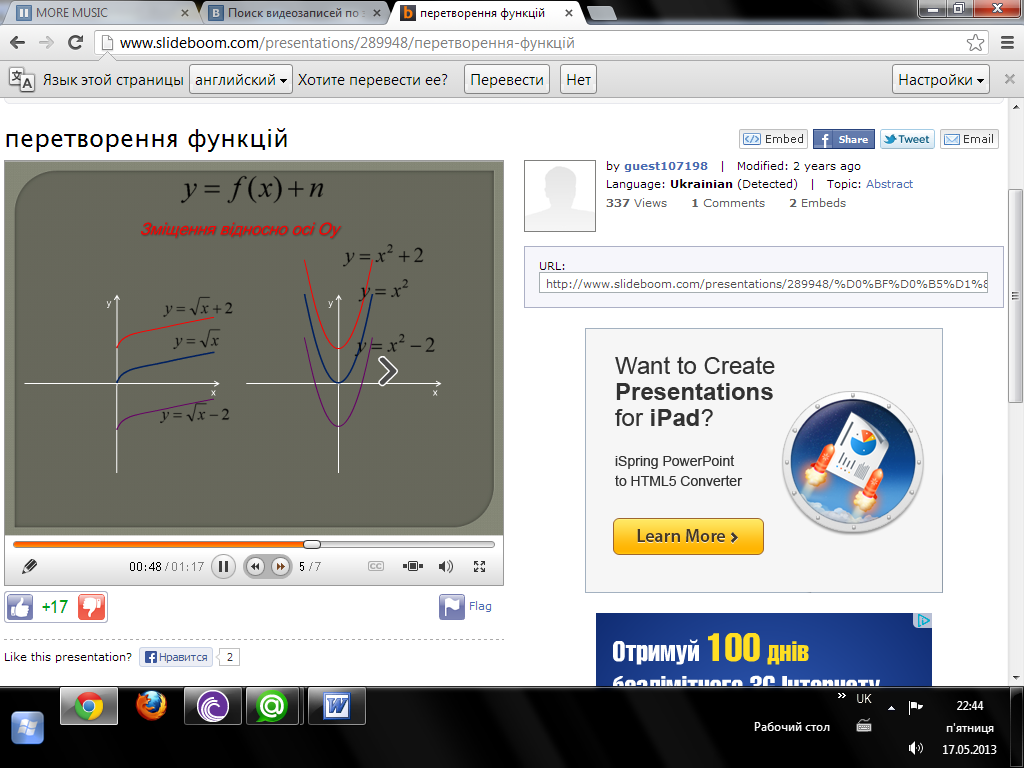
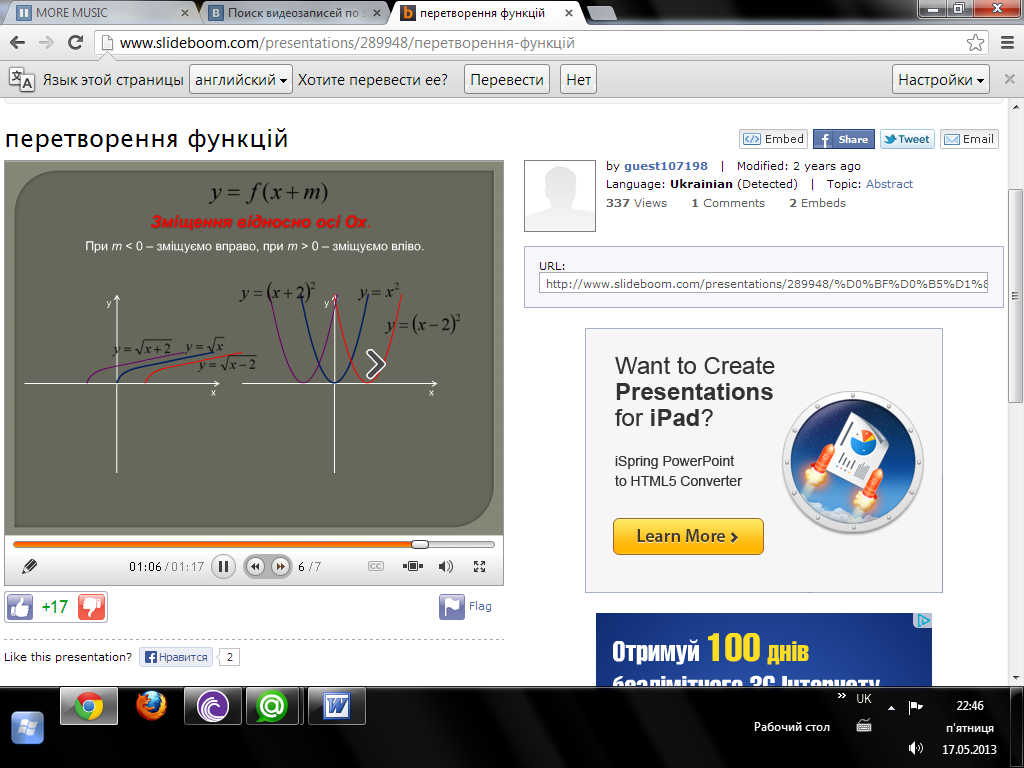
Найпростіші перетворення графіків функцій