Екзаменаційний білет n 19.

1. Дискретний двовимірний розподіл ймовірностей та відповідні одновимірні розподіли.

2. Числові характеристики випадкової величини з біноміальним розподілом ймовірностей.

Функція неперервного розподілу статистичних ймовірностей має вигляд

Знайти математичне сподівання випадкової величини .

Екзаменаційний білет n 20

1. Умовні статистичні ймовірності. Статистична ймовірність добутку подій. Формула повної статистичної ймовірності.

2. Нерівність Чебишова та її застосування.

3. . Знайти , використовуючи формулу , де , – щільність рівномірного розподілу ймовірностей на множині . Дати відповідні геометричні тлумачення. Екзаменаційний білет n 21.

1. Повторні незалежні випробовування.Формула Бернуллі

2. Функція розподілу ймовірностей випадкового вектора X є та її властивості.

3. При передаванні телеграфних повідомлень за допомогою двох знаків " " і " – " статистична ймовірність появи знака "–" в кодах повідомлень дорівнює 0,55, а знака " " – 0,45. При цьому знак "–" спотворювався з статистичною ймовірністю 0,10, а знак " " – з статистичною ймовірністю 0,15. Чому дорівнює статистична ймовірність появи знака "–" в кодах прийнятих повідомлень?

Екзаменаційний білет n 22.

1. Випадкові величини. Операції над випадковими величинами.

2. Математичне сподівання випадкової величини та його властивості.

3. . Знайти , використовуючи формулу , де , – щільність рівномірного розподілу ймовірностей на множині . Дати відповідні геометричні тлумачення.

Екзаменаційний білет n 23.

1. Повторні незалежні випробування, формула Бернуллі.

2. Математичне сподівання випадкової величини та його властивості.

3. Пакувальник складає 2100 деталей. Ймовірність того, що деталь мічена, дорівнює 0,15. Що більш ймовірно, що в пакунку виявиться від 200 до 235 мічених деталей, чи від 720 до 755?

Екзаменаційний білет n 24.

1. Умовні ймовірності. Залежні і незалежні випадкові події. Формула повної ймовірності. Формула Байєса.

2. Моменти випадкових величин та їх властивості. Приклади.

3. Фільмокопії виготовляють на трьох кінофабриках. Продуктивність першої фабрики в 5 разів більша, ніж другої, а продуктивність третьої в 6 разів менша, ніж першої. Ймовірності виготовлення на кожній фабриці стандартної фільмокопії відповідно дорівнюють 0,9, 0,95, 0,85. Одержана фільмокопія виявилась нестандартною. Яка ймовірність того, що її виготовлено на другій фабриці.

Екзаменаційний білет n 25.

1. Закон великих чисел. Теореми Чебишова і Бернуллі.

2. Розподіли ймовірностей складових двовимірного випадкового вектора. Залежні і незалежні випадкові величини.

3. За даним розподілом абсолютних частот побудувати гістограму та графік функції розподілу статистичних ймовірностей:

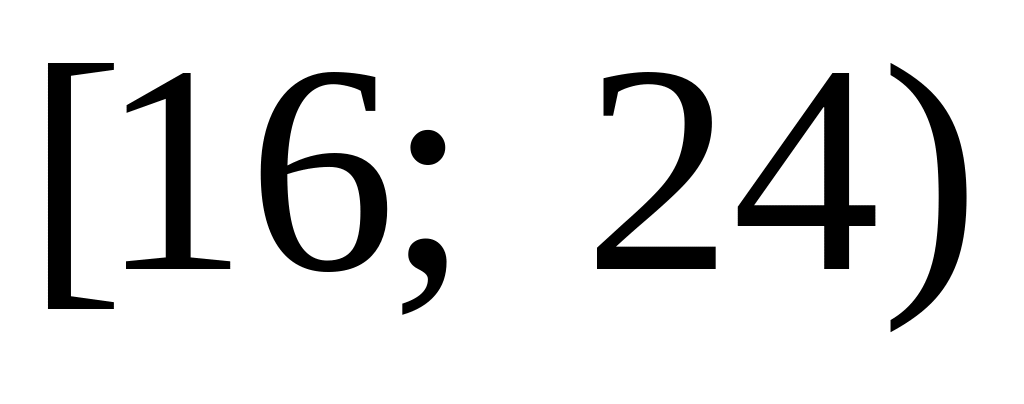
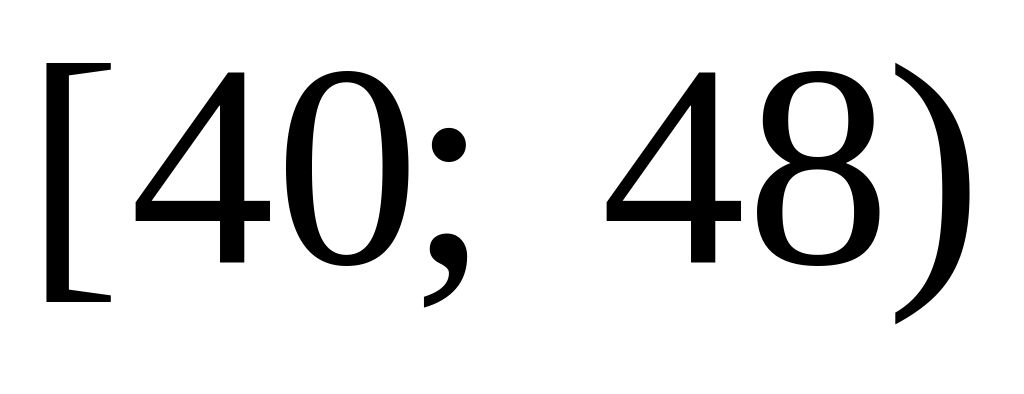
	10	15	20	25	20	10

за допомогою програми Gran1.