1. Алгебра множеств, свойства операций объединения, пересечения и дополнения.

Множество– совокупность объектов, хорошо различимых нашей интуицией или мыслью, обладающих неким сходством и объединенных в одно общее.

Основные понятия:

• Мощность множества( )– количество элементов в множестве.

• Два множества равны ( ), если состоят из одних и тех же элементов.

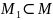• _­ подмножество ( ), если для , в то же время надмножество .

• Булеанмножества M ( )– множество всех подмножеств множества M

• Пустоемножество ( 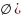– множество, в состав которого не входит ни одного элемента.

• Универсум ( )– множество, включающее все возможные элементы.

Алгебройназывается пара , где:

• – носитель, множество элементов какой-либо природы.

• – сигнатура, конечный набор операций над множеством.

Алгеброй множеств(или Канторовой алгеброй) называется алгебра , где:

• Операция объединения: .

• Операция пересечения: .

• Операция дополнение до универсума: .

Свойства операций:

• Идемпотентность:

  • 

  • 

• Коммутативность:

  • 

  • 

• Ассоциативность:

  • 

  • 

• Дистрибутивность:

  • 

  • 

• Закон де Моргана:

  • ;

  • .

• Закон двойного дополнения:

• Свойства универсума:

  • 

  • 

  • 

• Свойства пустого множества:

  • 

  • 

  • 

2. Бинарное отношение. Операции над отношениями. Обратное и дополнительные отношения. Композиция отношений. Ядро отношения.

Декартово произведение двух множеств – это множество пар .

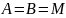Бинарное отношение двух множеств и - этонекоторое подмножество из декартового произведения: Если , то называется бинарным отношением на .

Способы задания отношений:

• Прямое перечисление:

• 	a	b	c
  a	1	1	0
  b	0	0	1
  c	0	0	0

  Матрица смежности:

• Графически на ориентированном графе :

  ; .

• Функциональный:

.

Операции над отношениями:

• Операция объединения:

• Операция пересечения: .

• Операция обращения:

• Операция дополнения:

• Операция композиции:

Ядром отношения называется его композиция с обратным, т.е. .

Пример.

.

.

.

.

.

.

.

.

3. Свойства бинарных отношений. Рефлексивность, симметричность, транзитивность, иррефлексивность, антисимметричность, интранзитивность.

Отношение R:

• рефлексивно, если .

  • наличие петель у всех вершин;

  • все единицы на главной диагонали.

• иррефлексивно, если

  • отсутствие петель у всех вершин;

  • отсутствие единиц на главной диагонали.

• нерефлексивно, если оно ни рефлексивно, ни иррефлексивно.

  • не у всех вершин есть петли, но есть хотя бы у одной;

  • на главной диагонали есть единицы, но не на всей.

1 2 3 4 1 1 1 2 1 1 1 3 1 1 4 1 1 2 3 4 1 1 1 2 1 1 3 1 4 1 2 3 4 1 1 1 1 2 1 1 1 3 1 4

• симметрично, если

  • все дуги, кроме рефлексивных, парны;

  • матрица симметрична.

• антисимметрично, если

  • ни одна дуга, кроме рефлексивной, не имеет пару;

  • матрица антисимметрична.

• асимметрично,если , т.е. антисимметрично и иррефлексивно.

  • ни одна дуга не имеет пару и рефлексивных дуг нет;

  • матрица антисимметрична без единиц на главной диагонали.

• несимметрично, если оно ни симметрично, ни антисимметрично.

  • не все дуги парны;

  • несимметричная матрица, у которой хотя бы одна ячейка имеет симметричную.

1 2 3 4 1 1 2 1 1 1 3 1 1 4 1

1 2 3 4 1 1 2 1 1 1 3 1 4

1 2 3 4 1 1 2 1 1 3 1 4

1 2 3 4 1 1 1 2 1 1 3 1 4

• транзитивно, если

  • все цепочки из двух последовательных дуг должны иметь рефлексивное замыкание;

  • может использоваться алгоритм Флойда-Уоршалла.

• интранзитивно, если

  • все цепочки из двух последовательных дуг не должны иметь рефлексивного замыкания;

  • может использоваться алгоритм Флойда-Уоршалла.

• нетранзитивно, если оно ни транзитивно, ни интранзитивно.

  • ряд цепочек содержит рефлексивные замыкания, а ряд нет.

  • может использоваться алгоритм Флойда-Уоршалла.

1 2 3 4 1 1 1 1 2 1 3 1 1 4 1 1 2 3 4 1 1 2 1 1 3 1 4 1 2 3 4 1 2 1 1 3 1 1 4 1 1