5.Градиент скалярного поля.
Пусть
на множестве
задана функция
и в каждой точке множества
существуют все частные производные
функции
.
Определение.
Градиентом функции
в точке
называют вектор, координатами которого
являются значения частных производных
функции
в этой точке. Этот вектор обозначается
Таким
образом,
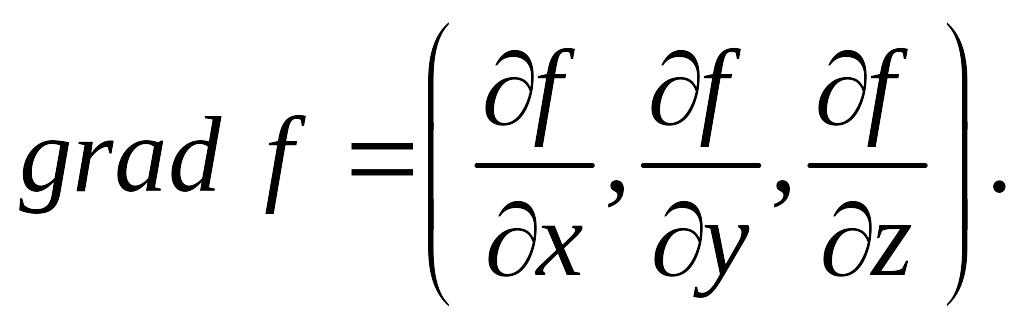
Говорят,
что на множестве
определено поле градиента, если в каждой
точке
определен вектор
Замечание.
Градиентом
функции двух переменных
называется вектор
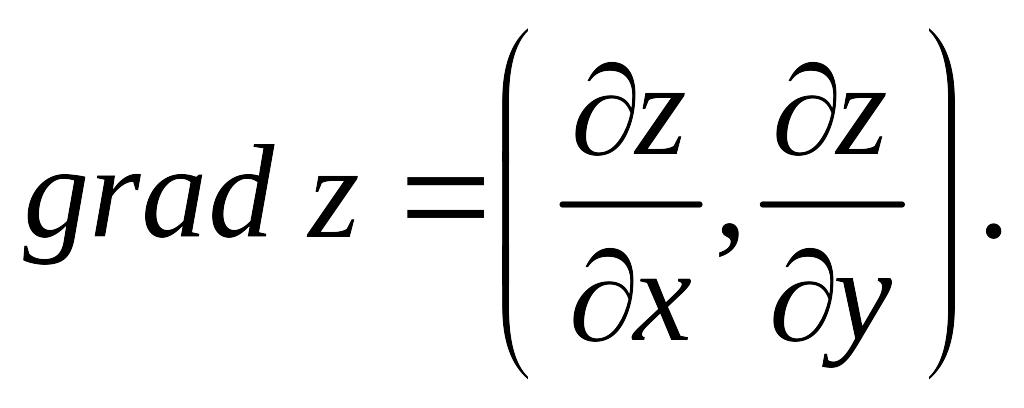
Отметим без доказательства важное свойство градиента:
Градиент
функции
(или
)
в точке
,
то есть вектор
,
перпендикулярен линии уровня (поверхности
уровня), проходящей через
,
и направлен в сторону максимального
увеличения функции.
6. Касательная плоскость к поверхности.
В качестве одного из приложений дифференциального исчисления функций многих переменных рассмотрим задачу о касательной плоскости к поверхности.
Теорема
1.
Пусть поверхность
является графиком функции
и функция
имеет непрерывные частные производные
в
,
где
и
Тогда в точке
существует касательная плоскость к
поверхности
,
которая задается уравнением
где
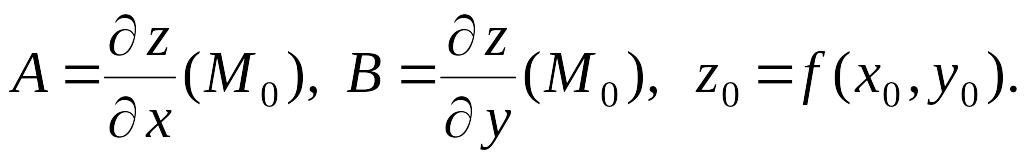
Теорема
2. Пусть
поверхность
задана уравнением
и точка
,
то есть
Пусть также
имеет непрерывные частные производные
в
,
где
и
Тогда в точке
существует касательная плоскость к
поверхности
,
которая задается уравнением
,
где
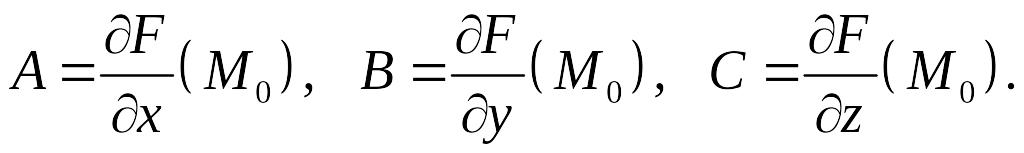
Пример. Найти уравнение касательной плоскости к поверхности
в
точке
Решение.
Вычислим
частные производные в точке
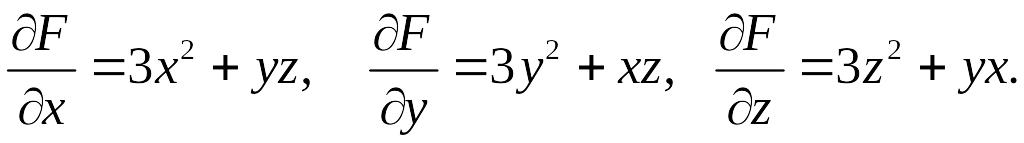
Тогда в соответствии с теоремой 2 находим
Уравнение касательной плоскости имеет вид
или
.
7. Экстремумы функций многих переменных.
Пусть
задана функция
,
где
и пусть
Определение. Точка называется точкой локального максимума (минимума) для функции , если существует такое, что
Точки локального максимума или минимума называют точками экстремума.
Определение.
Точка
называется критической точкой функции
если в этой точке все частные производные
существуют и равны 0, то есть
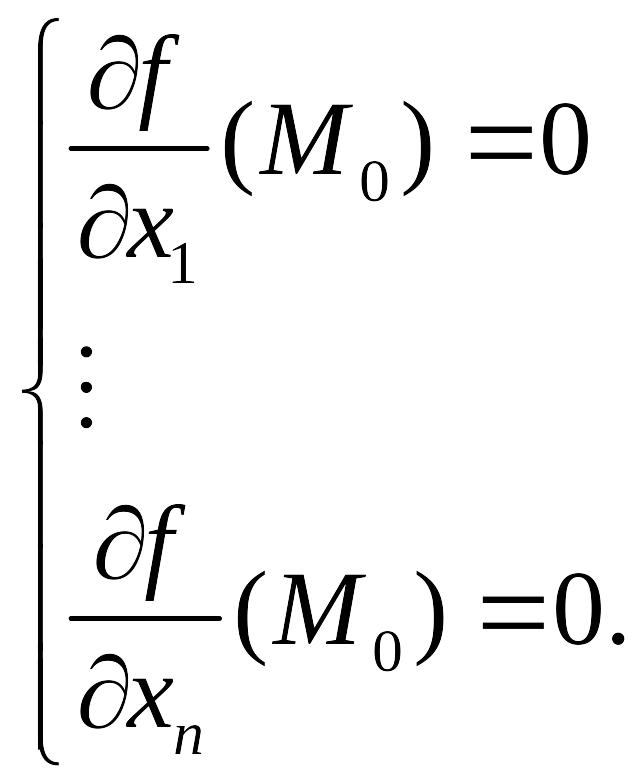
Следствием известной теоремы Ферма для функции одной переменной является следующая теорема, которая устанавливает связь между критическими точками и экстремумами.
Теорема 1. Если точка является точкой экстремума функции и в этой точке у f существуют все частные производные, то точка - критическая для .
Данная теорема называется необходимым условием экстремума.
Отметим, что также, как и для функций одной переменной, необходимое условие не является достаточным для существования экстремума.
Например,
очевидно, что точка
является критической точкой для функции
.
Однако, эта точка не является ни точкой локального максимума ни точкой локального минимума.
Задача.
Доказать, что точка
не является точкой экстремума функции
Указание.
Для любого
в
функция
принимает положительные и отрицательные
значения.
Из
теоремы 1 следует, что если в каждой
точке
существует
,
то экстремумы следует искать среди
критических точек
.
Сформулируем без доказательства достаточные условия экстремума функции двух переменных:
Теорема 2. Пусть все вторые частные производные функции непрерывны в , где и . Пусть является критической точкой для , то есть
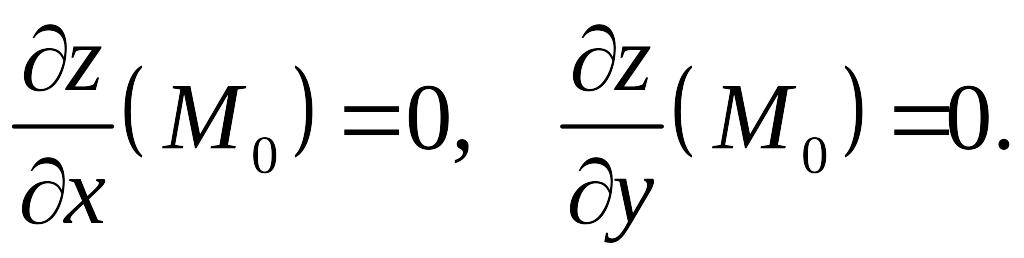
Обозначим
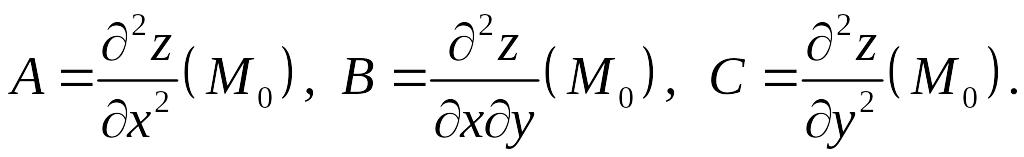Тогда
если
,
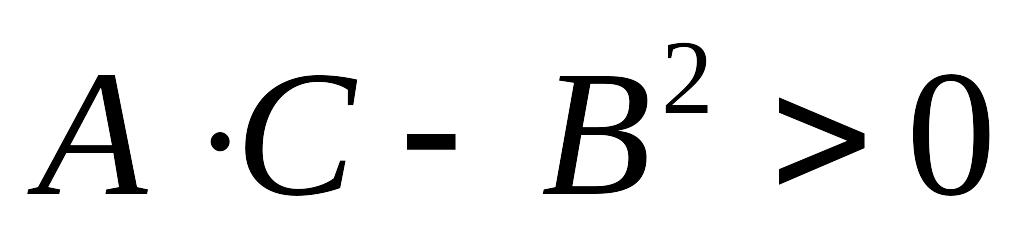то
точка экстремума
,
причем при
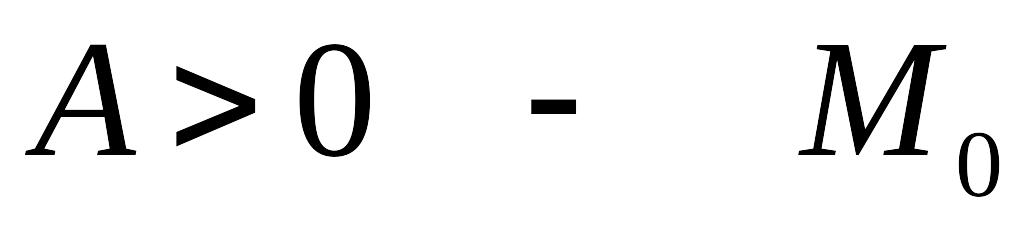точка локального минимума, а при
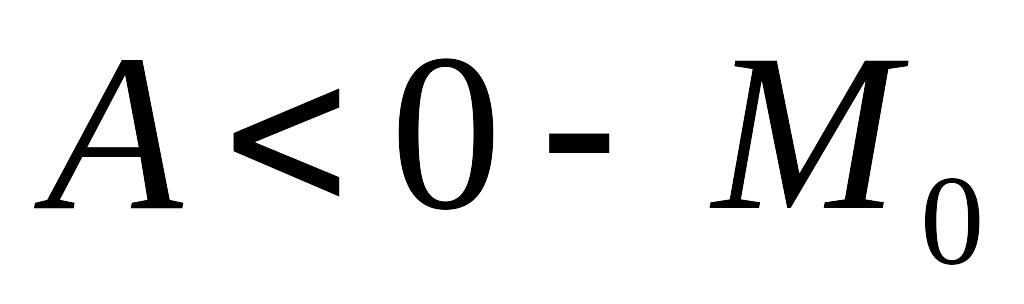точка локального максимума.
если
,
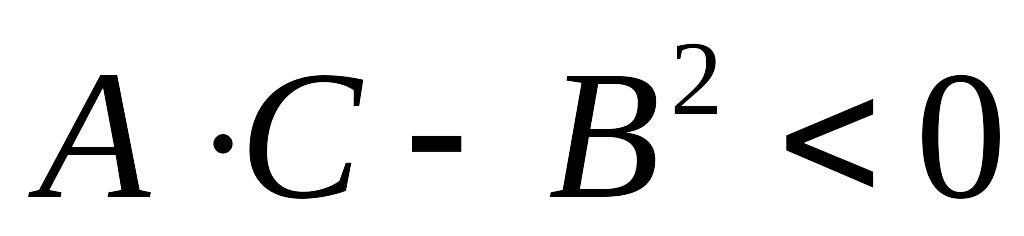то
не является точкой экстремума.
Замечание.
Из теорем 1, 2 следует такой план отыскания
точек экстремума функций двух переменных
,
имеющей непрерывные частные производные
второго порядка в
Найти критические точки .
В критических точках проверить достаточные условия экстремума, то есть условия теоремы 2.
Пример.
Исследовать
функцию
на экстремумы.
Решение.
Найдем частные производные
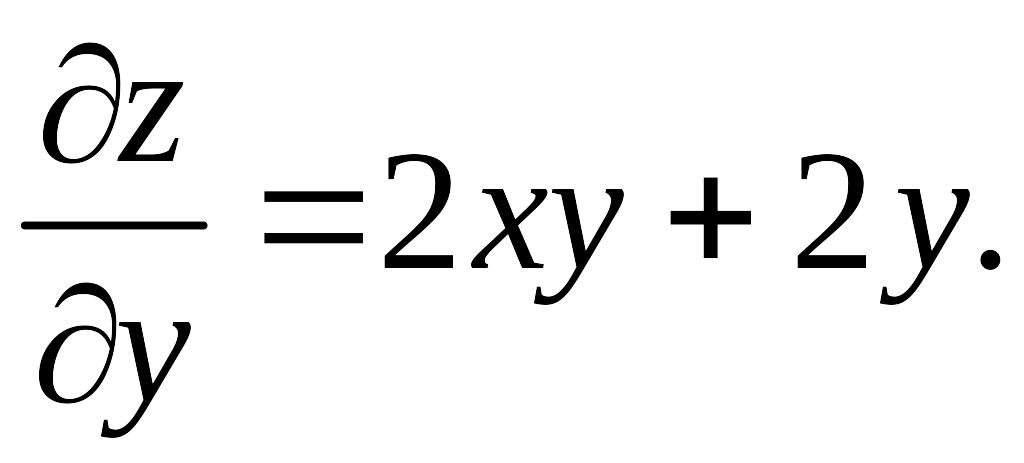
Для отыскания критических точек составим систему
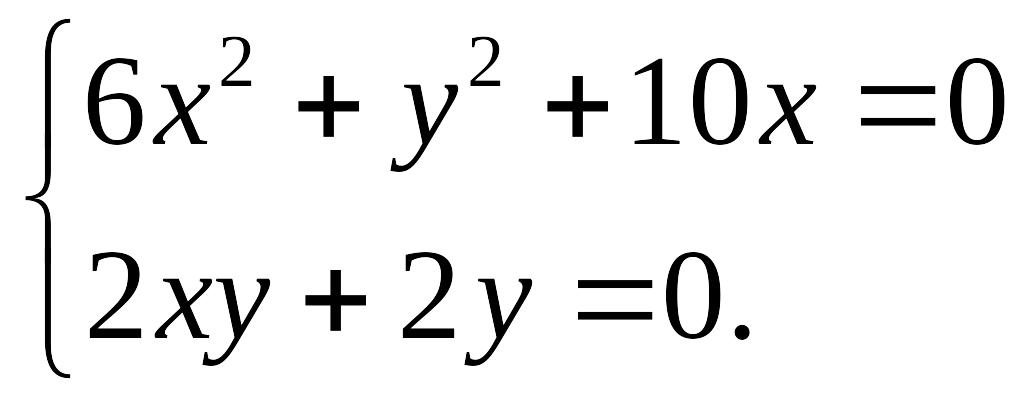
Решив систему, получим четыре критических точки
2)
В точках
проверим условия теоремы 2. Для этого
найдем вторые частные производные:
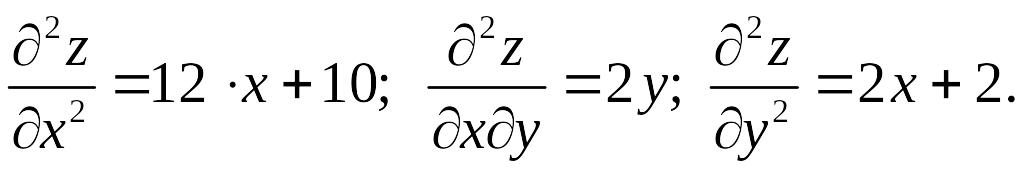
В
точке
имеем
Поэтому
А так как
точка
-
точка локального минимума.
В
точке
имеем
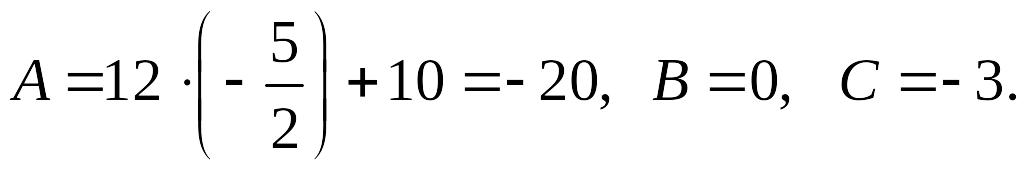
Тогда
и
Поэтому
точка локального максимума.
В
точке
находим
В точке
также
,
поскольку
Поэтому
не являются точками экстремума.
Ответ: точка локального минимума,
точка локального максимума.