2.Тригонометрические подстановки.

Определение. Будем обозначать R(x, y) такую функцию, которая получается их x, y и некоторых постоянных с помощью арифметических операций +, -, , : . Такая функция называется рациональной функцией от своих аргументов.

Пример.

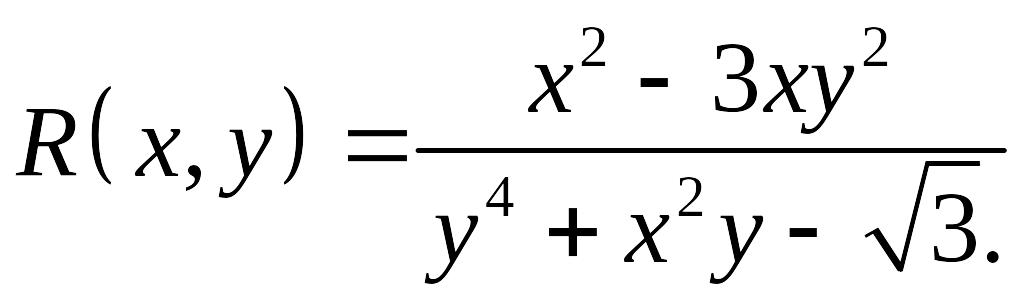
В этом и следующих пунктах при вычислении интегралов будут предложены подстановки, которые приводят к интегралам от рациональных дробей.

Определение. Проведение такой подстановки называется рационализацией интеграла.

Рассмотрим интегралы вида

(9)

где R(u,v)- рациональная функция. Рационализация этого интеграла достигается с помощью подстановки:

, при (10)

Для проведения подстановки (10) выразим

(11)

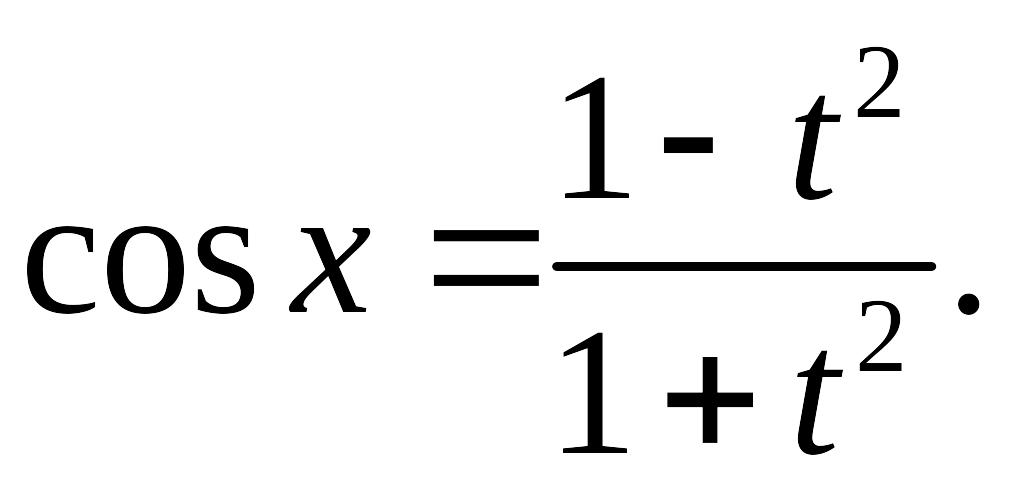(12)

Из (10) – (12) и (8) следует:

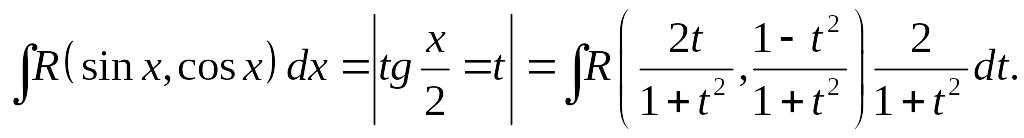
Так как R (u,v) - рациональная функция, то под знаком интеграла получена рациональная дробь.

Определение. Подстановка (10) называется универсальной.

Пример.

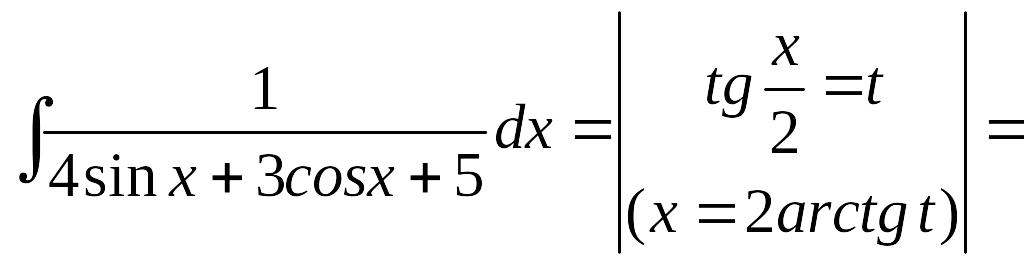
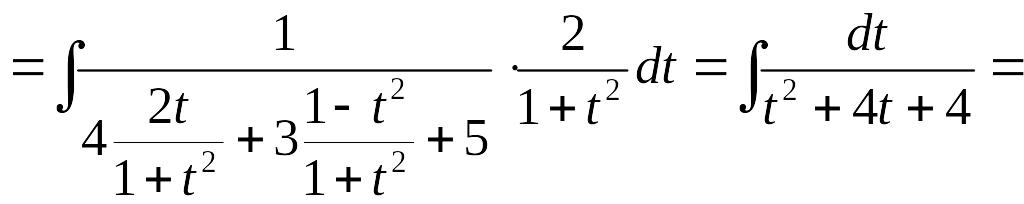
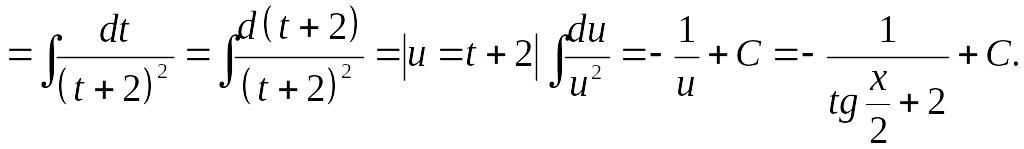
Замечание. Универсальная подстановка часто приводит к громоздким вычислениям. Если подынтегральная функция R(u,v) обладает некоторыми симметричными свойствами, то быстрее к цели приводит одна из следующих подстановок:

1. Если , то применяется подстановка:

.

2. Если , то применяется подстановка:

.

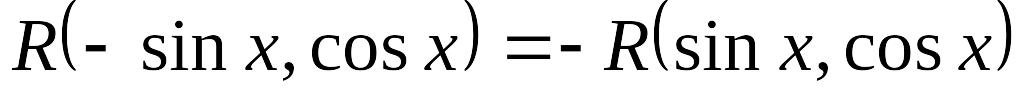
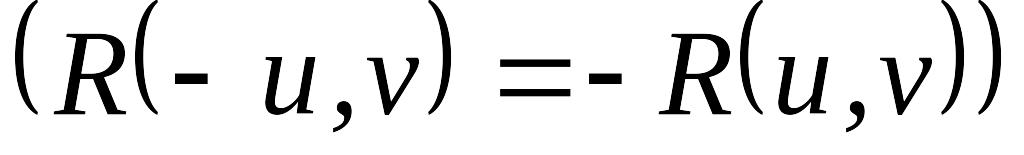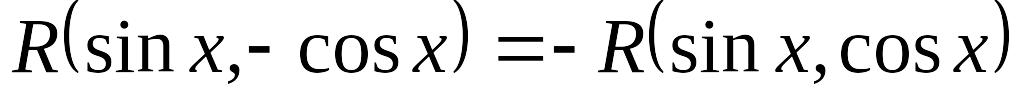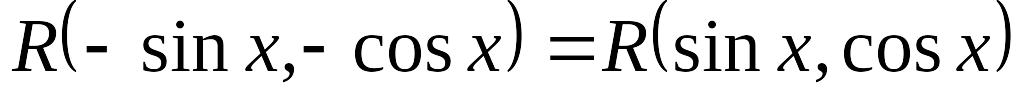3. Если , то применяется подстановка:

при .

3. Интегрирование иррациональных функций.

Рассмотрим интеграл вида

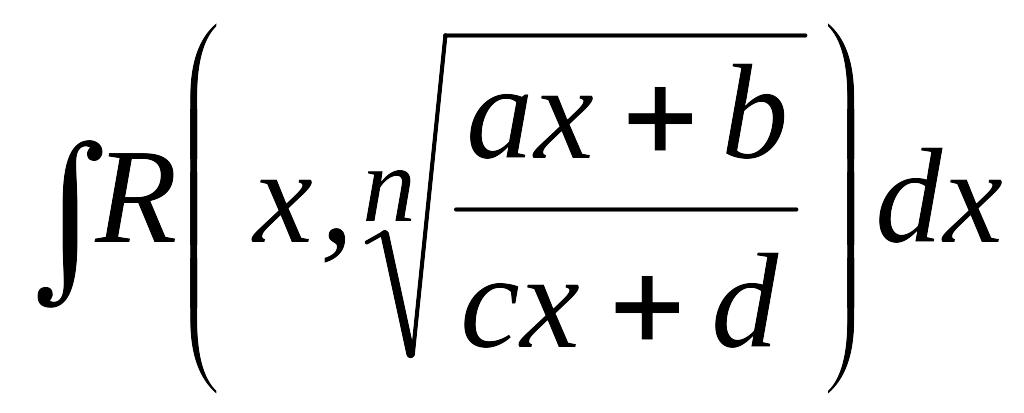, (13)

где R – рациональная функция и .

Интеграл (13) рационализируется подстановкой: . Выразим из этого равенства x:

; ; ;

; .

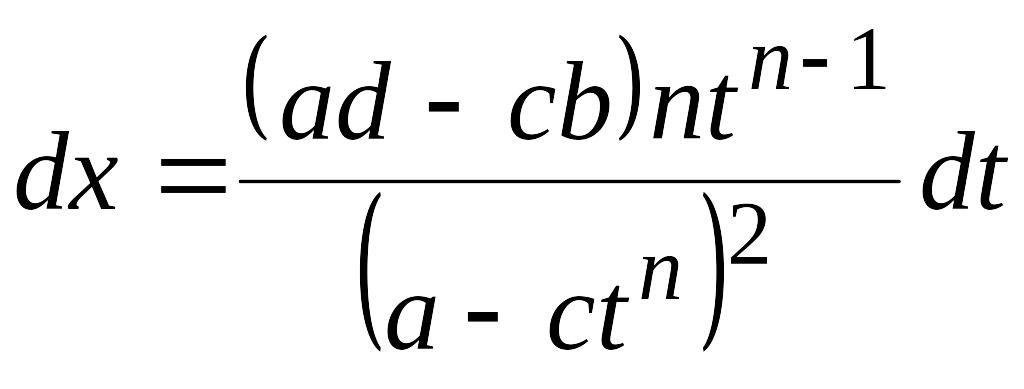Пример.

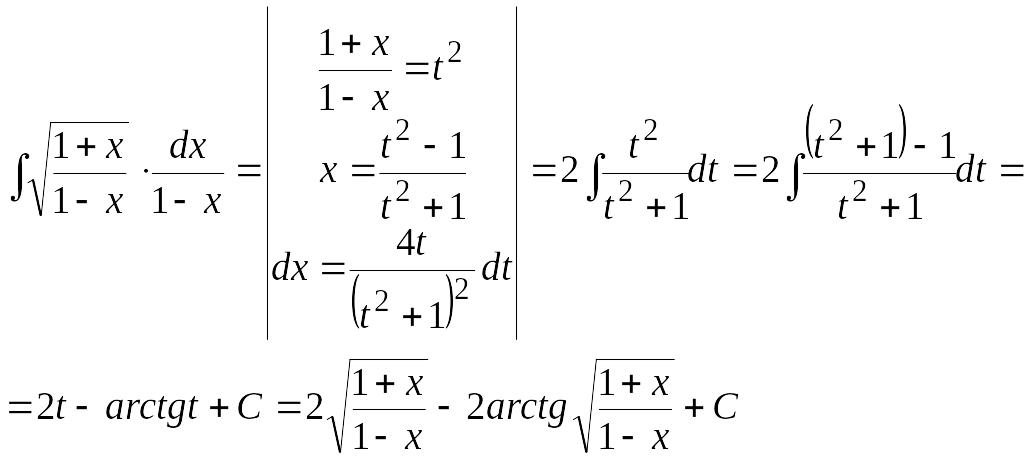
4. Подстановка Эйлера.

Рассмотрим интеграл вида

. (14)

Здесь . Обозначим . Возможны следующие случаи:

1 случай. D > 0. Обозначим через x₁, x₂ корни уравнения . Тогда

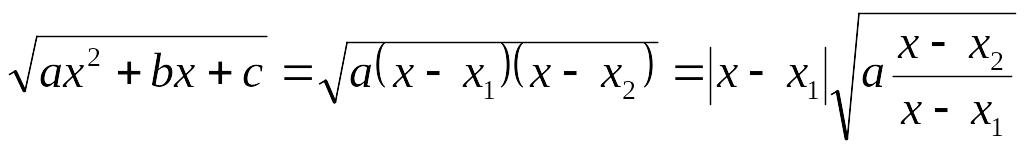
и согласно пункта 3 подстановка рационализирует интеграл (14). При этом модуль раскрывается на соответствующем промежутке.

2 случай. D < 0. Тогда a > 0. Рассмотрим подстановку

. (15)

Выразим отсюда x: ;

; .

Следовательно, подстановка (15) рационализирует интеграл (14). Подстановка (15) называется подстановкой Эйлера.

Замечание. Подстановка (15) рационализирует интеграл (14) и в случае, когда D > 0 и a > 0.

3 случай. D = 0. В этом случае под знаком корня находится полный квадрат. Поэтому подынтегральная функция преобразуется в многочлен или рациональную дробь.

Замечание. При вычислении интегралов

I. , II. , III. .

можно применить подстановки из пунктов 3, 4. От корня в подынтегральной функции в интегралах I, II, III можно избавиться также с помощью следующих тригонометрических подстановок:

I. ( );

II. ;

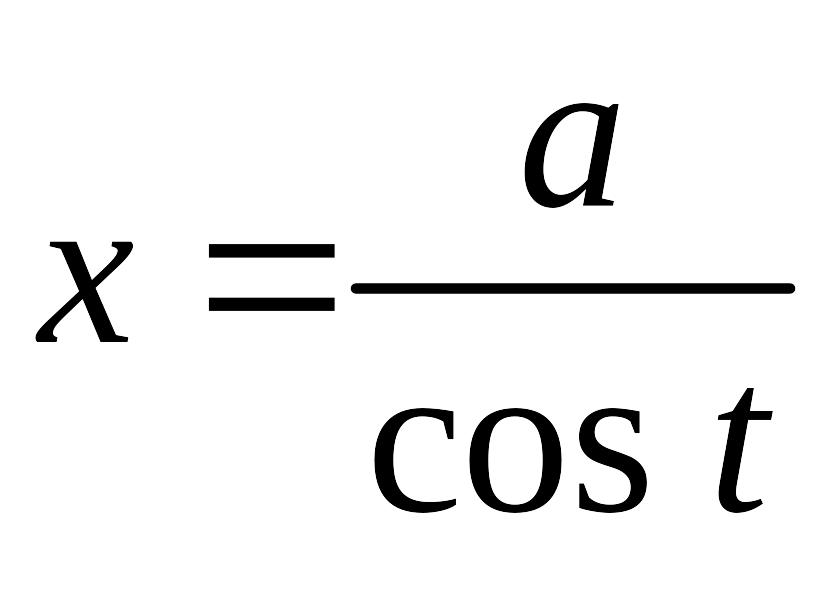III. .

Пример. Найти интеграл

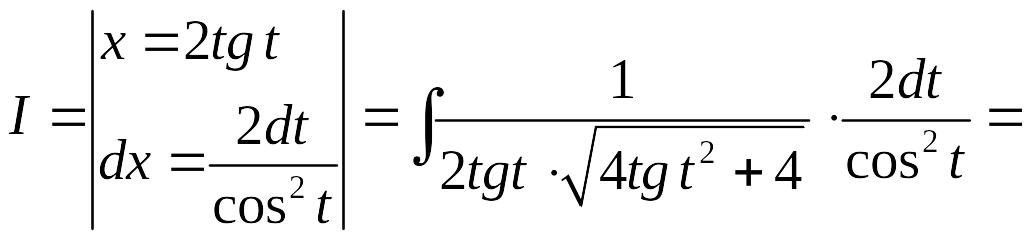
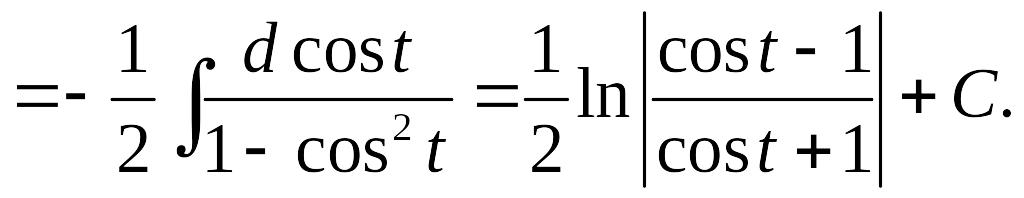
Так как то 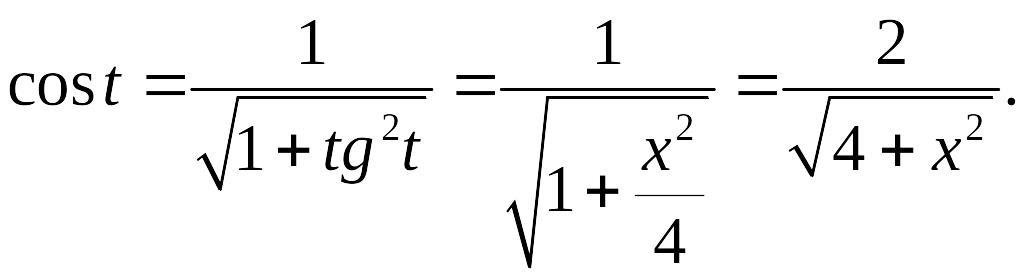Поэтому

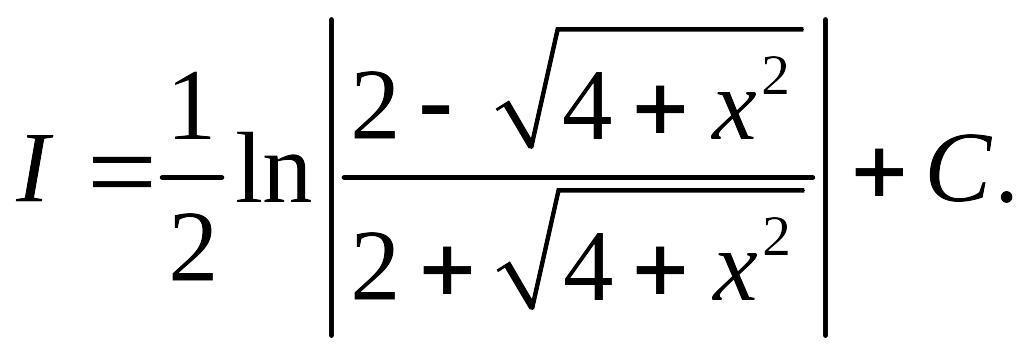
Замечание. Интеграл (14) можно привести к виду I, II, III, если под знаком корня выделить полный квадрат и ввести новую переменную