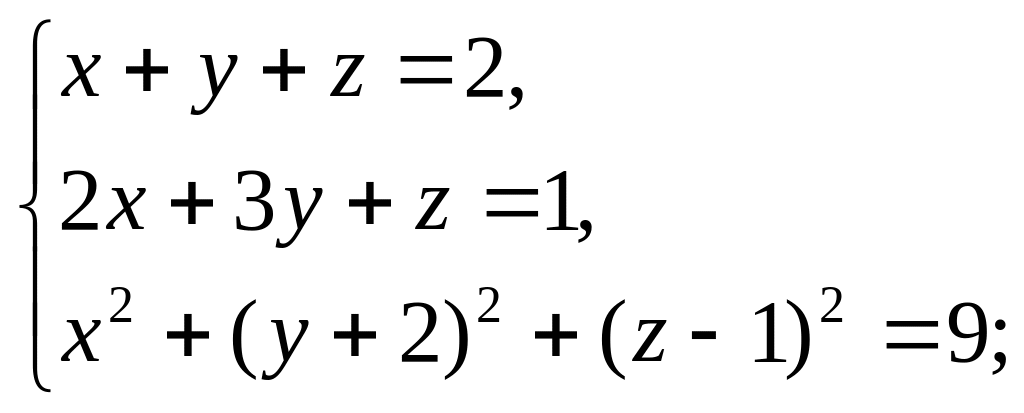2.3. Решение систем уравнений

Пример 1. Решить систему уравнений

Решение. Составляем функцию и ищем значения х, у, при которых z = 0.

1. В ячейку С1 вводим функцию z, заменяя х на а1, у на b1.

2. Открываем диалоговое окно Поиск решения и задаем сценарий решения, как показано на (рис. 2.27).

Рис. 2.27

3. По команде Выполнить получаем (рис. 2.28) результаты поиска решения.

Рис. 2.28

4. Проверкой (рис. 2.29) убеждаемся, что (7; 3) решение системы.

Рис. 2.29

Изменяем формулу ячейки С1, удаляем содержимое ячеек А1 и В1 и снова применяем настройку Поиск решения, что дает рис. 2.30.

Рис.2.30

6. Проверкой убеждаемся, что (–7; –3) также решение системы. Дальнейшее применение надстройки Поиск решения показывает, что других решений система не имеет.

Ответ: (7; 3), (–7, –3).

Задания для самостоятельной работы

1. Решить системы уравнений:

а)	б)	в)
г)	д)	е)
ж)	з)	и)

2.4. Построение графиков с помощью мастера диаграмм

С помощью Мастера диаграмм график функции y = f (x) строится по выделенной таблице значений независимой переменной и функции, тип диаграммы: точечная.

Пример 1. Построение кривой, заданной в полярных координатах.

Построить кардиоиду

Решение.

1. Последовательность значений  зададим как арифметическую прогрессию с шагом h = 0,314 и первым членом а₁ = 0. Для этого выполним следующие действия.

а) Введем в ячейку А1 значение 0;

б) Командами Правка  Заполнить  Прогрессия откроем диалоговое окно Прогрессия и заполним его поля, как на рис. 2.31;

в) После нажатия ОК появляется столбец значений переменной  .

Рис. 2.31

2. В ячейку В1 вводим формулу = cos(a1) + 1 и методом «протаскивания» заполняем столбец значений функции.

3. Выделяем столбец значений функции и открываем диалоговое окно Мастер диаграмм. Устанавливаем тип диаграммы: Лепестковая. Выполнив все необходимые шаги, приходим к графику (рис. 2.32).

Рис. 2.32

Пример 2. Построение поверхности.

Построить параболоид вращения z= x² + y² , x  [–1, 1], y  [–1, 1], h = 0,1.

Решение. Построение поверхности z = f(x, y), x  [a, b], y  [c, d] начинается с задания таблицы значений функции f(x, y) в узлах прямоугольной сетки, соответствующих заданным (выбранным) шагам h_x, h_y. Далее оно проводится пошаговым графическим редактором Мастер диаграмм, тип диаграммы – поверхность.

1. В ячейку А2 вводим значение –1, а в ячейку А3 – значение –0,9. Выделяем обе ячейки и методом «протаскивания» заполняем диапазон А2:А22 значений переменной х.

2. Аналогично в ячейку В1 вводим значение –1, а в ячейку С1 – значение –0,9 и заполняем диапазон В1:V1 значений другой переменной.

3. В ячейке В2, учитывая, что значения независимых переменных х, у должны браться из первого столбца и первой строки соответственно, т.е. ссылки на первый столбец и первую строку должны быть абсолютными, задаем формулу $A2^2+B$1^2.

4. Берем «мышью» маркер заполнения рамки ячейки В2 и, «протаскивая» его до ячейки V22, копируем формулу ячейки В2 в остальные ячейки диапазона В2:V22. Отпуская ЛКМ, получаем таблицу значений заданной функции. Фрагмент таблицы показан на рис. 2.34.

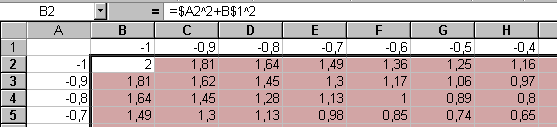
Рис. 2.34

5. Выделяем диапазон В2: V22, если он не выделен. Запускаем графический редактор Мастер диаграмм, устанавливаем тип диаграммы – Поверхность и, выполнив все необходимые шаги, получаем показанное на рис. 2.35 изображение поверхности. На рис. 2.35 дополнительно выделена Область построения диаграммы щелчком ЛКМ внутри внешней рамки после появления одноименной всплывающей подсказки.

Рис. 2.35

На поверхности, как видно из рисунка, автоматически выделяются слои уровня. Имеются дополнительные возможности форматирования, связанные с трехмерностью изображения. Щелчок ПКМ в области построения диаграммы открывает контекстное меню. Щелчком ЛКМ по строке Объемный вид вызывается диалоговое окно с пятью параметрами изображения (рис. 2.36).

Рис. 2.36

Устанавливаете новое значение параметра щелчком ЛКМ по одной из кнопок (рис. 2.37) и нажимаете кнопку Применить.

Рис. 2.37

Задания для самостоятельной работы

1. Построить кривые, заданные в полярной системе координат (при ):

а) r =  (спираль Архимеда);

б) r = (гиперболическая спираль);

в) r = (логарифмическая спираль);

г)  = 2 sin r;

д) r² + ² =100.

2. Построить поверхности (при x  [–1, 1], y  [–1, 1], h = 0,1):

а) (х + 1)² + (у+2)² +z² = 25 (сфера);

б) 3z = 2х² + у² (эллиптический параболоид);

в) z = ху (гиперболический параболоид);

г) x² +y² – z² = –1 (двуполостный гиперболоид);

^{д) (эллипсоид).}