2.5 Расчет усилий на валки при сварке сформованной полосы из стали 22гю

Усилие гиба, необходимое для осуществления внеконтактной деформации находим по формуле (2.5):

Усилие осадки кромок определяется по формуле (2.7) и равно:

По формуле (2.1) определяют полное усилие металла на валки при сварке трубной заготовки:

Вес трубной заготовки определяют по формуле (2.8):

Усилие на нижний опорный валок определяется по формуле (2.9) и равно:

Усилие на боковой валок определяют по формуле (2.10):

Усилие на верхний валок определяют по формуле (2.11):

2.6 Расчет прогиба вала

В сварочной клети вал бокового валка имеет двухопорное крепление.

Схема нагружения вала бокового валка в существующей сварочной клети изображена на рисунке 2.15.

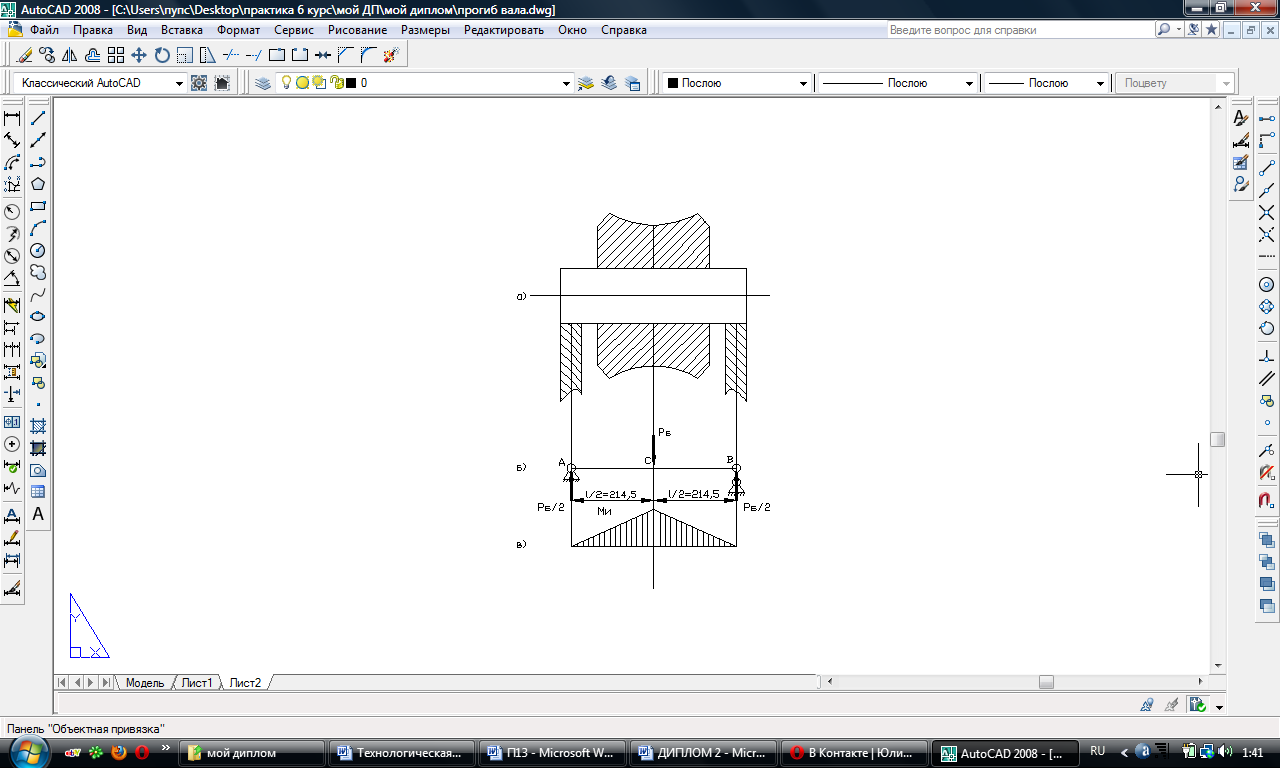
Рисунок 2.15 – Расчетная схема вала:

а) - конструкция; б) – расчетная схема; в) – эпюра изгибающих моментов.

Для определения статического прогиба в точке С вала АВ, используется метод начальных параметров. Для этого составляется уравнение прогибов, приняв начало координат в сечении А.

, (2.12)

где y₀ = 0, М₀ = 0, ₀  0, ;

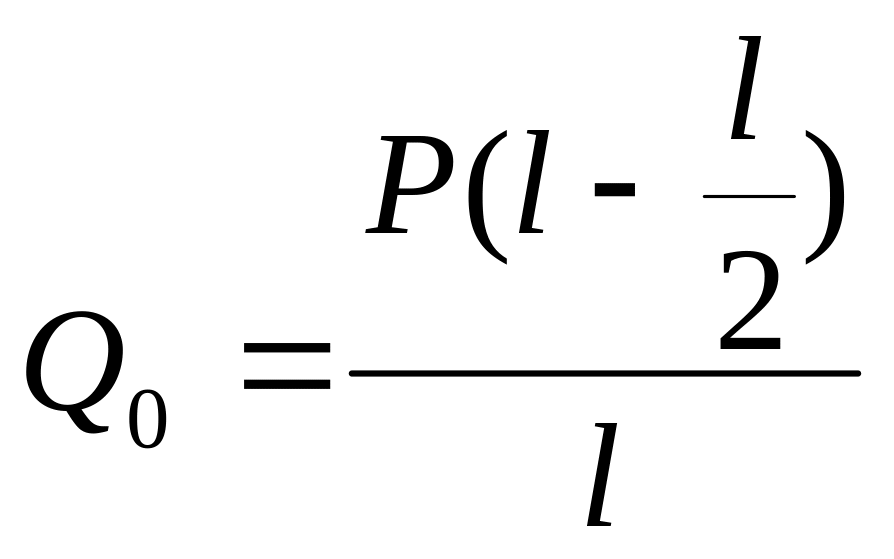M – изгибающий момент, ;

Q – поперечная сила, ;

- величина прогиба в точке Е, м;

- усилие на боковой валок, Н;

- плечо, м;

- модуль упругости, Па;

- осевой момент инерции, м⁴.

Для нахождения ₀ составим уравнение прогиба для сечения В, в котором прогиб равен нулю из условий закрепления:

Так как y₀ = 0, то, решая это уравнение, получим:

Подставив найденное значение ₀ в уравнение прогиба для се­чения С, получим формулу для определения :

, (2.13)

Осевой момент инерции для круглого сечения определяют по формуле

, (2.14)

где - диаметр вала, м.

Осевой момент инерции определяют по формуле (2.14):

Прогиб в точке С будет равен:

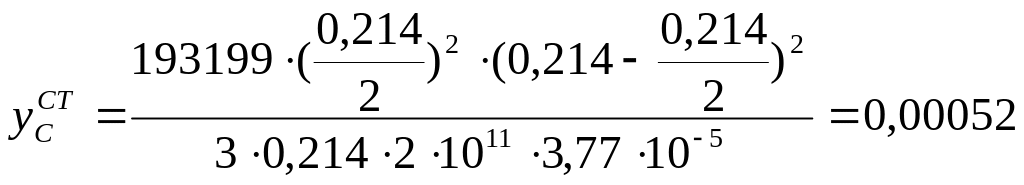м