
- •Частина і - молодша школа
- •1. Обчислити.
- •3. Заняття шахового гуртка постійно відвідували 7 учнів класу. На скільки менше учнів класу відвідували гурток, якщо тих, що його не відвідували, у 3 рази більше?
- •Частина іі - середня школа
- •Зразки розв’язування.
- •Знайдіть число якого, дорівнює 36 т.
- •З одного гектара збирають 30 т цукрового буряку, який містить цукру. Скільки цукру можна отримати з одного гектара землі засіяного цукровими буряком?
- •Розв’язання
- •6400 Грн. І 640 грн. Разом – це
- •Про ранню профілізацію
Розв’язання
За умовою задачі, після того, як вкладник взяв з банку лишку у нього на рахунку залишилось:
 лишку.
За
умовою задачі − це 3600 грн..
лишку.
За
умовою задачі − це 3600 грн..
Знаменник звичайного дробу, число 4, показує на скільки рівних частин поділене ціле, ціле – це весь лишок, а чисельник, число 3, – скільки таких частин узято, отже, 3600 грн. складаються з трьох однакових частин.
3600 : 3 = 1200 (грн.) 1/4 частина лишку;
1200 ∙ 4 = 4800 (грн.) лишок;
За умовою вкладник взяв з банку спочатку 2/7 своїх грошей і ще 640 грн., отже,
6400 Грн. І 640 грн. Разом – це
 початкового
вкладу.
початкового
вкладу.
6400 + 640 = 7040 (грн.) становлять 5/7 початкового вкладу.
Знаменник звичайного дробу, число 7, показує на скільки рівних частин поділене ціле, ціле – це весь вклад, а чисельник, число 5, – скільки таких частин узято.
7040 : 5 = 1408 (грн.) 1/7 частина всього вкладу;
1408 ∙ 7 = 9856 (грн.) весь вклад.
Відповідь: початковий вклад 9856 грн.
в) найпростіші задачі на дроби – відсотки (69 задач з повними розв’язаннями);
Зразок:
Знайдіть 25% від 20 км.
Розв’язання
Записуємо скорочену умову:
20 км − 100%;
? км − 25%.
І спосіб (через 1%)
1) 20:100 = 0,2 (км) − це 1% від 20 км;
2) 0,2∙25 = 5 (км) − це 25% від 20 км.
ІІ спосіб (за правилом)
Перетворюємо відсотки в число (для чого число відсотків ділимо на 100 і відкидаємо знак відсотків) 25% = 25:100 = 0,25.
Щоб знайти дріб від числа, можна число помножити на дріб, отже, 20∙0,25 = 5 (км).
ІІІ спосіб (за допомогою пропорції)
Позначимо невідоме число за х км.
Складаємо пропорцію:
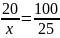 .
.
Щоб знайти невідомий середній член пропорції треба добуток крайніх членів поділити на відомий середній, отже,
 ;
;
х = 5 (км).
Відповідь: 25% від 20 км дорівнює 5 км.
ІІІ. рівняння: 110 рівнянь розбиті на блоки для відпрацювання навичок з повними розв’язаннями до них (масив містяться в «Усних тренувальних вправах з математики 5-6»);
Зразок:
− 6х = 2x −12;
Розв’язання
− 6х = 2x −12;
Доданки, що містять змінну, переносимо в ліву частину рівності, а ті що не містять − в праву, змінюючи при цьому їх знаки на протилежні.
− 6х − 2x= −12;
Зводимо подібні доданки і ділимо обидві частини отриманого рівняння на коефіцієнт біля змінної − число −8.
−8х = −12; |: (−8)
х = −12:(−8);
х = 1,5.
Відповідь: х = 1,5.
Використання таких масивів дозволяє зробити виконання дій над числами і розв’язування текстові задачі невід’ємною складовою кожного уроку, кожного домашнього завдання (перевірка правильності розв’язання і виправлення помилок при виконанні домашніх завдань є обов’язковою частиною домашнього завдання для учня) і кожної письмової роботи, що в свою чергу сприяє формуванню міцних обчислювальних навичок і навичок розв’язування задач.
Дозволяє досягти більшої ефективності довільного запам'ятовування для якого необхідним є дотримання наступних умов:
• наявність психологічної установки на запам'ятовування;
• з'ясування значення придбаних знань;
• самоконтроль, поєднання запам'ятовування з відтворенням;
• опора на раціональні прийоми запам'ятовування. [4]
Стрижневим матеріалом курсу математики, який підлягає засвоєнню в шостому класі, для подальшого успішного навчання в 7-му і подальших класах є:
дії над раціональними числами;
розв’язування задач на дроби і відсотки (через 1%, за правилом, за допомогою пропорції);
розв’язування рівнянь (з використовуванням властивостей рівнянь);
розв’язування задач за допомогою рівнянь (з обґрунтуванням);
координатна площина.
Стосовно важливості обчислювальних навичок і уміння розв’язувати текстові задачі було сказано вище. В шостому класі вводиться строге означення рівняння, кореня рівняння, поняття «розв’язати рівняння». Саме в шостому класі учень має навчитися використовувати при розв’язуванні рівняння властивості рівнянь, які в свою чергу є невід’ємною складовою розв’язування дробово-раціональних, квадратних, показникових, логарифмічних, тригонометричних та будь-яких інших рівнянь. Розв’язування рівняння в шостому класі, − це ланцюг кроків, які містять в собі такі перетворення як розкриття дужок, винесення спільного множника за дужки, зведення подібних доданків. Ці перетворення є невіддільною складовою дій над многочленами – базовим матеріалом що підлягає засвоєнню у сьомому класі і невід’ємною складовою розв’язання переважної більшості математичних задач.
Побудова точок на координатній площині за її координатами, розуміння графіків залежності між змінними величинами є складовою засвоєння такого фундаментального поняття в математиці, як функція.
Виходячи з вище сказаного завдання для учнів 7-их класів у вересні 2012-2013 навчального року було таким:
Обчислити:
 ;
;−4,04−1,29;
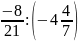 ;
;−2,9∙0,03;
 ;
;0,02:(−0,8).
2. Розв’язати рівняння: − 2(2 − 3x) = 1 − (3x + 2).
3. Побудуйте на координатній площині (одиничний відрізок 1 см) точки А(0;2), В(4;−1) і С(0;−1).
4. Від числа 97 відняли деяке число. Знайдену різницю помножили на 2 і від результату відняли 45, дістали 31. Яке число відняли від 97?
5. З пункту А в пункт В, відстань між якими 17 км, виїхав велосипедист. Через 5 хвилин на зустріч йому з пункту В виїхав другий велосипедист. Яка відстань буде між ними через 7 хвилини після початку руху другого, якщо перший їхав зі швидкістю 12000 м за годину, а другий – 21000 м за годину?
Результати виконання цієї роботи по кожному класу окремо можна бачити на діаграмі 6:
-
Дії над раціональними числами
Рівняння, що зводиться до лінійного
Побудова точок на координатній площині
Текстова задача
Ускладнена задача на рух
-
7А - 25уч.
7А - 26уч.
7А - 27уч.
7А -22уч.

-
7АН - 25уч.
7АН - 22уч.
7Б - 19уч.
7Б -26уч.

-
7Б - 16уч.
7Б - 17уч.
7В - 19уч.
7В -24уч.

Діаграма 6.
Зауважимо:
у 2009-2010 та у 2010-2011навчальних роках учням пропонувалось 10 прикладів у першому завданні;
у 2009-2010 навчальному році рівняння було таким:
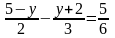 і третє
завдання було сформульовано так:
Побудуйте на координатній площині
(одиничний відрізок 1 см) точки А(0;2),
В(4;−1) і С (0;−1). Сполучіть їх послідовно
відрізками і знайдіть периметр утвореної
фігури в дециметрах. Завдання були
складнішими, ніж у наступних роках;
і третє
завдання було сформульовано так:
Побудуйте на координатній площині
(одиничний відрізок 1 см) точки А(0;2),
В(4;−1) і С (0;−1). Сполучіть їх послідовно
відрізками і знайдіть периметр утвореної
фігури в дециметрах. Завдання були
складнішими, ніж у наступних роках;у 2011-2012 н.р. у 6-Б класі математики було 7 годин, у той час як в інших 6-х класах лише 4 години на тиждень.
Наведені результати свідчать про таке:
зменшення кількості прикладів з 10-ти до 6-ти не дуже вплинуло на результати отримані учнями при виконанні обчислень;
спрощення рівняння суттєво покращило результати. Якщо у 2009-2010 навчальних роках рівняння правильно не розв’язав жодний учень із 66, то у 2010-2011 з цим завданням упоралися 7 учнів із 65 (11% − це 1 з 10), у 2011-2012 – 19 учнів із 63 (30% − це 3 з 10), а у 2013-2013 – 16 учнів із 72 (22% − це 2 з 10);
кількість годин не є визначальним показником для отримання більш високих результатів у навчанні, зауважимо що перевірявся базовий рівень навчальних досягнень у вивченні математики, що можна бачити порівнюючи результати 2012-2013 навчального року отримані 7Б класом (7 годин математики на тиждень у шостому класі) з результатами отриманими іншими сьомими класами (4 години математики на тиждень у шостому класі).
Як було зазначено вище, розв’язування рівнянь у шостому класі містить ключові елементи дій над многочленами (розкриття дужок, зведення подібних доданків тощо), отже прогнозованим є результат, який показали 8-мі класи (перевірялися навички, яких треба було набути в 7-му класі).
Виділимо декілька позицій курсу алгебри 7-го класу, які є необхідною складовою подальшого успішного навчання у 8-му класі:
додавання, віднімання і множення многочленів;
формули скороченого множення;
розкладання многочлена на множники (три основні способи: 1) винесенням спільного множника за дужки; 2) групуванням; 3) за формулами скороченого множення);
поняття функції;
розв’язування текстових задач.
Виходячи з вище сказаного завдання для учнів 8-их класів у вересні 2012-2013 навчальному році було таким:
1. Обчислити:
;
−4,04−1,29;
;
−2,9∙0,03;
 ;
;0,02:(−0,8).
2. Розв’язати рівняння: − 5(1 − 3x ) = 4 − (5x + 2).
3.
Спростити:
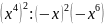 .
.
4. В одній системі координат побудувати графіки функцій:
у = −6х – 3;
у = 2.
5. Розкласти на множники многочлен:
24
 −
8
−
8 + 12
+ 12 .
.0,25
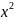 + 3
+ 3 + 9.
+ 9.− 2 + 2у –
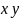 .
.
6. Скільки кілограмів 4-відсоткового і скільки грамів 10-відсоткового розчину солі треба взяти, щоб отримати 120 г 6-відсоткового розчину?
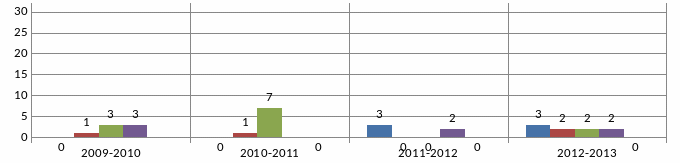
Результати виконання цієї роботи по кожному класу окремо можна бачити на діаграмі 7:
|
|
|
|
|
|
-
8А - 25уч.
8А - 23уч.
8А - 21уч.
8А -26уч.

-
8АН - 22уч.
8АН - 27уч.
8Б - 13уч.
8Б -26уч.
-
8Б - 18уч.
8Б - 23уч.
8В - 23уч.
8В -15уч.

Діаграма 7.
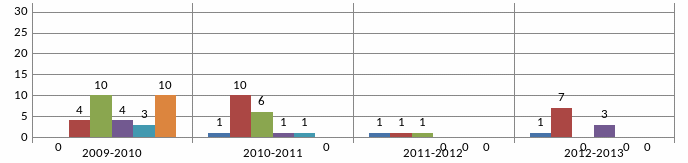
Зауважимо:
у 2009-2010 та у 2010-2011навчальних роках учням пропонувалось у першому завданні обчислити значення числового виразу на 3 дії (на кшталт:
 ),
і починаючи з 2010-2011 навчального року
– шість одно крокових прикладів;
),
і починаючи з 2010-2011 навчального року
– шість одно крокових прикладів;у 2009-2010 навчальному році учням пропонувалось у четвертому завданні розв’язати графічно систему рівнянь (на діаграмі V стовпчик);
у 2011-2012 н.р. у 7-Б класі математики було 7 годин, у той час як в інших 7-х класах лише 4 години на тиждень.
Наведені результати свідчать про таке:
зменшення кількості прикладів з 10-ти до 6-ти не вплинуло на результати перевірки обчислювальних навичок;
по закінченню 7-го класу учні не володіють навичками розкладання многочлена на множники;
кількість годин не є визначальним показником для отримання більш високих результатів у навчанні (восьмий Б поступився по всім показникам восьмому А класу, не зважаючи на те, що в 7Б було 7 годин, тоді як у 7А лише 4 години математики на тиждень).
Навички розкладання многочлена на множники є ключовими при вивченні таких тем: раціональні вирази, тема включає в себе дії над дробово-раціональними виразами і розв’язування дробово-раціональних рівнянь, усього 32 години – весь І семестр 8-го класу, перетворення ірраціональних виразів, і це тільки у восьмому класі.
У 2012-2013 навчальних роках розкласти многочлен на множники за допомогою формул скороченого множення змогли лише 6 учнів із 67, – це менше ніж один з десяти, а розв’язати текстову задачу за допомогою рівняння лише чотири із 67.
Виділимо декілька позицій курсу алгебри 8-го класу, які є необхідною складовою подальшого успішного навчання у 9-му класі:
перетворення дробово-раціональних виразів;
перетворення ірраціональних виразів;
розв’язування квадратних рівнянь (повних і не повних);
навички розв’язування дробово-раціональних рівнянь;
уміння розв’язування текстових задач за допомогою дробово-раціональних рівнянь.
Виходячи з вище сказаного завдання для учнів 9-их класів у вересні 2012-2013 навчальному році було таким:
1. Обчислити:
;
− 4,04 − 1,29;
;
− 2,9 ∙ 0,03;
;
0,02 : ( − 0,8).
2.
Спростити вираз
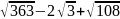 .
.
3. Знайти корені рівняння:
 ;
;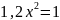 ;
; ;
; .
.
4.
Скоротити дріб:
 .
.
5. Один тракторист працював на оранці поля 7 год., після чого до нього приєднався другий тракторист. Після 5 год. спільної роботи вони закінчили оранку. За скільки хвилин міг би зорати поле кожний тракторист, працюючи окремо, якщо першому потрібно для цього на 2 год. більше, ніж другому?
Результати виконання цієї роботи по кожному класу окремо можна бачити на діаграмі 8:
-
Властивості кореня
Неповне квадратне рівняння
Повне квадратне рівняння
Скорочення дробу
Текстова задача
-
9А - 23уч.
9А - 26уч.
9А - 25уч.
9А-13уч.
-
9Б - 27уч.
9АН - 14уч.
9Б - 20уч.
9Б -21уч.
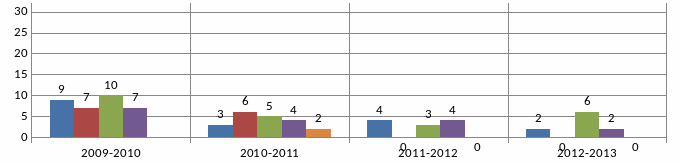
-
9В - 9уч.
9Б - 24уч.
9В - 27уч.
9В-21уч.
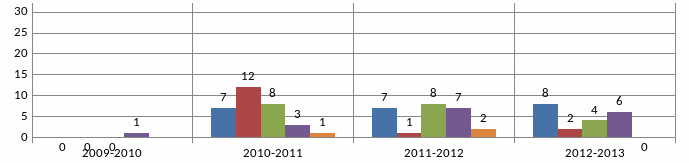
Діаграма 8.
Зауважимо:
у 2009-2010 та у 2010-2011навчальних роках учням пропонувалось у першому завданні обчислити значення числового виразу на 3 дії (на кшталт: ), і починаючи з 2010-2011 навчального року – шість одно крокових прикладів;
у 2009-2010 навчальному році робота не містила текстової задачі.
У наведеній діаграмі звернемо увагу на результати розв’язання квадратного рівняння:
2009-2010 н.р.
неповне квадратне рівняння правильно розв’язали 8 учнів з 59 (14%);
повне квадратне рівняння правильно розв’язали 13 учнів з 59 (22%);
2010-2011 н.р.
неповне квадратне рівняння правильно розв’язали 19 учнів з 64 (28%);
повне квадратне рівняння правильно розв’язали 20 учнів з 64 (31%);
2011-2012 н.р.
неповне квадратне рівняння правильно розв’язали 1 учень з 72 (1%);
повне квадратне рівняння правильно розв’язали 11 учнів з 72 (15%);
2012-2013 н.р.
неповне квадратне рівняння правильно розв’язали 4 учнів з 55 (7%);
повне квадратне рівняння правильно розв’язали 12 учнів з 55 (23%).
Для розуміння проблеми пов’язаної з відсутністю навичок розв’язування квадратних рівнянь виділимо розділи алгебри, тільки за 9-й клас, засвоєння яких безпосередньо залежать від цієї навички:
Квадратична функція;
Побудова графіка функції у=ах2+вх+с;
Алгебраїчне дослідження властивостей квадратної функції;
Розв’язування квадратних нерівностей за допомогою графіка квадратної функції;
Розв’язування раціональних нерівностей методом інтервалів;
Перетворення ірраціональних виразів;
Розв’язування ірраціональних рівнянь;
Рівняння з двома змінними та його графік;
Системи двох рівнянь з двома змінними;
Текстові задачі, які зводяться до розв’язування систем.
На діаграмі 9. можна бачити результати написання цієї роботи учнями Українського колежу за 2011-2012 та 2012-2013 навчальні роки та результати написання даної роботи у 2012-2013 навчальному році в одній із загальноосвітніх шкіл м. Києва.

Діаграма 9.
У СШ№…(О.И.) роботу виконували 26 учнів. З них правильно розв’язали неповне квадратне рівняння – 0 учнів, повне – 0 учнів. З 26 учнів тільки одна дитина правильно розв’язала тільки одне завдання – скоротила дріб.
Розв’язування текстових задач у восьмому (після вивчення теми: Квадратні рівняння)- дев’ятому класах зводиться до розв’язання квадратного або дробово-раціонального рівняння. Про яку текстову задачу може йти мова?
Хочеться відмітити, більш високі результати в Українському колежі ім. В. О. Сухомлинського у порівнянні із СШ№…(О.И.), можна спостерігати тільки тому, що в колежі більша частина батьків приймає участь у навчанні своєї дитини (не за рахунок передових методик навчання). Іншими словами – працюючи за існуючою технологією вчитель неспроможний отримати позитивний результат як в молодшій, так і в середній, так і в старшій загальноосвітній школі.
Про що говорять наведені результати? – навчання математики в загальноосвітніх школах України перетворилося на фарс. Підстав вважати,що в інших загальноосвітніх школах ситуація краща, – на жаль немає. Подивіться на результати ЗНО з математики. Вчителі роблять вигляд що навчають, а учні, – що навчаються. Причому частина вчителів старанно виконують свою роботу. Це говорить про те, що діючі сьогодні програми, методики і технології навчання не діють.
Сьогоднішні дев’ятикласники є випускниками тих вчителів молодшої школи, діти яких навчаються зараз у п’ятому класі (2012-2013 н.р.). А це за результатами зрізів одна з найсильніших паралелей (можна порівняти хіба що з п’ятикласниками 2012-2013 н.р.).
Сподіватись на те, що під час навчання у 5-8 класах відбудуться зміни на краще не дають підстав дані наведені в діаграмі 10.
Незалежно від кваліфікації вчителя, який працює в класі, іде пониження рівня навченості математики. Так на діаграмі 10 − це можна бачити на кількості учнів, які правильно розв’язали текстову задачу.

Діаграма 10.
