1.4.2.Расчет и построение выходного напряжения

Реакцию цепи находим на каждую гармонику входного напря­жения в отдельности- Результирующая реакция равна сумме со­ставляющих реакпий.

Амплитуда n-й гармоники на выходе согласно передаточной функции определяется выражением:

U_2mⁿ = H_U(n∙ω₁)∙U_1mⁿ

где

Фаза n-й гармоники иа выходе определяется выра­жением

φ(n∙ω₁) = argH(j∙n∙ω₁) =

φ*(n∙ω₁) = 0.

Реакция выходного напряжения на постоянную состав­ляющую входного напряжения:

частота ω₀=0; амплитуда H_U(nω₁)∙U₁⁰ = 0,00∙0,50 = 0,00 B;

начальная фаза φ₂⁰ = 90°.

Реакции на последующие гармоники:

1 гармоника: частота ω₁ = 1∙6,28∙10³ 1/c; амплитуда U₂¹ = 0,75∙0,64 = 0,48 B;

начальная фаза φ₂¹ = 46°.

2 гармоника: частота ω₂ = 3∙6,28∙10³ 1/c; амплитуда U₂² = 0,55∙0,21 = 0,12 B;

начальная фаза φ₂² = 53°.

3 гармоника: частота ω₂ = 5∙6,28∙10³ 1/c; амплитуда U₂³ = 0,33∙0,13 = 0,04 B;

начальная фаза φ₂³ = 63°.

4 гармоника: частота ω₂ = 7∙6,28∙10³ 1/c; амплитуда U₂⁴ = 0,23∙0,09 = 0,02 B;

начальная фаза φ₂³ = 69°.

Амплитудный и фазовый спектры первых гармоник напряже­ния U₂(t) показаны на рис. 1.8, 1.9.

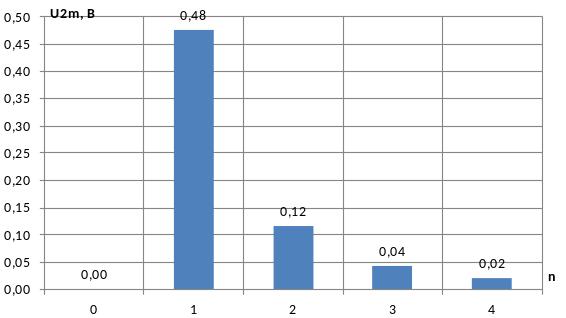
Рис. 1.8. Амплитудный спектр первых гармоник напряже­ния U₂(t)

Рис. 1.9. Фазовый спектр первых гармоник напряже­ния U₂(t)

Составляющие выходного напряжения:

U₂⁰ = 0,00 В. φ=90°

U₂¹(t) = 0,48∙cos(1∙6,28∙10³t+46°)

U₂²(t) = 0,12∙cos(3∙6,28∙10³t+53°)

U₂³(t) = 0,04∙cos(5∙6,28∙10³t+63°)

U₂⁴(t) = 0,02∙cos(7∙6,28∙10³t+69°)

Результирующее выходное напряжение

U₂(t) = U₂⁰ + U₂¹(t) – U₂²(t) + U₂³(t) – U₂⁴(t)

Первые гармоники разложения и их результирующая приведе­ны на рис. 1.7.

Рис. 1.10. Первые гармоники выходного напряжения,

2.Расчет переходных процессов в цепи

2.1.Определение переходной и импульсной функций

Получим переходные процессы в цепи как реакцию на единич­ный скачок h_U(t), импульс вида δ-функции g_U(t), скачок заданной величины U₁(t), импульс напряжения сложной формы U₁(t).

Переходная h_U(t) и импульсная g_U(t) функции определяют вид, скорость затухания и продолжительность переходного процесса. Функции используются при определении реакции цепи на входной сигнал произвольной формы по интегралу или сумме Дюамеля.

Переходная функция h_U(t) определяет собой переходный про­цесс, возникающий при подаче на вход цепи скачка напряжения 1 В, такое воздействие определяется единичной ступенчатой функ­цией (рис. 14).

Рис. 2.1. Единичная ступенчатая функция

Ступенчатая функция отражает распространенный вид входно­го воздействия при подаче на вход цепи ступенчатого напряжения, коммутации цепи, а в электромеханических устройствах при рез­ком изменении нагрузки электрического генератора или нагрузки на валу двигателя.

Импульсная функция g_U(t) определяет собой реакцию цепи на входное воздействие в виде δ-функции (рис. 2.2).

Рис. 2.2. Единичная δ-функция

По определению δ-функция равна производной от единичной ступенчатой функции 1(t), поэтому импульсная функция равна производной от переходной функции

g_U(t) = h'_U(t).

Дельта-функция тождественно равна нулю повсюду, кроме точ­ки t = 0, где она стремится к бесконечности. Основное свойство δ-функции заключается в том, что

функция имеет единичную площадь и размерность (сек^-1).

Поскольку функция Н_U(р) цепи ранее определена, то воспользу­емся преобразованием Лапласа. Переходная функция

По таблице преобразований Лапласа находим оригинал пере­ходной функции (приложение 4)

=

,

где α = - р₁^П = ; β = - р₂^П

р^П₁ = -10000; р^П₂ = -7500

Подставляем численные значения. Получаем

h_U(t) = 4,00∙e^-10000t – 4,00∙e^-7500t

Зависимость h_U(t) приведена на рис. 2.3.

Рис. 2.3. Пере­ходная функция h_U(t)

Находим импульсную функцию g_U(t)

Воспользу­емся преобразованием Лапласа.

По таблице преобразований Лапласа находим оригинал импульсной функции (приложение 4)

=

,

где α = р₁^П ; β = р₂^П

р^П₁ = -10000; р^П₂ = -7500

Подставляем численные значения. Получаем

h_U(t) = 40000∙e^-10000t – 30000∙e^-7500t

Зависимость g_U(t) приведена на рис. 2.4.

Рис. 2.4. Импульсная функция g_U(t)