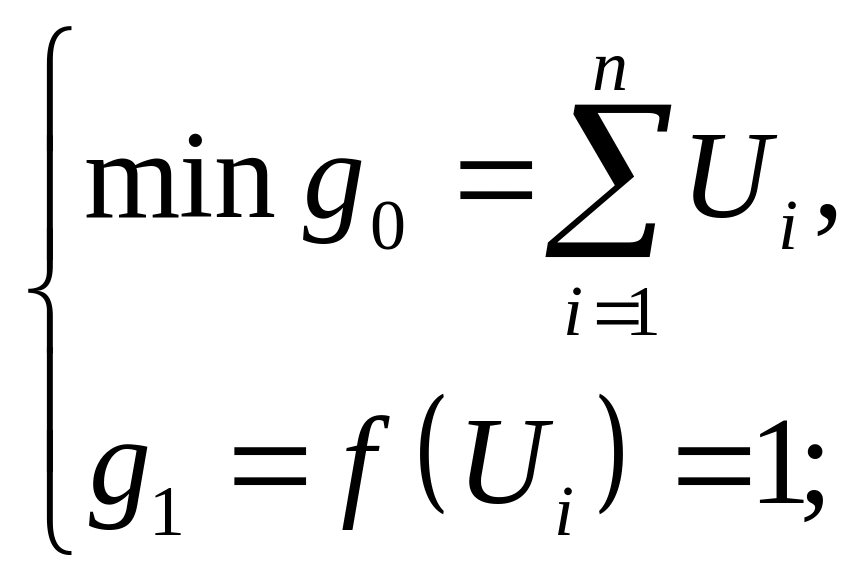- •1.1 Основные проблемы конструирования эвм.
- •1.2 Методы повышения надежности.
- •2.1 Выбор формы и определение размеров типовых конструкций.
- •2.2 Модульный принцип конструирования.
- •3.1 Выбор оптимальных соотношений размеров панели.
- •3.2. Теплообмен естественной конвекцией.
- •2. Теплообмен плоской и цилиндрической стенок
- •4.1 Основные тенденции развития вт, влияющие на конструирование
- •4.2 Расчет геометрических размеров панели и тэз.
- •(Конкретный пример смотри в книге на страницах 25-26)
- •5.1 Выбор оптимальных соотношений размеров многорамной стойки.
- •5.2 Тепловые модели конструкций эвм. Методика их получения.
- •6.1 Расчет геометрических размеров многорамной стойки при заданной задержке сигнала.
- •6.2 Способы уменьшения помехи по цепям управления.
- •7.1 Расчетная модель конструкции эвм как механической системы, характеристика ее качества. Определение реакции конструкции на виброускорение.
- •7.2 Выбор формы типовых конструкций. Основные схемы геометрической компоновки.
- •8.1. Перекрестная помеха. Рекомендации по конструированию линий связи.
- •4. Возможность отдельного анализа ёмкостной и индуктивной составляющей пп.
- •8.2. Характеристики надежности км при вибрациях, рекомендации по использованию видов вибрации для испытания элементов и км .
- •9.1. Цель и принципы конструкторского проектирования.
- •9.2. Определение теплового сопротивления от корпуса ис к каркасу блока.
- •10.1. Теплообмен в конструкции эвм.
- •10.2. Графический метод оценки искажений сигналов от эффекта отражений в линиях связи схем ттл.
- •11.1. Помехи по цепям управления. Рекомендации по конструированию цепей управления.
- •11.2. Теплообмен вынужденной конвекцией.
- •1.Продольное обтекание
- •2.Поперечное обтекание
- •12.1. Индуктивная составляющая перекрестной помехи. Способы ее уменьшения.
- •12.2. Методика получения тепловых моделей конструкций эвм.
- •13.1. Определение теплового сопротивления типовых конструкций при теплообмене кондукцией.
- •13.2. Анализ взаимодействующих цепей связи элементов эвм.
- •14.1. Типовые конструкции. Их основные элементы.
- •14.2. Помеха по шинам питания. Способы ее уменьшения.
- •15.1 Выбор вида печатной платы в зависимости от быстродействия схем
- •15.2 Методика получения модели конструкции эвм как механической системы. Анализ элементов конструкции
- •16.1 Определение допустимой длины взаимодействующих линий связи
- •16.2 Основные элементы типовых конструкций
- •17.1 Одноуровневые и многоуровневые принципы конструирования
- •17.2 Анализ искажений сигналов в несогласованных линиях связи
- •18.1 Основные задачи конструкторского проектирования
- •18.2 Определение допустимой длины несогласованной линии связи
- •19. 1. Показатели надежности невосстанавливаемых эвм.
- •19.2. Способы уменьшения перекрестной помехи.
- •20. 1. Классификация нестационарных эвм. Виды механических воздействий на них. Основные задачи конструирования.
- •20.2. Определение тепловых сопротивлений пакета субблоков.
- •Элементарная ячейка пакета субблоков.
- •21. 1. Геометрическая компоновка конструкции эвм.
- •21.2. Теплообмен естественной конвекцией.
- •2. Теплообмен плоской и цилиндрической стенок
- •22.1 Оценка надежности эвм как сложного объекта.
- •22.2 Тепловой режим конструкции эвм. Способы переноса тепловой энергии.
- •23.1 Емкостная составляющая перекрестной помехи. Способы ее уменьшения
- •P.S. Прошу прощения, со способами уменьшения не разобрался
- •23.2 Теплообмен кондукцией
- •24.1 Показатели надежности восстанавливаемых эвм
- •24.2 Расчет теплового сопротивления корпуса ис-каркаса блока.
- •Возможно к этому же вопросу относятся слайды 4.39 и 4.40
- •25.1 Виды отказов из-за механических взаимодействий. Определение вида вибрационного воздействия и его свойств, влияющих на работоспособность эвм.
- •25.2 Определение понятия «надежность». Основные свойства надежности.
- •26.1 Соотношения между емкостной и индуктивной составляющих перекрестной помехи
- •26.2 Оценка показателей надежности конструктивных модулей.
- •27.1. Способы замены широкополосной случайной вибрации.
- •27.2. Виды, объекты применения бис и основные задачи конструктора.
- •28.1. Математическая модель конструкции эвм с сосредоточенными параметрами.
- •28.2. Основные проблемы конструирования и применения бис.
- •29.1. Оценка качества конструкции как механической системы.
- •29.2. Виды корпусов бис.
- •30.1. Расчетная модель конструкции с сосредоточенными и распределенными параметрами.
- •31.1. Частоты и формы собственных колебаний печатной платы как тонкой пластины. Сопоставление способов ее крепления граничным условиям.
- •31.2. Особенности конструирования эвм на микропроцессорах.
- •32.1. Исследование печатной платы по неполной системе собственных функций.
- •32.2. Методы и элементы электрических соединений бис.
- •33.1. Анализ способов крепления плат. Пример способа, порождающего условие зажатого края. Рекомендации по улучшению качества несущих конструкций.
- •33.2. Внутри и межплатные соединения аппаратуры на бис.
4.2 Расчет геометрических размеров панели и тэз.
Решим задачу определения оптимальной геометрии функциональных устройств, размещаемых в панелях или блоках, для обеспечения минимальной потери быстродействия в линиях связи внутри них. Общей компоновочной схемой субблоков в блоках стационарных ЭВМ является двухмерная, показанная на рис. 3.
Сформулируем задачу определения оптимальной геометрии блока как задачу геометрического программирования. Длина части линии связи, проходящая внутри типового элемента замены, зависит от качества решения задачи трассировки соединений между микросхемами. В некоторых случаях при размерах типового элемента замены 140 X 150 мм длина линии связи в блоке достигает значения 600 мм. Запишем ее в виде , тогда
(10)
где - коэффициент, учитывающий качество трассировки (при отсутствии ограничений на длину связей в ТЭЗ ). Объем блока
(11)
На основании (10) и (11) целевая функция задачи будет: при ограничении .
Решение задачи дает следующие результаты: минимальная длина линии связи блока
(12)
оптимальное соотношение геометрических размеров блока
(13)
Выражения для расчета размеров при заданном значении длины линии связи будут:
(14)
(15)
(Конкретный пример смотри в книге на страницах 25-26)
5.1 Выбор оптимальных соотношений размеров многорамной стойки.
Одна из проблем, которые решаются при разработке конструкции ЭВМ, – сокращение потерь быстродействия из-за конечной скорости распространения сигналов по линиям межэлементных связей.
Общая задержка сигналов при преобразовании информации складывается из задержек сигналов tз.л.э в логических элементах и времени распространения сигналов tз.л.с в линиях связи.
Длина линии связи между наиболее удаленными участками типовой конструкции зависит от ее компоновочной схемы. В связи с этим возникает задача выбора такой пространственной геометрии конструктивного модуля, которая при данном его объеме обеспечивала бы минимальную длину линии связи.
Последовательность решения задачи:1)выбрать критерий оптимизации;2)разработать модель;3)выявить влияющие факторы, т.е. варьируемые параметры;4)определить ограничения;5)найти зависимость целевой функции от варьируемых параметров;6)получить формальную постановку задачи;7)выбрать метод решения и реализовать его, выполняя необходимые преобразования.
Критерий – минимум длины линии связи между двумя наиболее удаленными точками конструктивного модуля.
Возможные методы решения:1)Поиск экстремумов функции.2)Использование методов теории геометрического программирования – совокупность методов решения комбинаторных задач непрерывной оптимизации.
Стандартная формулировка задачи геометрического программирования:
Найти
![]() ,
при
,
при
![]() ,
где
,
где
![]() – варьируемые параметры,
– варьируемые параметры,
![]()
Ограничения:
![]()
Ui – полином с положительными коэффициентами (позином);
ai,j – произвольные вещественные числа.
На основании теории двойственности минимум суммы g0 сводится к максимуму двойственной функции v0.
Например при
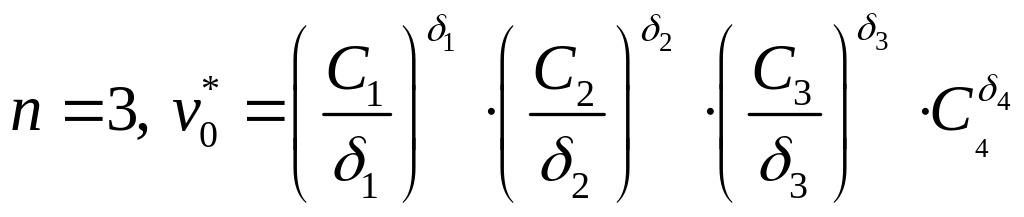 (1), где
(1), где
![]() – оптимальное решение.
– оптимальное решение.
Далее составляется система:
Для ортогональности: |
Для нормализации: |
|
|
![]() ;
; ![]()
Отсюда следует,
что![]()
Подставим эти
значения в (1) и получим:
![]()
При этом
![]()
Оптимальное соотношение Lb, Lh, Ll позволяет найти следующее положение теории геометрического программирования: в точке оптимума целевой функции (ЦФ) коэффициенты di показывают вклад составляющих ЦФ в её оптимальное значение:
![]() (2)
(2)
тогда ;при ; ; ,
имеем:
![]()
При известном
значении
значение
![]() на основании (2) вычисляются как:
на основании (2) вычисляются как:
![]() ,
,
![]() ,
,
![]()