2.1.2 Построение расчетных сеток

В данной работе рассматриваются двумерные разностные сетки. Под такой сеткой подразумевается некоторая совокупность координат узловых точек, упорядоченных по каждому из двух целочисленных индексов. Соединив линиями узлы сетки, соседние по каждому из индексов (такая операция называется восполнением линий сетки), тогда образуются два семейства линий, которые разрезают участок плоскости на примыкающие друг к другу четырехугольники, называемые ячейками сетки. Если они примыкают без наложений и зазоров, будем говорить о регулярной разностной сетке для области Ω, границы которой естественно определяются множеством узлов сетки и способом восполнения ее линий.

Процесс построения расчетной сетки относится к ключевым моментам проведения численного эксперимента. Согласно статье [4] рациональным выбором сетки можно значительно упростить и улучшить численное решение задач МСС, как правило, представляющих системы нелинейных дифференциальных уравнений в частных производных, а затем, при численном дифференцировании, системы алгебраических уравнений большого размера.

Задача построения расчетной сетки заключается в нахождении отображения, которое переводит узлы сетки из физической области в вычислительную. Данное отображение, как минимум, должно удовлетворять следующим требованиям:

• отображение должно быть однозначным;

• сетка должна иметь сгущение в тех областях, где возможно появление больших градиентов искомых функций;

• линии сетки должны быть гладкими для обеспечения непрерывности производных.

Сетка выступает объектом для расчета, т.е. именно на нее накладывается математическая модель поведения вещества.

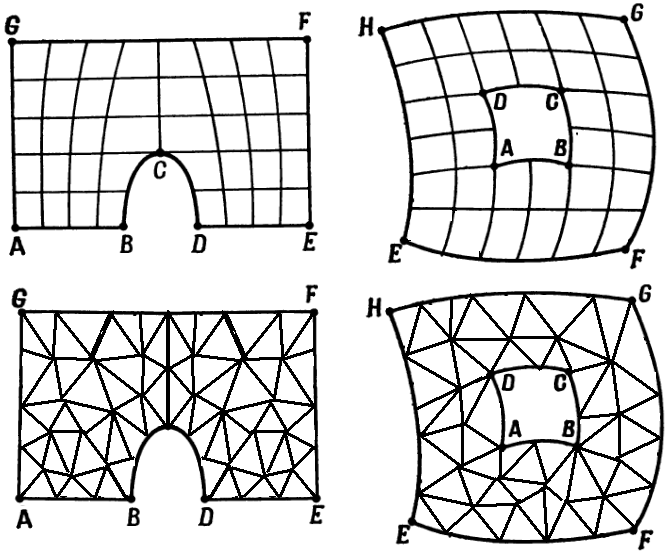
Различают два основных вида расчетных сеток, представленных на рисунке 2.3:

• регулярные (structured grids);

• нерегулярные (unstructured grids).

а

б

Рисунок 2.3 – Расчетные сетки: а – регулярная сетка; б – нерегулярная сетка;

Регулярная (структурированная) сетка – это упорядоченная структура с явно выраженными сеточными направлениями, которые, в общем случае, представляют собой криволинейную систему координат. В преобразованном (вычислительном) пространстве ячейки сетки являются топологическими прямоугольниками (двумерные задачи) или параллелепипедами (трехмерные задачи).

Характерной особенностью нерегулярных (неструктурированных) сеток является «произвольное» расположение узлов сетки в физической области. Произвольность следует понимать в том смысле, что отсутствуют сеточные направления и структура, подобная регулярным сеткам. Узлы сетки объединяются в многогранники (трехмерный случай) или в многоугольники (плоский случай) произвольной формы.

Данная работа направлена на управление методами и параметрами оптимизации двумерных сеток.

2.3 Общая характеристика оптимизации расчетных сеток с использованием оптимизатора Mesquite

Качество расчетной сетки относится к ее геометрическим свойствам. При отсутствии контроля над формой, гладкостью и ориентацией сетки, возникает отрицательное влияние на точность решения и вычислительную эффективность численного моделирования.

Качество сетки необходимо отслеживать на всех этапах процесса генерации. Это обусловлено тем, что существует ряд геометрических свойств (гладкость, углы, пропорции и ориентация) сетки, которые могут влиять на точность решения задачи численного моделирования. Моделирование с использованием расчетных сеток требует изначально такие геометрические свойства, которые будут удовлетворять решению и не ухудшать точность. В дополнение к точности решения геометрические свойства оказывают влияние на количество машинного времени, необходимого для получения численного решения.

Оптимизация расчетных сеток является важным в текущей области исследований. На сегодняшний день остаются открытые вопросы, одним из которых является трудность оптимизации расчетной сетки в одном программном пакете, но созданной в другом программном пакете.

Именно эти и другие аспекты легли в основу создания библиотеки Mesquite.