1 Постановка задачи
Процесс оптимизации расчетной сетки состоит из решения нескольких последовательных задач, к каждой из которых при необходимости можно вернуться для изменения методов и параметров:
– графическое обеспечение всего процесса оптимизации;
– оптимизация расчетных сеток;
– сохранение результатов оптимизации;
– интерфейс пользователя для интерактивной работы с моделями и с параметрами;
– вычисление мер оценки качества оптимизированной сетки;
– сохранение координат узлов сеток и характеристик ячеек и узлов в файл для передачи в программы численного моделирования.
В системе GeomGrid2 планируется реализовать решение всех перечисленных задач.
На рисунке представлена поэтапная схема функционирования сервисной системы GeomGrid2.
Целью настоящего дипломного проекта является внедрение управления методами и параметрами для оптимизации расчетных сеток МСС в реакторных установках.
Под оптимизацией понимается улучшение качества расчетной сетки.
(рисунок)
В задании на дипломный проект были поставлены следующие задачи:
– реализовать тестовый проект на языках C++ и C# в среде разработки Visual Studio 2008, платформа .NET2.0 для использования функций оптимизатора Mesquite;
– обеспечить графическое обеспечение процесса оптимизации расчетных сеток;
– разработать программу импорта и экспорта функций оптимизатора Mesquite;
– стыковать программу GeomGrid2 с библиотекой Mesquite;
– внедрить оптимизатор Mesquite в программу GeomGrid2;
– разработать интерфейс пользователя для интерактивной работы с методами и функциями библиотеки Mesquite.
2 Анализ современных подходов к оптимизации 2d расчетных сеток
2.1 Анализ процесса математического моделирования механики сплошной среды (мсс)
Трудно представить современную науку, технику, промышленность без широкого применения математического моделирования. Сущность методологии математического моделирования состоит в замене исходного физического объекта его математической моделью и в последующем изучении этой модели с помощью вычислительных методов.
В работе [1] утверждается, что применение математического моделирования и вычислительного эксперимента имеет ряд преимуществ над традиционными методами познания (теоретический анализ и натурный эксперимент) и позволяет:
выявить ошибки проектирования изделия;
оценить качество проекта до стадии производства;
исследовать процессы, масштабируя их длительность во времени и варьируя параметры;
снизить затраты ресурсов (временных, финансовых и др.) за счет замены натурного эксперимента моделированием.
Постановка вопроса о математическом моделировании какого-либо объекта, согласно [1], порождает план действий из трех этапов: модель – алгоритм – программа, как показано на рисунке 2.1.
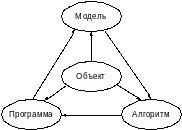
Рисунок 2.1– Составляющие математического моделирования
На первом этапе строится «эквивалент» объекта, отражающий в математической форме важнейшие его свойства: законы, которым он подчиняется, связи, присущие его частям и т.д.
Второй этап – выбор или разработка алгоритма для реализации модели на компьютере. Модель представляется в форме, удобной для применения численных методов.
На третьем этапе создаются программы, «переводящие» модель и алгоритм на доступный компьютеру язык. Их можно назвать «электронным эквивалентом» изучаемого изделия, пригодным для вычислительного эксперимента.
Как указано в [1], под вычислительным экспериментом следует понимать определение свойств и характеристик рассматриваемого явления, процесса, объекта путем решения с помощью ЭВМ системы уравнений, представляющих математическую модель объекта.