113. Прочность бетона на сжатие и растяжение (кубиковая и призменная).

Кубиковая прочность – временное сопр. обр. куба при сжатии (R). При осевом сжатии кубы разрушаются вследствие разрыва Б в поперечном направлении. R=Nвр/A, Nвр – разрушающая сила, A – площадь поперечного сеч. образца

Кубиковая прочность не отражает фактическую прочность Б в констр.

Призменная прочность – временное сопр. обр. призмы сжатию (Rb).

Rb=Nвр/A

Rb≈0,75R

Растяжение (Rbt). Прямой и косвенный метод.

Прямой – испытание образца восьмерки (метод технически сложен).

Косвенный (1 из них) – испытание на изгиб Б балок с созданием зоны чистого изгиба

Rbt=(0,5Nвр*a)/Wpl, где Wpl – упруго-пласт. момент сопр., Wpl=bh²/3,5

1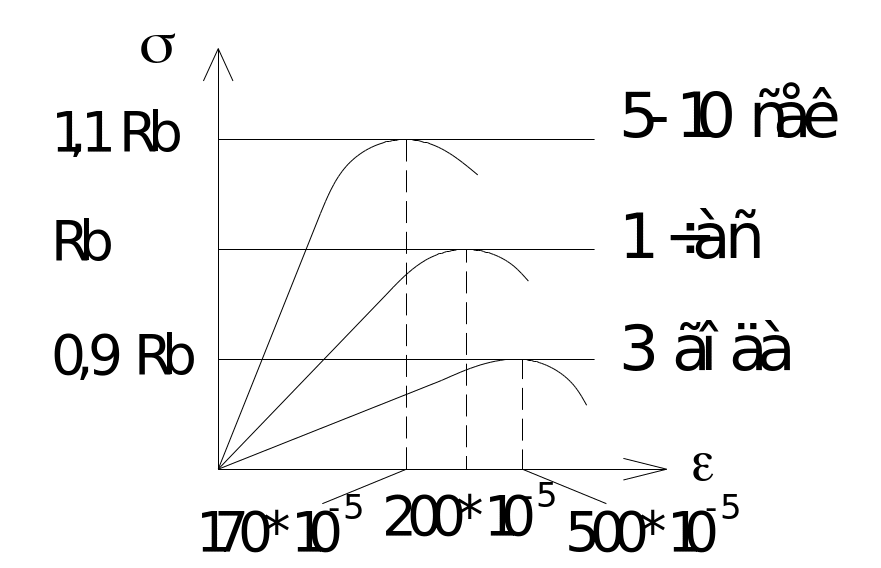 14. Прочность бетона при кратковременном, длительном и многократном загружении.

График

При мгновенном действии расч. усилий в констр. (ветровая, подвижная и т. д. нагр.) коэф. усл. работы, учитывающий продолжительность действия нагр.: γb2=1,1;

при кратковременном действии: γb2=1;

по кратковр. исп. обр. Б получают вр. сопр. сжатию;

при длительном действии нагр. (плиты и балки перекрытий, колонны многоэт. зд.): γb2=0,9;

при растяжении (для всех видов Б, кроме ячеистого): γbc=1,3.

115. Деформативность бетона, модули упругости, понятие о ползучести.

Деформативность. Б – упруго-пласт. мат-л. Зависимость «σ-ε» - нелинейна. Разл. объемные (не зависят от нагр.) и силовые деф-и. Объемные: темп. и влажностные (усадка и набухание). Силовые. Зависят от нагр. и состоят из упругой и пластической части.

Деф-е хар-ки Б: нач. модуль упругости Б – Eb; коэф. упругопластичности – ν.

Зависимость «σ-ε» для Б (рисунок).

Ползучесть – св-во Б деф-ся при неизменных напр. (нарастание деф. при выдержке обр. под нагр.).

Зависимость «σ-ε», (рисунок)

α – угол наклона линейной зависимости в нач. координат.

При σ_i=0,3Rb – упр. работа Б, ε_пл=0, Eb=tgα=σi/εyi. Нач. модуль упр. = const, исп. его можно получить только нач. деф.: εyi= σi/Eb.

Полные деф-и: Eb’=tgβ=σi/εi, Eb’ – секущий модуль

При проектировании: Eb’= Eb’*ν, ν – коэф. упругопластичности.

Продольные деф-и можно опр-ть с помощью коэф. Пуассона: μ=ε_попер/ε_прод=0,2

116. Классификация арматуры, арматурные изделия.

См. Вопрос 103

117. Три стадии напряженно-деформированного состояния сечений.

Рассматривается норм. сеч. в зоне чистого изгиба балки. При ув. нагр. сеч. проходит 3 стадии НДС.

1 ст. НДС – работа без трещин в растянутой зоне. Стадия хар-на: в начале упругой работой сжатого и раст. Б; в конце стадии с ув. нагр. – упругая работа сжатого Б и упругопласт. растянутого с напр. в крайнем раст. волокне = прочность на осевое напр.: σbt=Rbt

Расч. схема сеч. (рисунок)

1 ст. НДС исп. для расчета эл-в по обр. трещин (2 гр. пред. сост.). Опр. момент трещинообр. Mcrc=Rbtser*Wpl, Mcrc≥M1

2 ст. НДС – устойчивая работа с трещинами в раст. зоне. Упругопласт. Работа сжатого и оставшегося раст. Б с ординатой Rbt вверху трещины, активное подключение раст. ар-ры.

Расч. схема сеч. (рисунок)

2 ст. НДС исп. для расчета прогибов и ширины раскрытия трещин (2 гр. пред. сост.)

3 ст. НДС – разрушение норм. сеч. Хар-р разрушения в осн. зависит от кол-ва ар-ры.

Разрушение по текучести ар-ры. Раскрытие трещин, прогибы. Б недогружен. Разрушение плавное контролируемое.

Разрушение от раздробления сжатого Б при повышенном содерж. ар-ры. Б перегружен, ар-ра недогружена. Разрушение хрупкое внезапное неконтролируемое.

Расч. схема сеч. (рисунок)

118. Прямоугольные сечения изгибаемых элементов с одиночной арматурой, проверка прочности.

Расчетная схема сечения (рисунок)

Задача – проверка прочности.

Дано: b, h, Rb, Rs, As, a, M. Проверить: M≤Mu

Решение:

ξR. 2. h0=h-a. 3. x – опр. высоты сжатой зоны, (Rs*As)/(Rb*b). 4. Опр. относительной высоты сжатой зоны ξ=x/h0≤ξR, если ξ>ξR, принимаем ум. знач. x=xR, xR=ξR*h0. 5. Опр. несущей способности сеч.: Mu=Rb*b*x*(h0-0,5x), Mu=Rs*As*(h0-0,5x). 6. Проверка 1 гр. пред. сост., если M≤Mu, то прочность обеспечена.

119. Прямоугольные сечения изгибаемых элементов с двойной арматурой, проверка прочности.

Расчетная схема сечения (рисунок)

Задача – проверка прочности.

Дано: b, h, Rb, Rs, Rsc, As, As’, a, a’, M. Проверить: M≤Mu

Решение:

1. ξR. 2. h0=h-a. 3. x – опр. высоты сжатой зоны, (Rs*As-Rsc*As’)/(Rb*b). 4. Опр. относительной высоты сжатой зоны ξ=x/h0≤ξR, если ξ>ξR, принимаем ум. знач. x=xR, xR=ξR*h0. 5. Опр. несущей способности сеч.: Mu=Rb*b*x*(h0-0,5x)+Rsc*As’*(h0-a’). 6. Проверка 1 гр. пред. сост., если M≤Mu, то прочность обеспечена.

120. Понятие об эквивалентной ширине сжатой полки.

Эквивалент – рав-во по какому-л. параметру. Из-за того, что полка таврового сеч. при изгибе вовлекается в работу с ребром неравномерно, расч. сеч. может иметь расч. ширину полки (bf’) < фактической на основании эквивалентности эпюр сжатия в полке по площади.

bf’ – эквивалентная по площади эпюры сжатия ширина полки. Чем тоньше полка, тем < bf’ по сравнению с b_полки.

121. Тавровое сечение изгибаемых элементов, проверка прочности при границе сжатой зоны в полке.

Расчетная схема сечения (рисунок)

Задача – проверка прочности.

Дано: b, h, b_f’, h_f’, Rb, Rs, As, a, M. Проверить: M≤Mu, ξ≤ξ_R

Решение:

1. ξ_R. 2. h0=h-a. 3. Опр. случая расчета: если Rs*As≤Rb*b_f’*h_f’ – граница сжатой зоны в полке. Рассматривается прямоуг. сеч. шириной b_f’. 4. Опр. высоты сжатой зоны: x=(Rs*As)/(Rb*b_f’). 5. ξ=x/h0≤ξ_R, если ξ>ξ_R, то для надежности принимается ум. знач. = граничному: x=x_R= ξ_R*h0. 6. Опр. несущей способности сеч.: Mu=Rb*b_f’*x*(h0-0,5x).

Если Rs*As>Rb*b_f’*h_f’ – граница сжатой зоны в ребре. 4. x=(Rs*As-Rb*( b_f’-b)*h_f’)/(Rb*b). 5. ξ=x/h0≤ξ_R, если ξ>ξ_R, то для надежности принимается ум. знач. = граничному: x=x_R= ξ_R*h0. 6. Опр. несущей способности сеч.: Mu=Rb*b*x*(h0-0,5x)-Rb*( b_f’-b)*h_f’*(ho-0,5h_f’). Если M≤Mu, то прочность обеспечена.

122. Тавровое сечение изгибаемых элементов, проверка прочности при границе сжатой зоны в ребре.

см 121

123. Наклонные сечения на действие поперечной силы, схема разрушения, расчетная схема сечения.

Разрушение от перерезывающей силы происходит от касательных напр. сдвига среза.

Схема разрушения (рисунок)

Разрушение внезапное неконтролируемое. Обязателен расчет по 1 гр. пред. сост.

Расч. схема наклонного сеч. балки таврового профиля (рисунок)

с – проекция опасного накл. сеч.; с₀ – проекция опасной накл. трещины; Q – попер. сила от внешней нагр.: Q=Qmax-q*c; Qb – попер. усилие в сжатом Б; s – шаг попер. ар-ры.

Усл. прочности из усл. равновесия: ΣNверт=0: Q≤Qb+ΣRsw*Asw+ΣRsw*As,inc*sinα, Qb=(φb2*(1+φn+φf)*Rbt*b*h₀²)/c, где φb2 – зависит от вида Б (2,0 для тяжелого); φf – учитывает влияние сжатых полок.

Условие расчета: 1+φn+φf≤1,5

ΣRsw *Asw и ΣRsw*As,inc*sinα – суммарные усилия в хомутах и накл. стержнях, Rsw – расч. сопр. попер. ар-ры раст. ΣRsw *Asw=Qsw=q_sw*c_o.

Усл. для хомутов: q_sw≥(φb3*(1+φn+φf)*Rbt*b)/2, где φb3 – зависит от вида Б (0,6 для тяжелого).

Усл. для элементов с попер. и прод. арм-ем: Q≤Qb+Qsw.

Опр. длины проекции опасной накл. трещины: c₀=((φb2*(1+φn+φf)*Rbt*b*h₀²)/q_sw)^0.5, h0≤c≤2h0.

Расчет попер. ар-ры не треб при усл.: Qmax≤Qbmin=φb3*(1+φn)Rbt*b/h0).