10Интерполяция с помощью многочлена Лагранжа. Суть метода, формулы, достоинства и недостатки, примеры для двух узлов интерполяции.

Один из подходов к задаче интерполяции — метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Легко видеть, сто функция 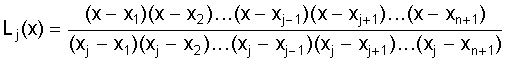                         является требуемым многочленом степени n; он равен 1, если x=x_j и 0, когда x=x_i, i¹j. Многочлен L_j(x)×y_j принимает значенияy_i в i-й узловой точке и равен 0 во всех других узлах. Из этого следует, что 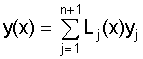  есть многочлен степени n, проходящий через n+1 точку (x_i, y_i).

11Интерполяционные формулы Ньютона. Сплайн-интерполяция. Сравнение методов интерполяции.

Интерполирование многочленом Лагранжа или Ньютона на всём отрезке с использованием большого числа узлов интерполяции >10 часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений.

Для того, чтобы избежать больших погрешностей, весь отрезок разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию многочленом невысокой степени ( так называемая кусочно-полиноминальная интерполяция ).

Один из способов кусочно-полиномиальной интерполяции является интерполяция с помощью сплайн – функций.

Слово "сплайн" происходит от английского spline и означает гибкую линейку, используемую для проведения гладких кривых через заданные точки плоскости.

Его поведение между этими точками определяется упругостью этого стержня.

Преимуществом сплайнов перед обычной интерполяцией является

1. их сходимость

2. устойчивость

процесса вычислений.

Рассмотрим способ построения кубического сплайна, интерполирующего заданную функцию на .

Итак, пусть на введена сетка функция задана своими значениями в узлах сетки .

Сплайном, соответствующим данной функции и данным узлом сетки называется функция , удовлетворяющая следующим условиям:

1) На каждом частичном отрезке функция является многочленом 3 степени.

2. Функция а так же её 1и 2 производная непрерывны на .

3. Функция удовлетворяет условиям интерполяции

На каждом из отрезков ищем в виде многочлена 3 степени:

;

где - коэффициенты, подлежащие определению. Поясним смысл введенных коэффициентов для этого вычислим производные этого многочлена:

поэтому

Из условий интерполяции получаем, что .

Функция непрерывна на поэтому

отсюда получаем уравнение:

Условия непрерывности первой производной

приводят к уравнениям .

Из условий непрерывности второй производной получаем уравнения:

Получили систему уравнений относительно неизвестных ,где .

Два недостающих уравнения получают, задавая те или иные граничные условия для . Предположим, например, что . Тогда естественно потребовать, чтобы и сплайн - функция . Отсюда получаем:

; , т.е. ;

Таким образом приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна.

Убедимся в том , что система имеет единственное решение. Исключим из переменные и и получим систему, содержащую только .

Для этого рассмотрим два соседних уравнения вида ( 3 )

и вычтем из второго уравнения первое. Получим :

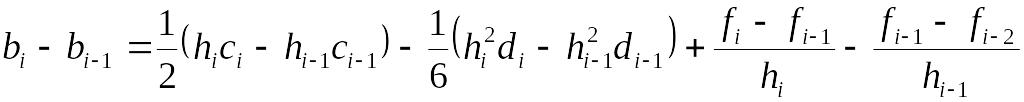
Подставляя найденное выражение для в правую часть уравнения ( 2 ), получим

Из уравнения ( 1 ) получаем: ,

и подставляя эти выражения в преобразованные 2-ые уравнения, приходим к уравнению:

.

Окончательно для определения коэффициентов получаем систему уравнений

В силу диагонального преобладания система имеет единственное решение, так как матрица системы трехдиагональная, решение легко найти методом прогонки. По найденным коэффициентам коэффициенты и определяются по формулам: