
- •3. Анықталған интегралдың қасиеттері. Анықталған интегралдың жалпы бағалануы, монотомдылығы.
- •4. Орта мән туралы 1-теорема
- •5. Ньютон Лейбниц формуласы. Жоғарғы шегі айнымалы болатын интеграл.
- •Айнымалыны ауыстыру әдісі. Бөліктеп, бөлшектеп интегралдау. Мысал:
- •10. Көп айнымалы функцияның туындылары мен дифференциалдары
- •11. Бағыт бойынша туынды. Жоғарғы ретті дифференциалдау
- •12.Тейлор формуласы
- •Көп айнымалы функцияның экстремумы.
- •Сандық қатарлар. Қатарлар жинақтылығы. Коши критерий.
- •15. Қатар жинақтылығының қажетті шарты. Қатардың қалдығы.
- •16.Мүшелері теріс емес қатарлар. Салыстыру белгілері
- •17.Даламбер белгісі. Коши белгісі. Мысал:
- •18.Абсолют және шартты жинақталатын қатарлар.
- •19. Раабе белгісі. Гаусс белгісі. Мысал
- •20. Абель теңсіздігі. Дирихле белгісі. Абель белгісі. Мысал
- •23. Функционалдық тізбектер мен қатарларды мүшелеп нтегралдау.
- •24)Функционалдық тізбектер мен қатарларды мүшелеп дифференциалдау.
- •29)Қисық сызықты интегралдар
24)Функционалдық тізбектер мен қатарларды мүшелеп дифференциалдау.
Теорема. Егер [a, b] кесіндісінде әрбір fn(x) функциясының fn’(x) туындысы бар және бұл {fn’(x)} туындылар тізбегі [a, b] кесіндісінде бірқалыпты жинақты, ал {fn(x)} тізбегі [a, b] кесіндісінің ең болмағанда бір x0 нүктесінде жинақты болса, онда {fn(x)} тізбегі белгілі бір f(x) шектік функциясына бүкіл [a, b] кесіндісінде бірқалыпты жинақты әрі бұл тізбекті мүшелеп дифференциялдауға болады, яғни бүкіл [a, b] кесіндісінде f(x) шектік функциясының {fn(x)} функциялық тізбегінің шегі болатын f ’(x) туындысы бар.
Дәлелдеуі.
Ең алдымен {fn(x)}
тізбегінің [a, b] сегментінде бірқалыпты
жинақты екенін дәлелдейік. {fn(x)}
тізбегінің х0
[a
,b] нүктесінде жинақтылығы мен {fn’(x)}
тізбегінің [a, b] кесіндісінің бірқалыпты
жинақтылығынан
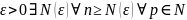 ( |fn+p(x0)
–fn
(x0)
|)<
⋀
( | f ‘n+
p(x)
–f ’n
(x)
| <
( |fn+p(x0)
–fn
(x0)
|)<
⋀
( | f ‘n+
p(x)
–f ’n
(x)
| <
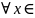 [
a ,b] ) (1) Айталық
х [ a ,b] кесіндісінің кез келген нүктесі
болсын. Онда барлық n, p
[
a ,b] ) (1) Айталық
х [ a ,b] кесіндісінің кез келген нүктесі
болсын. Онда барлық n, p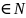 нөмірлерінде fn+p(t)
–fn
(t)
функциясы [ x0
,
x] кесіндісінде Лагранж теоремасының
барлық шарттарын қанағаттандырады ,
сондықтан [ x0
,
x] кесіндісінен
нөмірлерінде fn+p(t)
–fn
(t)
функциясы [ x0
,
x] кесіндісінде Лагранж теоремасының
барлық шарттарын қанағаттандырады ,
сондықтан [ x0
,
x] кесіндісінен
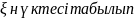
[
fn+p(x)
–fn
(x)
] – [ fn+p(x0)
–fn
(x0)
] = [f n+
p’(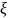 )
–f n
‘(
)](x-x0)
теңдігі орындалады. Енді |x-x0|
)
–f n
‘(
)](x-x0)
теңдігі орындалады. Енді |x-x0|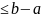 болғандықтан, мұнан және ( 1) теңсізхдіктерден
болғандықтан, мұнан және ( 1) теңсізхдіктерден
|fn+p(x)
–fn
(x)|<
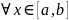
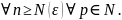 Ал бұл Коши критерийі бойынша {fn(x)}
тізбегінің [ a ,b] кесіндісінде бірқалыпты
жинақты екенін көрсетеді.Оның шектік
функциясын f(x) арқылы белгілейік. Енді
бізге
Ал бұл Коши критерийі бойынша {fn(x)}
тізбегінің [ a ,b] кесіндісінде бірқалыпты
жинақты екенін көрсетеді.Оның шектік
функциясын f(x) арқылы белгілейік. Енді
бізге
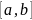 кесіндісінің кез келген х0
нүктесінде f(x) функциясының туындысының
бар және ол туынды {f n
‘(x)}
тізбегінің шегі екенін ғана көрсету
керек. Ол үшін x0
нүктесінің
кесіндісінің кез келген х0
нүктесінде f(x) функциясының туындысының
бар және ол туынды {f n
‘(x)}
тізбегінің шегі екенін ғана көрсету
керек. Ол үшін x0
нүктесінің
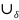 (x0
)⊂[a,
b] болатындай
(x0
)⊂[a,
b] болатындай
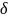 маңайын аламыз ( егер x0
шеткі
нүкте, мысалы
x0=a
болса , онда маңай үшін [a, a+
маңайын аламыз ( егер x0
шеткі
нүкте, мысалы
x0=a
болса , онда маңай үшін [a, a+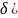 жарты
маңайын аламыз). {
x
} арқылы 0<
жарты
маңайын аламыз). {
x
} арқылы 0<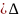 x
|<
( егер a<x
0<b
болса), 0<
x
<
(егер x0=a
болса ), -
<
x
<
x
|<
( егер a<x
0<b
болса), 0<
x
<
(егер x0=a
болса ), -
<
x
<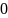 (егер x0=l
болса) шарттарын қанағаттандыратын
барлық
x
сандар жиынын белгілейміз және
x
аргументінің функциялар тізбегі
(егер x0=l
болса) шарттарын қанағаттандыратын
барлық
x
сандар жиынын белгілейміз және
x
аргументінің функциялар тізбегі
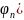 x)
=
x)
=
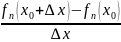 осы {
x
} жиынында бірқалыпты жинақталатынын
дәлелдейміз. {f n
‘(x)}
тізбегінің бірқалыпты жинақтылығынан
осы {
x
} жиынында бірқалыпты жинақталатынын
дәлелдейміз. {f n
‘(x)}
тізбегінің бірқалыпты жинақтылығынан
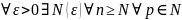 (
|f ’n+p
(x) –f ‘n
(x)
|<
)
(
|f ’n+p
(x) –f ‘n
(x)
|<
)
{
x
} жиынынан
x
алып [ x0
,
x0
+
x
] сегментінде fn+p(t)
–fn
(t)
функциясына Лагранж теоремасын
қолдансақ,
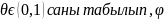 n+p(
x)
–
n+p(
x)
–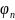 (
x)=
(
x)=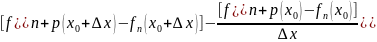 = f n+p’(x0+
= f n+p’(x0+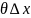 )
–fn’
(x0+
)
)
–fn’
(x0+
)
бұған
(2) қолдансақ |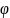 n+p(
x)
–
(
x)|
<
n+p(
x)
–
(
x)|
<
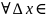 {
x
}
{
x
}
Сонымен
Коши критерийі бойынша, бұл
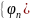 x)
} тізбегі {
x
} жиынында бірқалыпты жинақты. Ал бұл
x)}
тізбегіне
x
=0 нүктесінде мүшелеп шекке көшу теоремасын
пайдалануға мүмкіндік береді. Демек
x)}
тізбегінің шектік функциясы болатын
x)
} тізбегі {
x
} жиынында бірқалыпты жинақты. Ал бұл
x)}
тізбегіне
x
=0 нүктесінде мүшелеп шекке көшу теоремасын
пайдалануға мүмкіндік береді. Демек
x)}
тізбегінің шектік функциясы болатын
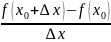 Функциясының
x
нөлге ұмтылғанда шектік мәні бар және
Функциясының
x
нөлге ұмтылғанда шектік мәні бар және
 =
=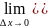 =
=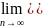 =
=
=
=
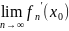
Бұл
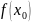 функциясының
функциясының
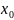 нүктесінде туындысы бар және ол
екенін дәлелдейді. Теорема дәлелденді.
нүктесінде туындысы бар және ол
екенін дәлелдейді. Теорема дәлелденді.
26. Дәрежелік қатарды мүшелеп интегралдау және дифференциалдау.
1-теорема.
Егер мына қатардың a0+
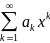 =
a0+a1x+
a 2x2
+……+
a n
x
n
+….
(1)
=
a0+a1x+
a 2x2
+……+
a n
x
n
+….
(1)
Жинақталу радиусы R, ал х айнымалысы |x|< R шартын қанағаттандырса, онда (1) қатарды [0, x] кесіндісінде мүшелепинтегралдауға болады және мүшелеп интегралдаудан шыққан қатардың да жинақталу радиусы бастапқы қатар жинақталу радиусына тең.
Дәлелдеу. |x|< R болса, онда | x|<r <R шартын қанағаттандыратын r табылады. Ал
қатар [-r , r] кесіндісінде бірқалыпты жинақты, демек, [0, x] кесіндісінде де бірқалыпты жинақты. Онда бұл қатарды [0 , x] кесіндісінде мүшелеп интегралдауға болады және оны интегралдаудан
a0x
+
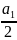 x2
+
…. +
x2
+
…. +
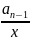 x
n
+ …. Дәрежелік қатарын аламыз. Мұның
жинақталу радиусы
x
n
+ …. Дәрежелік қатарын аламыз. Мұның
жинақталу радиусы
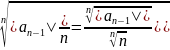 (
2) Тізбегінің жоғарғы шегінің кері
шамасына тең. Ал (2) тізбектің жоғарғы
шегі мына {
(
2) Тізбегінің жоғарғы шегінің кері
шамасына тең. Ал (2) тізбектің жоғарғы
шегі мына {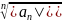 }, n=1,2..... тізбек шегіне тең, өйткені
}, n=1,2..... тізбек шегіне тең, өйткені
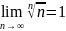 ,
,
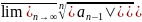 =
=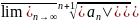 =
=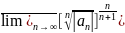 = =
= =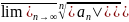
Теорема дәлелденді. 2-теорема. (1) дәрежелік қатарды жинақталу аралығында мүшелеп дифференциалдауға болады. Мүшелеп дифференциалаудан шыққан қатардың жинақталу радиусы бастапқы қатардың жинақталу радиусына тең. Дәлелдеу. (1) қатарды мүшелеп дифференциалаудан шыққан a1+2a2x+…..+ nanxn-1+ (n+1) an+1 x n +…...
қатардың
жинақталу радиусы
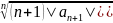 Тізбегінің жоғарғы шегінің кері шамасына
тең. Ал ( 3) тізбектің жоғарғы шегі келесі
тізбектің жоғарғы шегіне тең {
}, n=1,2..... , өйткені
Тізбегінің жоғарғы шегінің кері шамасына
тең. Ал ( 3) тізбектің жоғарғы шегі келесі
тізбектің жоғарғы шегіне тең {
}, n=1,2..... , өйткені
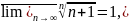
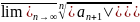 =
=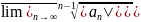 =
=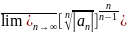 = =
.
= =
.
Теорема дәлелденді.
