
- •3. Анықталған интегралдың қасиеттері. Анықталған интегралдың жалпы бағалануы, монотомдылығы.
- •4. Орта мән туралы 1-теорема
- •5. Ньютон Лейбниц формуласы. Жоғарғы шегі айнымалы болатын интеграл.
- •Айнымалыны ауыстыру әдісі. Бөліктеп, бөлшектеп интегралдау. Мысал:
- •10. Көп айнымалы функцияның туындылары мен дифференциалдары
- •11. Бағыт бойынша туынды. Жоғарғы ретті дифференциалдау
- •12.Тейлор формуласы
- •Көп айнымалы функцияның экстремумы.
- •Сандық қатарлар. Қатарлар жинақтылығы. Коши критерий.
- •15. Қатар жинақтылығының қажетті шарты. Қатардың қалдығы.
- •16.Мүшелері теріс емес қатарлар. Салыстыру белгілері
- •17.Даламбер белгісі. Коши белгісі. Мысал:
- •18.Абсолют және шартты жинақталатын қатарлар.
- •19. Раабе белгісі. Гаусс белгісі. Мысал
- •20. Абель теңсіздігі. Дирихле белгісі. Абель белгісі. Мысал
- •23. Функционалдық тізбектер мен қатарларды мүшелеп нтегралдау.
- •24)Функционалдық тізбектер мен қатарларды мүшелеп дифференциалдау.
- •29)Қисық сызықты интегралдар
20. Абель теңсіздігі. Дирихле белгісі. Абель белгісі. Мысал
Абель
белгісі.1-теорема. Егер {Un}
тізбегі монотонды және шектеулі , ал
Егер
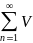 n
қатары
жинақты болса , онда (1) қатар жинақты.
Д/у: Теорема шартынан М
n
қатары
жинақты болса , онда (1) қатар жинақты.
Д/у: Теорема шартынан М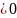 саны табылып , барлық n=1,2,… үшін | U n
|
Mтеңсіздігі
орындалатыны айқын. Ал
n
қатарының
жинақтылығынан :
саны табылып , барлық n=1,2,… үшін | U n
|
Mтеңсіздігі
орындалатыны айқын. Ал
n
қатарының
жинақтылығынан :
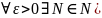 n+k
|
n+k
|
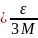 )
. Сонымен бірге Абель теңсіздігінен
)
. Сонымен бірге Абель теңсіздігінен
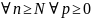
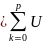 n+kVn+k|
(|Un
|+
2|Un+p|
)
.
n+kVn+k|
(|Un
|+
2|Un+p|
)
.
Сонда , Коши критерийі бойынша , бұдан (1) қатар жинақтылығы шығады.
Ескерту:
Абель белгісін Дирихле белгісінің
салдары ретінде де қарауға болады.
Шынында да ,{Un}
тізбегінің монотондығы мен шектеулілігінен
U=
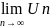 шегі
бар , демек ,Wn
= Un
–
U тізбегі монотонды нөлге ұмтылады. Ал
шегі
бар , демек ,Wn
= Un
–
U тізбегі монотонды нөлге ұмтылады. Ал
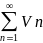 қатарының
дербес қосындылары шегі шектеулі ,
себебі бұл қатар жинақты. Сондықтан
Дирихле белгісі бойынша
қатарының
дербес қосындылары шегі шектеулі ,
себебі бұл қатар жинақты. Сондықтан
Дирихле белгісі бойынша
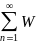 nVn
қатары
жинақты. Бірақ WV = UnVn-Un
Vn
және
Vn=
nVn
қатары
жинақты. Бірақ WV = UnVn-Un
Vn
және
Vn=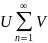 nқатары
жинақты. Сонда екі жинақталатын қатар
қосындысы ретінде
nқатары
жинақты. Сонда екі жинақталатын қатар
қосындысы ретінде
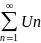 Vn=
nVn
+
nқатары
жинақты.
Vn=
nVn
+
nқатары
жинақты.
Дирихле
белгісі. Егер
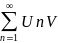 n
(1)
Қатарында {Un}
тізбегі нөлге монотонды ұмтылса , ал
n
қатарының
{Вn}
дербес қосындылар тізбегі шектеулі
болса , онда (1) қатар жинақты. Д/у:
{Вn}
тізбегінің шектеулігінен M>0 саны
табылып , барлық n=1.2…. үшін |Bn
|
n
(1)
Қатарында {Un}
тізбегі нөлге монотонды ұмтылса , ал
n
қатарының
{Вn}
дербес қосындылар тізбегі шектеулі
болса , онда (1) қатар жинақты. Д/у:
{Вn}
тізбегінің шектеулігінен M>0 саны
табылып , барлық n=1.2…. үшін |Bn
|
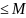 теңсіздігі
орындалады. Сонда
теңсіздігі
орындалады. Сонда I
|
= |Bn+p
–
B n-1
|
|Bn+p|
+|
B n-1
|
2M
(1) Ал
I
|
= |Bn+p
–
B n-1
|
|Bn+p|
+|
B n-1
|
2M
(1) Ал
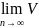 n
=0
шартынан : кез келген
саны үшін N – нөмірі табылып, барлық
n
=0
шартынан : кез келген
саны үшін N – нөмірі табылып, барлық
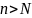 үшін | U n
|
үшін | U n
|
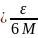 (2) Теңсіздігі орындалады. Енді
үшін
(2) Теңсіздігі орындалады. Енді
үшін
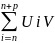 i
қосындысына
(1), (2)- теңсіздіктерін ескеріп , Абель
теңсіздігін қолдансақ ,
i
қосындысына
(1), (2)- теңсіздіктерін ескеріп , Абель
теңсіздігін қолдансақ ,
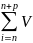 IBi
2M( |Un|
+2|
U n+p
|
теңсіздігін аламыз. Мұнан Коши критерийі
бойынша (1) қатар жинақсыздығы шығады.
IBi
2M( |Un|
+2|
U n+p
|
теңсіздігін аламыз. Мұнан Коши критерийі
бойынша (1) қатар жинақсыздығы шығады.
23. Функционалдық тізбектер мен қатарларды мүшелеп нтегралдау.
Теорема.
Егер [a , b] кесіндісінде {fn(x)}
функциялық тізбек f(x) шектік функцияға
бірқалыпты жинақты және тізбектің әрбір
fn(x)
мүшесі [a
, b] кесіндісінде интегралданатын болса,
онда f(x)
шектік функция да [a
,b] кесіндісінде интегралданады және
тізбекті [a ,b] кесіндісінде мүшелеп
интегралдауға болады, яғни
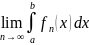 Шегі бар және ол
Шегі бар және ол
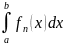 интегралына тең. Дәлелдеуі.
{fn(x)}
тізбегі [a
,b] кесіндісінде f(x)
функциясына бірқалыпты жинақты
болғандықтан, кез-келген
санына сәйкес N(
)
нөмірі табылып, барлық n
N(
)
және барлық х
интегралына тең. Дәлелдеуі.
{fn(x)}
тізбегі [a
,b] кесіндісінде f(x)
функциясына бірқалыпты жинақты
болғандықтан, кез-келген
санына сәйкес N(
)
нөмірі табылып, барлық n
N(
)
және барлық х
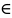 [a
,b] үшін |fn(x)
– f(x)|<
[a
,b] үшін |fn(x)
– f(x)|<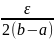 (1) Енді f(x)
шектік функциясының
[a , b] кесіндісінде интегралданатынын
көрсетейік. [a , b] кесіндісінде
a=x0<x1<…..<xm=b
нүктелері арқылы бөлшектеу жасап Wk(f)
Және Wk(fn)
символдары арқылы f(x)
және
fn(x)
функцияларының [xk-1,
xk]
k=1,….,m дербес сегменттеріндегі
сәйкестерін белгілейік. Егер x’, x’’
[a
,b] болса, онда |f(x’)-f(x’’)|
|f(x’)-fn(x’)|+
+ |fn(x’)-fn(x’’)|+
|fn(x’’)-f(x’’)|.
(2) Ал (1) бойынша
(1) Енді f(x)
шектік функциясының
[a , b] кесіндісінде интегралданатынын
көрсетейік. [a , b] кесіндісінде
a=x0<x1<…..<xm=b
нүктелері арқылы бөлшектеу жасап Wk(f)
Және Wk(fn)
символдары арқылы f(x)
және
fn(x)
функцияларының [xk-1,
xk]
k=1,….,m дербес сегменттеріндегі
сәйкестерін белгілейік. Егер x’, x’’
[a
,b] болса, онда |f(x’)-f(x’’)|
|f(x’)-fn(x’)|+
+ |fn(x’)-fn(x’’)|+
|fn(x’’)-f(x’’)|.
(2) Ал (1) бойынша
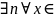 [a
,b] |f(x’)-fn(x’)|+
|fn(x’’)-f(x’’)|<
[a
,b] |f(x’)-fn(x’)|+
|fn(x’’)-f(x’’)|<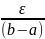 , Демек, (2) бойынша |f(x’)-f(x’’)|
|fn(x’)-fn(x’’)|+
Мұнан және x’,
x’’ нүктелері кез келген болғандықтан,
таңдап алынған n үшін кез келген
саны мен әрбір k=1,….,m
нөміріне сәйкес
, Демек, (2) бойынша |f(x’)-f(x’’)|
|fn(x’)-fn(x’’)|+
Мұнан және x’,
x’’ нүктелері кез келген болғандықтан,
таңдап алынған n үшін кез келген
саны мен әрбір k=1,….,m
нөміріне сәйкес Wk(f)
Wk(fn)
+
(3) Біздің бөлшектеуімізге сәйкес f(x)
функциясының жоғарғы және төменгі
қосындыларын S
және
s, ал fn(x)
функциясының жоғарғы және төменгі
қосындыларына сәйкес Sn
және sn
арқылы
белгілейік.Сөйтіп (3) теңсіздікті к-ші
дербес сегмент
Wk(f)
Wk(fn)
+
(3) Біздің бөлшектеуімізге сәйкес f(x)
функциясының жоғарғы және төменгі
қосындыларын S
және
s, ал fn(x)
функциясының жоғарғы және төменгі
қосындыларына сәйкес Sn
және sn
арқылы
белгілейік.Сөйтіп (3) теңсіздікті к-ші
дербес сегмент
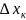 ұзындығына көбейтіп, барлық k=1,….,m,
арқылы қосындыласақ,
ұзындығына көбейтіп, барлық k=1,….,m,
арқылы қосындыласақ,
S-
s
Sn
- sn
+
(4) Теңсіздігін
аламыз. Теорема шарты бойынша [a , b]
кесіндісінде fn(x)
интегралданады, яғни Sn
- sn
<
, онда (4) теңсіздіктен
S- s< ,
демек, [a , b] кесіндісінде f(x) функциясы
интегралданады. |
–
,
демек, [a , b] кесіндісінде f(x) функциясы
интегралданады. |
–
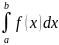 |=
|=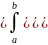 –f(x)]dx|
–f(x)]dx|
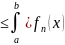 –f(x)|dx
–f(x)|dx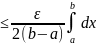 =
=
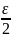 <
,
<
,
 n
N(
)
аламыз.Бұдан
шегінің бар жәнә оның
интегралыңа тең екенін аламыз.Теорема
дәлелдеденді.
n
N(
)
аламыз.Бұдан
шегінің бар жәнә оның
интегралыңа тең екенін аламыз.Теорема
дәлелдеденді.
Бұл теореманы функциялық қатар үшін былай айтамыз. Егер функциялық қатар өзінің S(x) қосындысына [a, b] кесіндісінде бірқалыпты жинақты және оның әрбір Uk(x) мүшесі [a, b] кесіндісінде интегралданатын болса, онда S(x) қосындысы [a, b] кесіндісінде интегралданады, әрі қатарды [a, b] кесіндісінде мүшелеп интегралдауға болады, яғни
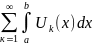 жинақты
және оның қосындысы
жинақты
және оның қосындысы
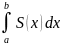 .
.
