15. Қатар жинақтылығының қажетті шарты. Қатардың қалдығы.
Теорема 1.Қатардың жинақтылығының қажетті шарты.
Берілген шектеусіз сандар тізбегі үшін:
(1)
өрнегі сандық қатар деп аталады, мұндағы сандары – қатардың мүшелері.
саны қатардың бөлік қосындысы деп аталады.
(1) қатары жинақты болуы үшін болуы қажетті.
Мысалы:.
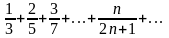қатары жинақсыз, себебі қатардың
жинақтылығының қажетті шарты орындалмайды:
.
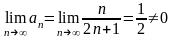болу шартынан қатардың жинақты екені шықпайды.
Теорема. Егер 
қатар
жинақты болса 
Un=0
болады.
Бұл
шарт жеткілікті шарт бола алмайды,
мысалы 
гармоникалық
қатар деп аталатын қатар жинақты емес
екендігі белгілі.(
-
қажетті шарт орындалады.)
(1) қатардың алғашқы n мүшелерін лақтырып тастағаннан пайда болған қатарын (1) қатардың қалдығы немесе (1) қатардың n-ші қалдығы деп атайды.
16.Мүшелері теріс емес қатарлар. Салыстыру белгілері
1-
Теорема. Айталық
және 
мүшелері теріс емес екі қатары беріліп,
барлық n нөмірлері үшін 
(1) теңсіздігі орындалсын. Онда
қатарының жинақтылығынан
қатарының жинақтылығы, ал
қатарының жинақсыздығынан
қатарының жинақсыздығы шығады. Дәлелдеу
және
қатарларының n-ші дербес қосындыларын
сәйкес 
арқылы белгілейік. Онда
теңсіздіктен 
(2) теңсіздігі шығады.
қатары жинақты және Q оның қосындысы
болса, онда 
Q теңсіздігін , ал
теңсіздіктен 
(3) аламыз, яғни
қатарының дербес қосындылар тізбегі
жоғарыдан Q санымен шектелген, демек,
қатары жинақты.Енді теореманың екінші
жартысын дәлелдейік.
қатарының {
}
дербес қосындылар тізбегінің
шектеусіздігінен
қатарының дербес қосындылар тізбегі
{
}
шектеусіздігі шығады. 1-
ескерту. Бұл
теоремада
теңсіздік барлық n нөмірлері үшін емес
тек белгілі бір нөмірден бастап орындалса
болғаны, өйткені саны ақырлы мүшелерін
лақтырып тастағаннан қатар жинақтылығы
өзгермейді.Салдар
Егер
мүшелері теріс емес , ал
мүшелері қатаң оң қатарлар болып және
= L, L
0,
ақырлы шегі бар болса , онда
қатарының жинақтылығынан
қатарының жинақтылығы, ал
қатарының жинақсыздығынан
қатарының жинақсыздығы шығады. Дәлелдеу
Шек
анықтамасынан
= L дегеніміз анықтама бойынша: кез келген
>0
саны үшін N нөмірі табылып , n
N болғанда L-
= 
L+
,
яғни n
N болғанда 
(L+
)
теңсіздігі орынды.
2-
теорема. Айталық,
және
мүшелері қатаң оң екі қатар және барлық
n нөмірлері үшін 
(4) теңсіздігі орындалсын. Онда
қатарының жинақтылығынан
қатарының жинақтылығы, ал
қатарының жинақсыздығынан
қатарының жинақсыздығы шығады. Дәлелдеу
теңсіздікті n=1,2,…k-1 үшін жазсақ 
,
, .…, 
бұл теңсіздіктерді мүшелеп көбейтсек,
теңсіздігін
аламыз. Мұндағы 
= C көбейткіші оң және k-ден тәуелсіз
тұрақтыны анықтайтын болады.