
- •3. Анықталған интегралдың қасиеттері. Анықталған интегралдың жалпы бағалануы, монотомдылығы.
- •4. Орта мән туралы 1-теорема
- •5. Ньютон Лейбниц формуласы. Жоғарғы шегі айнымалы болатын интеграл.
- •Айнымалыны ауыстыру әдісі. Бөліктеп, бөлшектеп интегралдау. Мысал:
- •10. Көп айнымалы функцияның туындылары мен дифференциалдары
- •11. Бағыт бойынша туынды. Жоғарғы ретті дифференциалдау
- •12.Тейлор формуласы
- •Көп айнымалы функцияның экстремумы.
- •Сандық қатарлар. Қатарлар жинақтылығы. Коши критерий.
- •15. Қатар жинақтылығының қажетті шарты. Қатардың қалдығы.
- •16.Мүшелері теріс емес қатарлар. Салыстыру белгілері
- •17.Даламбер белгісі. Коши белгісі. Мысал:
- •18.Абсолют және шартты жинақталатын қатарлар.
- •19. Раабе белгісі. Гаусс белгісі. Мысал
- •20. Абель теңсіздігі. Дирихле белгісі. Абель белгісі. Мысал
- •23. Функционалдық тізбектер мен қатарларды мүшелеп нтегралдау.
- •24)Функционалдық тізбектер мен қатарларды мүшелеп дифференциалдау.
- •29)Қисық сызықты интегралдар
Көп айнымалы функцияның экстремумы.
Экстремум анықтамасы. Қажетті шарт. f сандық функциясы E⊂Rn жиынында анықталсын. Егер, біріншіден, а нүктесі Е жиынының ішкі нүктесі болса, екіншіден,
Vв (a) ⊂E кірістіруі орындалатындай қайсыбір δ оң саны мен әрбір х∈Vв(а) үшін f(x)≤f(a)(f(x)≥f(a)) теңсіздігі орындлса, онда а нүктесін f(x) функциясы локальді максимум (локальді минимум) мәнін қабылдайтын нүкте, не қысқаша а- локальді максимум (локальді минимум) нүктесі деп атайды.
Бір айнымалы жағдайындағы сияқты, локальді максимум (локальді минимум) анықтамасында f(a) мәні бір ғана а нүктесінде қабылданса, яғни х≠а, х∈Vв(а) болғанда f(x)<f(a) (f(x)>f(a)) болса, онда а нүктесі f функциясының локальді қатаң максимум (локальді қатаң минимум) нүктесі деп аталады.
локальді максимум мен локальді минимумді локальді экстремум деп атайды.
Егер а нүктесі f функциясы үшін локальді экстремум нүктесі болып, f функциясының а нүктесінде барлық дербес туындылары бар болса, онда сол дербес туындылар міндетті түрде нольге тең болады.
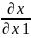 (a)=0,
…,
(a)=0,
…,
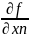 (a)=0.
(a)=0.
Сандық қатарлар. Қатарлар жинақтылығы. Коши критерий.
Анықтама
1. Берілген
шектеусіз
сандар
тізбегі
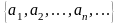 үшін:
үшін:
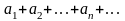 (1)
(1)
өрнегі
сандық қатар деп аталады, мұндағы
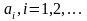 сандары – қатардың мүшелері.
сандары – қатардың мүшелері.
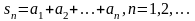 саны
қатардың бөлік қосындысы деп аталады.
саны
қатардың бөлік қосындысы деп аталады.
Анықтама
2.
Егер
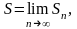 шегі табылатын болса, онда
шегі табылатын болса, онда
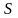 (1) қатарының қосындысы деп аталады.
(1) қатарының қосындысы деп аталады.
Анықтама
3.
Қатар жинақты деп аталады, егер
тұрақты санға тең болса, кері жағдайда,
яғни,
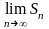 шегі шексіздікке тең болса немесе
табылмаса, онда қатар жинақсыз деп
аталады.
шегі шексіздікке тең болса немесе
табылмаса, онда қатар жинақсыз деп
аталады.
Теорема
1.Қатардың жинақтылығының қажетті шарты.
(1)
қатары жинақты болуы үшін
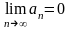 болуы қажетті.
болуы қажетті.
Теорема.
Даламбер белгісі (Коши).
Егер
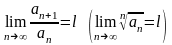 ,
мұндағы
,
мұндағы
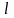 -ақырлы
сан болса, онда:
-ақырлы
сан болса, онда:
а)
егер
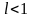 болса, онда (1)
қатары жинақты,
болса, онда (1)
қатары жинақты,
б)
егер
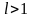 болса,
(1)
қатары жинақсыз,
болса,
(1)
қатары жинақсыз,
в)
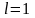 қатардың жинақтылығы туралы сұрақ
ашық қалады.
қатардың жинақтылығы туралы сұрақ
ашық қалады.
Теорема.
Кошидің интегралдық белгісі.
Қандай да бір
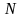 нөмірінен бастап
нөмірінен бастап
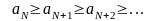 теңсіздігі орындалсын және
функциясы мынадай үзіліссіз өспелі
емес функция болсын:
теңсіздігі орындалсын және
функциясы мынадай үзіліссіз өспелі
емес функция болсын:
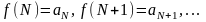 .
Онда, егер
.
Онда, егер
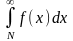 жинақты (жинақсыз) болса, онда (1) қатары
жинақты (жинақсыз).
жинақты (жинақсыз) болса, онда (1) қатары
жинақты (жинақсыз).
Коши
критерийі деп аталатын мына негізгі
екі теореманы келтірейік. 1-теорема.
{fn(x)}
функциялық тізбегінің D аймағында
белгілі бір шектік функцияға бірқалыпты
жинақталуы үшін кез келген
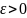 санына
сәйкес
санына
сәйкес
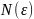 нөмірі
табылып
нөмірі
табылып
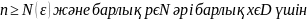
|Fn+p(x)
– fn(x)|
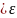 (1) Теңсіздігінің
орындалуы қажетті және жеткілікті.
(1) Теңсіздігінің
орындалуы қажетті және жеткілікті.
2-теорема:
D аймағында
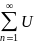 k
(x)
(2)функциялық
қатарының белгілі бір қосындыға
бірқалыпты жинақталуы үшін кез келген
k
(x)
(2)функциялық
қатарының белгілі бір қосындыға
бірқалыпты жинақталуы үшін кез келген
 нөмірі
табылып , барлық
нөмірі
табылып , барлық

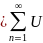 k
(x)
|
(3) теңсіздігінің орындалуы қажетті
және жеткілікті. Ескерту: 2- теорема
1- теореманың салдары , өйткені (3)
теңсіздіктің сол жағындағы иодуль
астында (2) қатар дербес қосындыларының
Sn+p
(x)
– Sn
(x)
айырымы тұр. Сондықтан 1-теореманығана
дәлелдейміз. Д/у: Қажеттілігі. Айталық
{fn(x)}
тізбегі D жиынында f(x)
шектік функцияға бірқалыпты жинақты
болсын. Онда
k
(x)
|
(3) теңсіздігінің орындалуы қажетті
және жеткілікті. Ескерту: 2- теорема
1- теореманың салдары , өйткені (3)
теңсіздіктің сол жағындағы иодуль
астында (2) қатар дербес қосындыларының
Sn+p
(x)
– Sn
(x)
айырымы тұр. Сондықтан 1-теореманығана
дәлелдейміз. Д/у: Қажеттілігі. Айталық
{fn(x)}
тізбегі D жиынында f(x)
шектік функцияға бірқалыпты жинақты
болсын. Онда
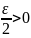 санын алып, оған сәйкес N нөмірін тауып
,
санын алып, оған сәйкес N нөмірін тауып
,
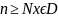 |Fn(x)
– f(x)|
|Fn(x)
– f(x)|
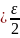 (4) орындалатынын көреміз. Мұнан
(4) орындалатынын көреміз. Мұнан
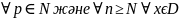 үшін |Fn+p(x)
– f(x)|
(5) Сонда (4) пен (5) тен|fn+p(x)
– fn(x)|
= |fn+p(x)
– f(x) + f(x) – fn(x)|
үшін |Fn+p(x)
– f(x)|
(5) Сонда (4) пен (5) тен|fn+p(x)
– fn(x)|
= |fn+p(x)
– f(x) + f(x) – fn(x)|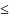 |fn+p(x)
– f(x)| + |fn(x)
– f(x)|
|fn+p(x)
– f(x)| + |fn(x)
– f(x)|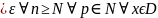 .
Жеткіліктілігі .Егер (1) орындалған
болса, онда мұнымен сандық тізбек үшін
Коши критерийінен D жиынның кез келген
х нүктесі үшін {fn(x)}
тізбегінің жинақтылығы мен f(x ) шектік
функциясының бар екені шығады. Ал
(1)теңсіздік
.
Жеткіліктілігі .Егер (1) орындалған
болса, онда мұнымен сандық тізбек үшін
Коши критерийінен D жиынның кез келген
х нүктесі үшін {fn(x)}
тізбегінің жинақтылығы мен f(x ) шектік
функциясының бар екені шығады. Ал
(1)теңсіздік
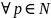 үшін
дұрыс болғандықтан , бұл теңсіздікте
р-ні шексіздікке ұмтылдырып , шекке
көшсек,
үшін
дұрыс болғандықтан , бұл теңсіздікте
р-ні шексіздікке ұмтылдырып , шекке
көшсек,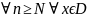 f(x)
– fn(x)|
f(x)
– fn(x)|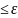 (6)
Теңсіздігін аламыз . Ал
кез келген болғандықтан жеткіліктілігі
дәлелденді.
(6)
Теңсіздігін аламыз . Ал
кез келген болғандықтан жеткіліктілігі
дәлелденді.
