10. Көп айнымалы функцияның туындылары мен дифференциалдары

Көп айнымалы функцияның дербес, толық өсімшелері және дербес туындылары. z = f (x, y) функциясымен анықталған бетті қарастырайық. Оны y= const жазықтығымен қияйық. Бұл жазықтықта у -тұрақты, х айнымалысына x өсімшесін берейік. Сонда х айнымалысы бойынша z функциясының _x z дербес өсімшесі

формуласымен анықталады.

Сол сияқты, егер z = f (x, y) функциясы үшін х – тұрақты болып, ал у айнымалысы бойынша у өсімшесін алса, онда у айнымалысы бойынша дербес өсімшесі

формуласымен анықталады.

Егер х және у айнымалылары бойынша x және у өсімшілерін қабылдаса, онда z функциясының толық өсімшесі

формуласымен анықталады.

z = f (x, y) функциясының х айнымалысы бойынша дербес туындысы деп

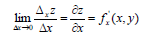шегін айтады.

z = f (x, y) функциясының у айнымалысы бойынша дербес туындысы деп

шегін айтады. Дербес туындыны есептеу ережесі: z = f (x, y) функциясының х айнымалысы бойынша дербес туындысын есептеу үшін z функциясының у – тұрақты деп алғандағы х бойынша туындысын есептеу керек, және, керісінше, у бойынша

дербес туындысын есептеу үшін z функциясының х – тұрақты деп алғандағы у бойынша туындысын есептейді.мысал:

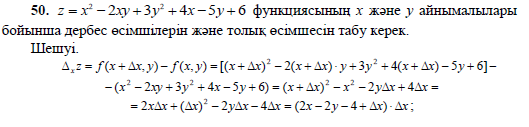
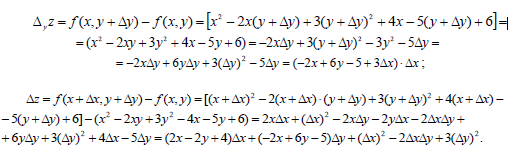
11. Бағыт бойынша туынды. Жоғарғы ретті дифференциалдау

Анықтама . z f (x, y) функциясының М(х, у) нүктесінде 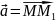векторының бағыты бойынша туындысы деп

шегін айтады, мұндағы .

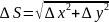Егер f (x, y) функциясы дифференциалданатын болса, онда бағыт бойынша туынды

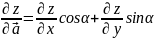(4.21)

формуласымен есептелінеді, мұндағы 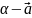векторы мен Ox осінің арасындағы бұрыш.

Үш айнымалы u f (x, y, z) функциясының бағыт бойынша туындысы

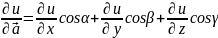
формуласымен есептелінеді, мұндағы cos, cos, cos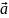 векторының бағытталған косинустары.

Жоғары ретті дифференциал. f(x) аралығында -рет дифференциалданатын функция, -тәуелсіз айнымалы. Онда функциясының нүктесіндегі бірінші дифференциалынан алынған дифференциал функциясының екінші дифференциалы деп аталады да арқылы белгіленеді, және

тең

функциясының - ретті дифференциалы деп функциясының - ретті дифференциалының дифференциалын айтады және оны келесі түрде белгілейді.

– ші ретті дифференциал үшін

теңдігі орындалады. – ші ретті дифференциалдар үшін келесі ережелер орындалады:

1)

2)

Екі функцияның көбейтіндісінің жоғарғы ретті туындысын қарастыралық.

және функциялары 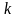– рет дифференциалданатын функциялар болсын, онда Лейбниц формуласы орынды:

; .

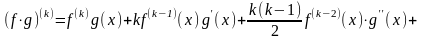
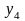
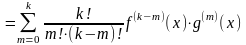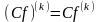12.Тейлор формуласы

функциясы X аралығында анықталып, нүктесінде туындылары бар болсын. функциясын жуықтау құралы ретінде сәйкес туындылары функциясының нүктесіндегі туындыларымен беттесетін дәрежелі көпмүшелікті, яғни

көпмүшелігін алайық. Ол функциясының нүктесіндегі Тейлор көпмүшелігі деп аталады.

Егер функциясы дәрежелі көпмүшелік болса, онда әрбір үшін

Басқа жағдайларда ондай теңдік орындалмауы мүмкін, демек қателік немесе қалдық мүше деп аталатын

функциясын қарауымыз қажетті.

функциясының анықтамасынан шығатын

формуласын Тейлор формуласы деп атайды.

болғанда, Тейлор формуласы мына түрге келеді:

Кейбір негізгі элементтар функциялардың Тейлор формуласымен жіктелуі:

Тейлор формуласын жуықтап есептеуге қолданады. Мысалы, е санын 0,001 дәлдігімен есептеу керек.

, . Тейлор формуласында тең деп аламыз,

, онда және қалдық мүше <0.001, деп алсақ, онда

Сонымен,