1. Анықталған интеграл. Дарбудың жоғарғы және төменгі қосындылары.

2. Интегралданатын функциялардың маңызды кластары.

3. Анықталған интегралдың қасиеттері. Анықталған интегралдың жалпы бағалауы. Монотондылығы.

4. Орта мән туралы бірінші теорема.

5. Ньютон Лейбниц формуласы. Жоғарғы шегі айнымалы болатын интеграл.

6. Айнымалыны ауыстыру әдісі. Бөліктеп, бөлшектеп интегралдау. Мысал:

7. Анықталған интегралдың кейбір қолданылулары.

8. R_n кеңістігіндегі көп айнымалы функциялардың шегі. Қайталамалы шектер.

9. Көп айнымалы функциялардың үзіліссіздігі. Мысал:

10. Көп айнымалй функциялардың туындысы. Мысал:

11. Бағыт бойынша туынды. Жоғарғы ретті дифференциялдар.

12. Тейлор формуласы.

13. Көп айнымалй функциялардың туындылары.

14. Сандық қатарлар. Қатар жинақтылығы. Коши крийтериі.

15. Қатар жинақтылығының қажетті шарты. Қатардың қалдығы.

16. Мүшелері теріс емес қатарлар. Олардың салыстыру белгілері.

17. Даламбер белгісі. Коши белгісі. Мысал:

18. Абсолют және шартты жинақталатын қатарлар.

19. Раабе белгісі. Гаусс белгісі. Мысал:

20. Абель теңсіздігі. Дирихле белгісі. Абель белгісі. Мысал:

21. Бірқалыпты жинақтылық. Коши крийтериі. Бірқалыпты жинақтылықтың жеткілікті белгілері.

22. Шекке мүшелеп көшу. Қатар қосындысы.

23. Функционалдық тізбектер мен қатарларды мүшелеп интегралдау.

24. Функционалдық тізбектер мен қатарларды мүшелеп дифференциалдау.

25. Дәрежелік қатарлар. Дәрежелік қатарлардың қосындысының үзіліссіздігі.

26. Дәрежелік қатарларды мүшелеп интегралдау.

27. Функцияны дәрежелік қатарға жіктеу.

28. Қос интеграл. Мысалдар:

29. Қисық сызықты интегралдар. Мысалдар:

30. Үш еселі интегралдар.

3. Анықталған интегралдың қасиеттері. Анықталған интегралдың жалпы бағалануы, монотомдылығы.

Анықталған интегралдың қасиеттері:

1. Жоғарғы және төменгі шектері өзара тең анықталған интеграл нөлге тең:

2. Шектерінің орнын ауыстырса, интегралдың таңбасы керіге өзгереді:

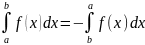
3. Интегралдау кесіндісін бөліктерге бөлуге болады:

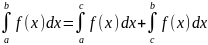
4. Анықталған интегралда айнымалыны ауыстырғанда интегралдау шекаралары да өзгереді:

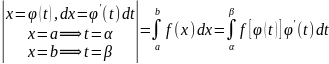
5. Анықталған интегралды бөлшектеп интегралдау: Егер 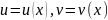екі дифференциалданатын функция болса,

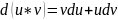
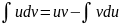анықталған интеграл үшін ⟹ .

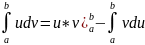- Ньютон-Лейбниц

Егер интегралдың қосындысы шегі болса, сонымен қатар ол шек шектеулі болса, онда ол шекті 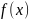функциясының а-дан b-ға дейінгі анықталған интегралы деп аталады.

Егер функциясы 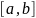кесіндісінде монотомды болса, онда ол осы кесіндіде Риман бойынша интегралданады.

4. Орта мән туралы 1-теорема

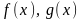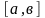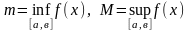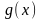1-теорема. Егер функциялары кесіндісінде интегралданса, ал және функциялары кесіндісінде теріс емес (немесе оң емес) болса, онда 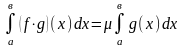(1) теңдігін қанағаттандыратын 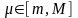саны табылады. Егер, сонымен бірге, 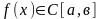болса, онда

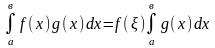(2) теңдігін қанағаттандыратын 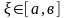табылады.

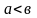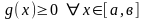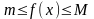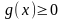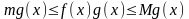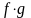Дәлелдеу. Интегралдау шектерін ауыстырғанда (1) теңдіктің екі жағын да таңбалары бірге өзгеретін болғандықтан, бұл теңдікті жағдайы үшін тексеру жеткілікті. Сонымен бірге, таңбасын өзгертсек, (1) теңдіктің екі жағының да таңбалары бірдей өзгеретін болғандықтан, жалпылығын шектемей-ақ, деп есептейміз. және болғандықтан, . Ал теорема шартынан және функциялары кесіндісінде интегралданатын функциялар және бұларға теңсіздікті пайдалансақ,

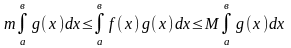(3) аламыз. Егер 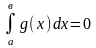болса, бұл теңсіздіктерден (1) орындалады. Ал, егер 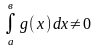болса, онда 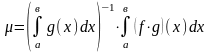деп, (3) теңсіздіктерден

екенін табамыз, ал бұл (1) теңдікпен тең мағыналы. (2) теңдік (1) теңдік пен 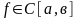функциясының аралық мәні туралы Коши теоремасынан шығады, өйткені болса, онда .

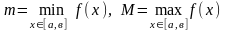5. Ньютон Лейбниц формуласы. Жоғарғы шегі айнымалы болатын интеграл.

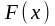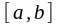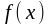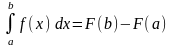Теорема. Егер функциясы аралығына функциясының алғашқы функциясы болса, онда . (1)

Бұл теңдік Ньютон-Лейбниц формуласы деп аталады.

Дәлелдемесі. функциясы -да функциясының алғашқы функцияларының бірі болсын. Жоғарыда айтылған б-ша кесіндісінде функциясының алғашқы функциясы болып табылатын мына 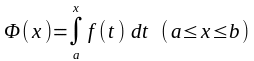функция болады.

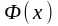пен бір ғана функциясының алғашқы функциялары болғандықтан, 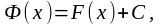яғни .

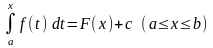Бұдан 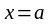болғанда теңдігі орындалады. Олай болса

.

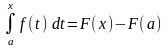Енді 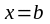деп алсақ, онда (1) формулаға келеміз.

Ньютон-Лейбниц формуласы анықталған интеграл мен алғашқы функцияның (анықталмаған интегралдың) байланысын көрсетеді. Сондықтан анықталған интегралдауды есептеуді анықталмаған интегралдарды есептеуге келтіреді, яғни бірінші теңдеуде қарастырылған анықталмаған интегралдарды есептеп шығару формулаларын пайдалануға мүмкіндік береді. Бұл формула интегралдық есептеудің негізгі формуласы деп те аталады.

Ньютон-Лейбниц формуласын есептеуге ыңғайлы болу үшін, оның оң жағын 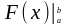символымен белгілейміз, яғни .

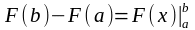Сонда, (1) формуласы мына түрде 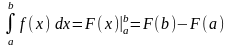жазылады.

Мысал-4. 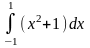интегралын есептеп табу керек.

Шешу: .

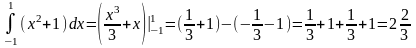Жоғарғы шегі айнымалы болатын интеграл

Анықтама: [a,b] кесіндісінде y= f(x) функциясы берілсін. [a,b] кесіндісін кез – келген

a≤ x0<x1... xi< 1x<... ≤xn=b нүктелерімен бөліктерге бөлеміз. Әрбір [xi-1,xi] бөліктен қалауымызша [xi -1,xi], нүктелерін алып, интегралдық қосынды деп аталатын

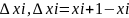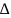S n(f)=∑f(€i) қосындысын құрамыз.µ= max xi белгілейміз. Егер lim Sn(f) шек бар болса, онда оны f(x) функциясының [a,b] кесіндісіндегі анықталған интегралы (Риман интегралы ) деп атайды. Мұндағы а мен b сандарын анықталған интегралдың сәйкес тӛменгі және жоғарғы шегі деп атайды. f(x) функциясы [a,b] кесіндісінде шектелген болсын. Онда mi = inf f(x), Mi = sup f(x) белгілер енгізіледі, мұндағы s және S қосындыларын Дарбудың сәйкес төменгі және жоғарғы қосындысы деп атайды.

Егер f(x) функциясы [a,b] үзіліссіз болса, онда Дарбу қосындылары интегралдық

қосындылардың ең үлкені және ең кішісі болады.

Сонымен, s Sn S

1 –теорема. [a,b] шектелген f(x) функциясының осы кесіндіде интегралдануы үшін

lim(S-s)=0 шартының орындалуы қажетті және жеткілікті.