
- •М огульський є. З., Бородай г.П. Математика для економістів. 2 семестр 2012р. Диференціальне числення функцій кількох змінних
- •1. Функції двох змінних та їх геометричне зображення
- •2. Частинні похідні
- •3. Диференціал функції двох змінних
- •4. Похідна за напрямом . Градієнт. Лінії рівня
- •5. Екстремум функції двох змінних
- •6. Умовний екстремум
- •Оскільки , , , то у загальному вигляді
- •Рівняння системи знайдемо , .Отже, стаціонарні точки функції Лагранжа є . Оскільки , , , то, як і у попередньому прикладі обчислимо у загальному вигляді
- •7. Метод найменших квадратів
- •8.Функции, применяемые в экономике. Предельный анализ. Эластичность
- •1.Функции, применяемые в экономике
- •2.Предельный анализ
- •3.Эластичность функции
- •4. Ценовая эластичность спроса
5. Екстремум функції двох змінних
Означення
точки локального максимуму (мінімуму)
функції
повністю збігається з означенням для
випадку функції однієї змінної: точка
є точкою локального
максимуму (мінімуму),
якщо існує такий проколений окіл
точки
,
що для всіх точок
![]() виконується нерівність
виконується нерівність
![]()
![]() .
.
Приклад
4. 1) точка
![]() є точкою локального мінімуму функції
.
Дійсно,
є точкою локального мінімуму функції
.
Дійсно,
![]()
![]()
(рис. 8.2).
2) точка
не є точкою локального екстремуму
функції
.
Дійсно, функція дорівнює нулю в точці
![]() ,
а в будь-якому околі
,
а в будь-якому околі
![]() цієї точки набуває як додатних, так і
від’ємних значень:
цієї точки набуває як додатних, так і
від’ємних значень:
![]() ,
,
![]() (див. рис. 8.4).
(див. рис. 8.4).
Теорема 1. (Необхідні умови існування локального екстремуму)
Якщо точка є точкою локального екстремуму диференційовної функції , то її частинні похідні першого порядку в цій точці дорівнюють нулю
-

(8.7)
Точки, координати яких задовольняють системі (8.7), називаються стаціонарними (критичними), в цих точках може бути екстремум.
Таким чином, точки локального екстремуму диференційовної функції можуть знаходитися лише серед її стаціонарних точок.
Легко бачити, що рівність нулю частинних похідних першого порядку у якійсь точці ще не означає існування екстремуму в цій точці.
Розглянемо,
наприклад, функцію
(підрозд. 1, рис. 4). Тоді
![]() ,
,
![]() і точка
і точка
![]() є стаціонарною, проте не є точкою
локального екстремуму.
є стаціонарною, проте не є точкою
локального екстремуму.
Теорема 2 (Достатні умови існування локального екстремуму)
Нехай точка є критичною точкою функції .
Складається
визначник
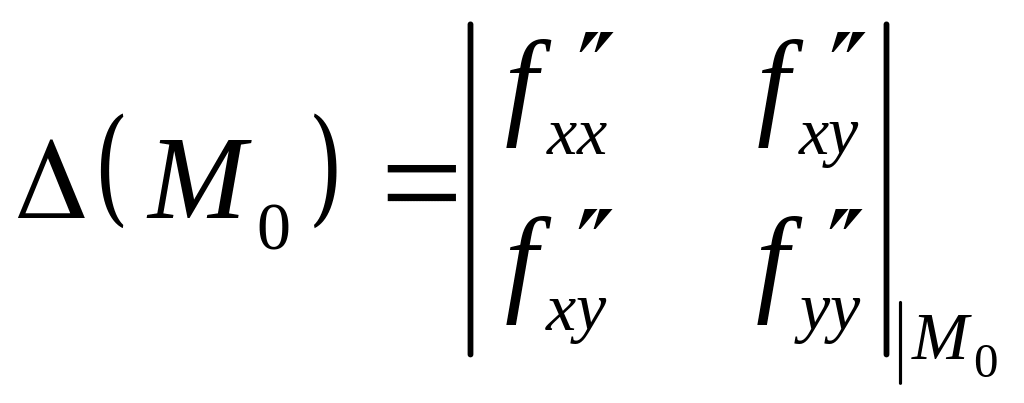 .
.
Тоді точка :
1) є
точкою локального мінімуму, якщо
![]() ,
,
![]() ;
;
2) є
точкою локального максимуму, якщо
,
![]() ;
;
3) не є
точкою локального екстремуму, якщо
![]() .
.
Зауваження.
Якщо
![]() ,
то відповісти на питання про наявність
екстремуму у точці
не можна і потрібні додаткові дослідження.
,
то відповісти на питання про наявність
екстремуму у точці
не можна і потрібні додаткові дослідження.
Приклад
5. Дослідити на екстремум
функцію
![]() .
.
Розв’язання. Знайдемо точки, у яких може бути екстремум. З цією метою розв’яжемо систему рівнянь (8.5)

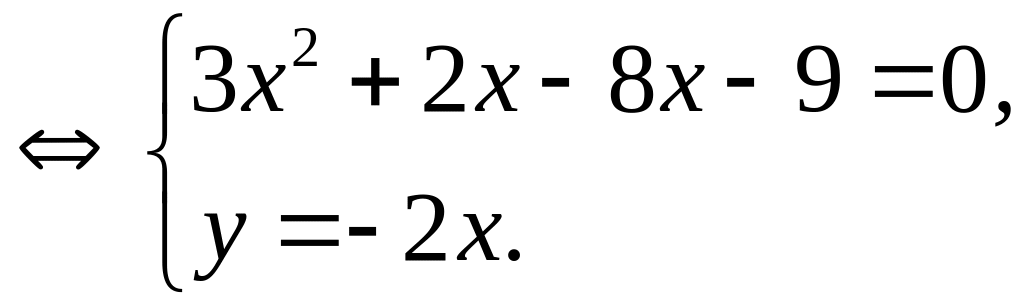
![]() ,
,
![]() .
.
З
останнього рівняння випливає, що ![]() ,
тоді
,
тоді
![]() .
Отже, маємо дві стаціонарні точки:
.
Отже, маємо дві стаціонарні точки:
![]() ;
;
![]() ..
..
Оскільки
![]() ,
,
![]() ,
,
![]() ,
то
,
то
 ;
;
 ;
;
У точці
![]() за правилом 3 теореми 2 екстремуму немає.
Оскільки
за правилом 3 теореми 2 екстремуму немає.
Оскільки
![]() та
та
![]() то за правилом 1 теореми 2 у точці
то за правилом 1 теореми 2 у точці
![]() локальний мінімум .
локальний мінімум .
![]() 27+9-72+36-27+5=–22.
27+9-72+36-27+5=–22.
6. Умовний екстремум
Задачі
знаходження екстремуму функції
не на всій області її визначення
![]() ,
а тільки на деякій лінії
,
а тільки на деякій лінії
![]() ,
рівняння якої
,
рівняння якої
![]() називаються задачами на умовний
екстремум.
називаються задачами на умовний
екстремум.
Рівняння називається рівнянням зв’язку
Означення.
Точка
називається точкою локального
умовного екстремуму
функції
відносно зв’язку
![]() ,
якщо
є точкою локального екстремуму функції
,
що розглядається тільки на лінії
,
якщо
є точкою локального екстремуму функції
,
що розглядається тільки на лінії
![]() .
.
Далі
припускаємо, що
![]() має в околі
має в околі
![]() точки
неперервні частинні похідні до другого
порядку включно та
точки
неперервні частинні похідні до другого
порядку включно та
![]() .
.
Задача на умовний екстремум розв’язується методом Лагранжа, який відіграє велику роль при розв’язанні важливих сучасних задач оптимізації та складається з наступних кроків.
1) складаємо допоміжну функцію трьох змінних (функцію Лагранжа)
![]() ;
;
2)
знаходимо частинні похідні цієї функції
за змінними
,
,
![]() ;
;
3) прирівнюючи до нуля знайдені в п. 2) похідні та розв’язуючи отриману систему рівнянь, знаходимо стаціонарні (критичні) точки (точки можливого локального екстремуму);
4)Нехай
![]() є стаціонарною (критичною) точкою функції
Лагранжа. Складається визначник
є стаціонарною (критичною) точкою функції
Лагранжа. Складається визначник
 .
.
Якщо
![]() ,
то функція
має у точці
,
то функція
має у точці
![]() умовний максимум.
умовний максимум.
Якщо
![]() ,
то функція
має у точці
умовний мінімум.
,
то функція
має у точці
умовний мінімум.
Приклад
6. Знайти екстремуми
функції
![]() при наявності зв’язку
при наявності зв’язку
![]() .
.
Розв’язання. Запишемо функцію Лагранжа
![]()
та
отримаємо необхідні умови екстремуму.
Якщо
![]() ,
то
,
то
![]() ,
що суперечить третьому рівнянню (рівнянню
зв’язку). Помножимо перше рівняння на
,
що суперечить третьому рівнянню (рівнянню
зв’язку). Помножимо перше рівняння на
![]() ,
а друге на
та
додавши перші два рівняння системи (2)
виключаємо з системи змінну
,
а друге на
та
додавши перші два рівняння системи (2)
виключаємо з системи змінну
![]()
 (1)
(1)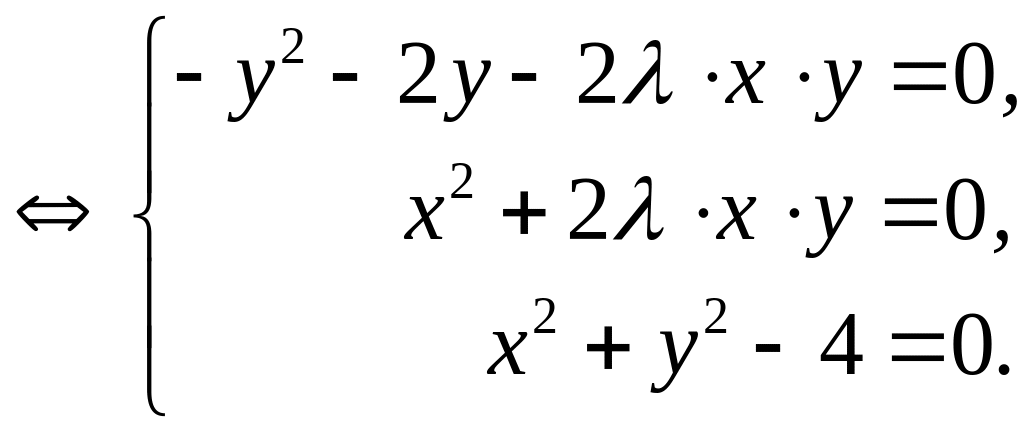 (2)
(2)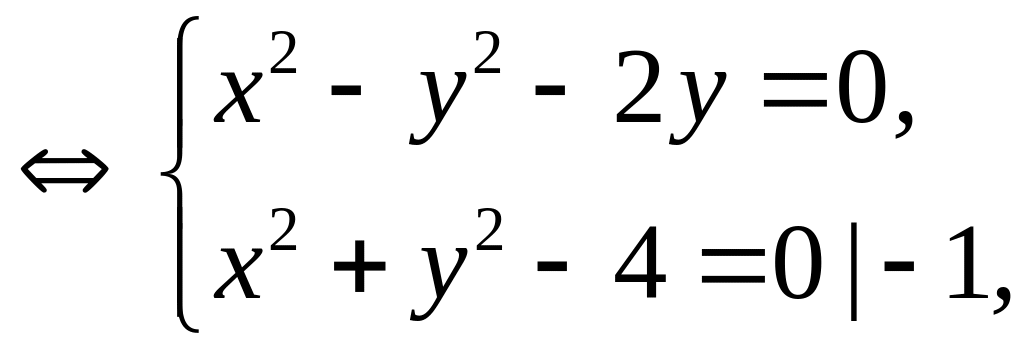 (3).
(3).
Помножимо
друге рівняння системи (3) на –1
та додаємо до першого. Одержано квадратне
рівняння
![]() або
або
![]() ,
корені якого
,
корені якого
![]() .
Для
.
Для
![]() з
другого рівняння системи (3) знайдемо
з
другого рівняння системи (3) знайдемо
![]() ,
а для
,
а для
![]() одержимо
одержимо![]() .
Тобто
.
Тобто
![]() а з першого або другого рівняння системи
(3) знайдемо
а з першого або другого рівняння системи
(3) знайдемо
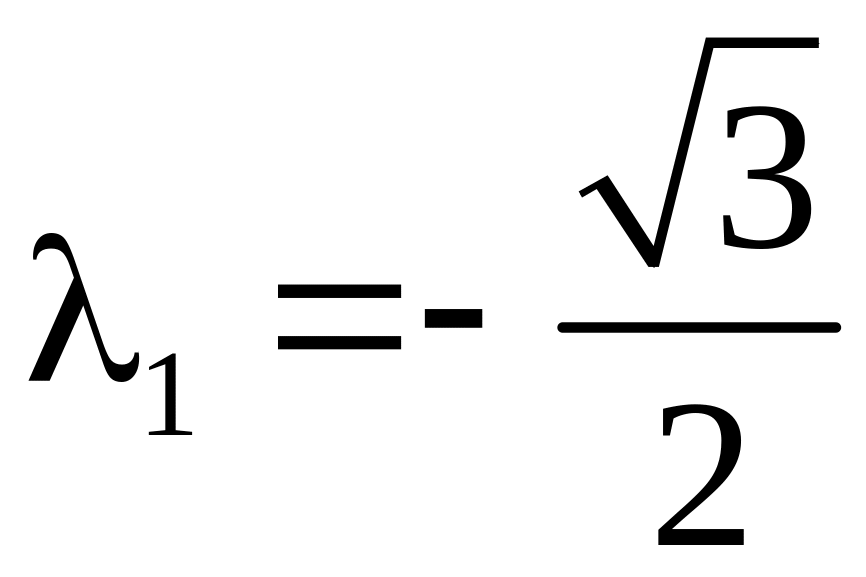 ,
,
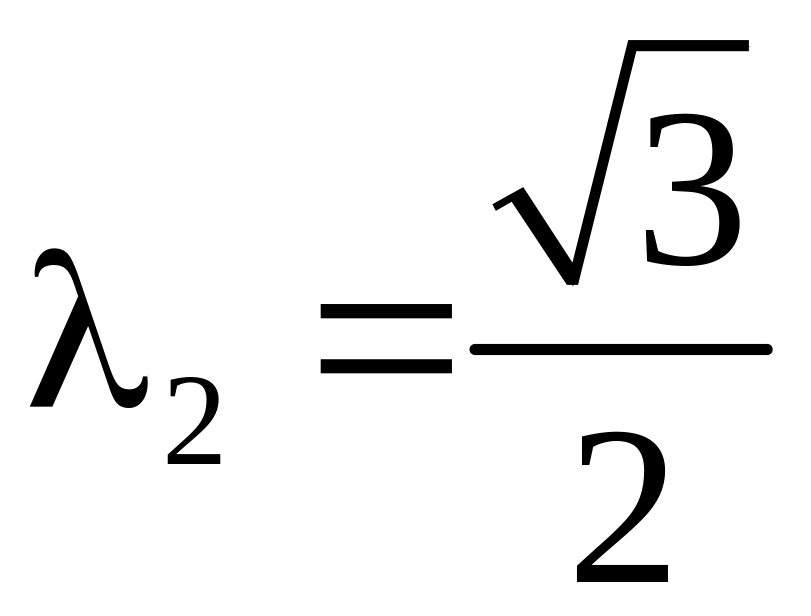 ,
,
![]() .Отже,
стаціонарні точки функції Лагранжа є
.Отже,
стаціонарні точки функції Лагранжа є
![]()
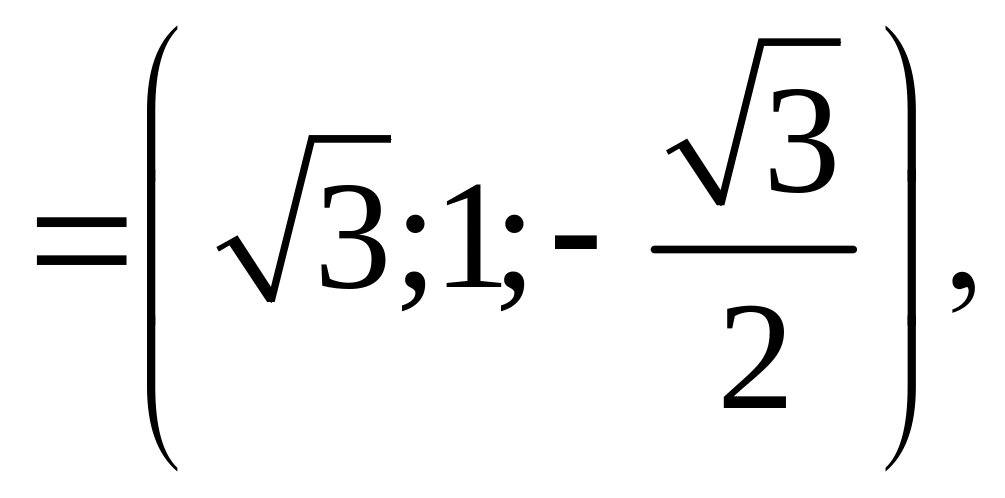
 .
.
