М огульський є. З., Бородай г.П. Математика для економістів. 2 семестр 2012р. Диференціальне числення функцій кількох змінних

У природознавстві і техніці часто зустрічаються випадки, коли одна величина залежить від двох чи більшої кількості інших величин. Наведемо приклади: відомий закон Бойля –­ Маріотта виражає залежність об'єму визначеної кількості газу від його тиску і абсолютної температури ; температура нерівномірно нагрітого тіла залежить від координат точки цього тіла.

1. Функції двох змінних та їх геометричне зображення

Нехай – деяка множина точок площини .

Означення 1. Якщо кожній точці ставиться у відповідність однозначно визначене число , то кажуть,що на множині задана числова функція двох змінних (функція точки) .

Аналогічно визначаються функції більшої кількості змінних.

Ф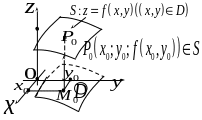 ункції двох змінних можна наочно зобразити за допомогою просторової системи координат. Графіком функції буде сукупність точок простору з координатами . Ці точки утворюють деяку поверхню , рівняння якої (рис.1, а).

а Рис.1

б

Н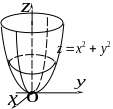 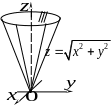априклад, графіком функції буде площина ; графік функції –параболоїд (рис.2); графік функції – верхня порожнина конуса (рис.3), а графік функції – сідло (гіперболічний параболоїд) (рис. 4).

Рис.2

Рис.3

Рис. 4

Поняття границі і неперервності функції двох змінних у точці вводиться абсолютно аналогічно тому, як це робилося у випадку функції однієї змінної. Єдине, що тут потрібно, це дати поняття околу точки .

Означення 2. Околом точки називається така сукупність точок , яка містить у собі деякий круг з центром у точці .

Проколеним околом точки називається окіл , за винятком самої точки (див. рис.1, б).

Означення 3. Число називається границею функції у точці , якщо для будь-якого околу числа знайдеться такий проколений окіл точки , що для всіх точок значення функції .

Інакше кажучи, , якщо від-

стань при будь-якому способі наближення точки до

точки .

Означення 4. Приростом функції у точці , який відповідає переходу до точки , називається величина .

Означення 5. Функція називається неперервною у точці , якщо існує такий окіл цієї точки, що значення функції у точках цього околу як завгодно мало відрізняються між собою: , якщо .