6. Соотношение неопределенностей Гейзенберга. Описание движения в квантовой механике.

НЕОПРЕДЕЛЁННОСТЕЙ СООТНОШЕНИЯ

- фундаментальные соотношения квантовой механики, устанавливающие предел точности одноврем. определения канонически-сопряжённых динамических переменных, характеризующих квантовую систему: координата - импульс, действие - угол и т. д. Математически Н. с. имеет вид неравенства, напр.

где D х и D р _х - неопределённости значений координаты х и сопряжённой ей компоненты р _х импульса р (аналогичные соотношения справедливы и для пар др. компонент координаты и импульса: у, р _у; z, p_z).

Н. с. были установлены В. Гейзенбергом (W. Heisen-berg) в 1927 при анализе мысленного эксперимента по измерению координаты квантового объекта с помощью "гамма-микроскопа" [1]. В 1929 X. П. Робертсон (Н. P. Robertson) показал, что Н. с.

являются следствием коммутац. соотношений (см. Перестановочные соотношения) между операторами и соответствующих физ. величин, причём Dx и D р _x в (1) определяются как среднеквадратичные отклонения:

где чертой обозначены средние от операторов, определяемые ф-лои

(y - волновая функция состояния, интегрирование производится по всему объёму, где y 0; звёздочкой помечено комплексное сопряжение). Он же доказал, что равенство в H. с..достигается только для квантовых состояний, к-рые описываются т. н. гауссовыми волновыми пакетами (см. Когерентное состояние). Э. Шрёдингер (Е. Schrodinger) предложил более общую ф-лу в случае т. н. коррелпров. состояний [2], для к-рых

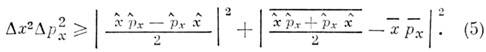
Если ввести коэф. корреляции r², равный отношению второго члена правой части к произведению D х^2.D р² _х, то Н. с. (5) примет вид

т. е. для сильно коррелированных состояний (r ~ 1) "эфф. постоянная Планка" может существенно превышать величину .

Соотношения типа (1) имеют место для любых физ. величин (f, g), к-рым соответствуют некоммутирующие эрмитовы операторы. Если коммутатор (где - эрмитов оператор), то Н. с. приобретают вид

[к-рый для коррелиров. состояний модифицируется аналогично (6)]. В частности, для проекций угл. момента , и поэтому

Среди физ. толкований Н. с. можно выделить по крайней мере три уровня, к-рым в англоязычной литературе соответствуют три разл. термина: uncertainty, indeterminateness, indeterminancy. Наиб. часто, особенно в упрощённых изложениях принципов квантовой механики, Н. с. (uncertainty relations) трактуют как ограничение на экспериментально достижимую точность измерения характеристик квантовых объектов, обусловленное неадекватностью классич. приборов целям квантовых измерений.

Др. толкование (indeterminateness) исходит из предпосылки, что Н. с. есть следствие свойства квантовых объектов, внутренне присущих им, независимо от несовершенства конкретных реализаций эксперим. установок, предназначенных для измерения этих свойств. Таким внутр. свойством является корпускулярно-волно-вой дуализм квантовых объектов, т. е. неразделимое сочетание волновых и корпускулярных свойств, равно необходимых для их полного описания. С этой точки зрения, аналоги Н. с. были хорошо известны, напр. в акустике и оптике, задолго до создания квантовой механики. Так, для цуга излучения протяжённостью D х, представляющего собой волновой пакет с волновыми числами, лежащими в интервале Dk, справедливы соотношения

к-рые с учётом квантового соотношения де Бройля р = k эквивалентны Н. с. (1).

Второе толкование Н. с. значительно шире и плодотворнее первого, поскольку оно представляет собой не частное утверждение о границах уточнения характеристик квантовых объектов, а гораздо более общий принцип неопределённости. Этот принцип по существу является предпосылкой статистич. интерпретации квантовой механики и важнейшим примером дополнительности принципа Бора (для этого расширит. толкования Н. с. часто используют термин indeterminancy). С точки зрения этого более общего принципа, Н. с. трактуются как способ сохранить клас-сич. понятия для описания квантовых систем путём взаимного ограничения области их совместной применимости.

Н. с. для энергии и времени t по форме совпадает с (1):

однако их толкование отличается от интерпретации соотношения (1). Обычно Н. с. (9) трактуются как невозможность точного определения энергии квантовой системы (D = 0) за ограниченный интервал времени Dt. В качестве иллюстрации Н. с. для пары и tH. Бор (N. Bohr) обращал внимание на невозможность определить понятие монохроматич. волны в данный момент времени.

Неопределённостей соотношение

        принцип неопределённости, фундаментальное положение квантовой теории, утверждающее, что любая физическая система не может находиться в состояниях, в которых координаты её центра инерции и импульс одновременно принимают вполне определённые, точные значения. Количественная формулировка Н. с.: если Δx — неопределённость значения координаты х, а (p_x — неопределённость проекции импульса на ось х, то произведение этих неопределённостей должно быть по порядку величины не меньше постоянной Планка ħ. Аналогичные неравенства должны выполняться для любой пары так называемых канонически сопряжённых переменных, например для координаты у и проекции импульса р_у на ось у, координаты z и проекции импульса p_z. Если под неопределённостями координаты и импульса понимать среднеквадратичные отклонения этих физических величин от их средних значений, то Н. с. имеют вид:

        

         Ввиду малости ħ по сравнению с макроскопическими величинами той же размерности действия (См. Действие) Н. с. существенны в основном для явлений атомных (и меньших) масштабов и не проявляются при взаимодействиях макроскопических тел.

         Из Н. с. следует, что чем точнее определена одна из входящих в неравенство величин, тем менее определённым является значение другой. Никакой эксперимент не может привести к одновременно точному измерению таких динамических переменных; при этом неопределённость в измерениях связана не с несовершенством экспериментальной техники, а с объективными свойствами материи.

         Принцип неопределённости, открытый в 1927 В. Гейзенбергом, явился важным этапом в уяснении закономерностей внутриатомных явлений и построении квантовой механики (См. Квантовая механика). Существенной чертой микроскопических объектов является их корпускулярно-волновая природа (см. Корпускулярно-волновой дуализм). Состояние частицы полностью определяется волновой функцией (См. Волновая функция). Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля. Поэтому результаты экспериментов по определению, например, координаты, имеют вероятностный характер. Это означает, что при проведении серии одинаковых опытов над одинаковыми системами получаются каждый раз, вообще говоря, разные значения. Однако некоторые значения будут более вероятными, чем другие, т. е. будут появляться чаще. Относительная частота появления тех или иных значений координаты пропорциональна квадрату модуля волновой функции в соответствующих точках пространства. Поэтому чаще всего будут получаться те значения координаты, которые лежат вблизи максимума волновой функции. Если максимум выражен четко (волновая функция представляет собой узкий Волновой пакет), то частица «в основном» находится около этого максимума. Тем не менее, некоторый разброс в значениях координаты, некоторая их неопределённость (порядка полуширины максимума) неизбежны. Тот же вывод относится и к измерению импульса.

         Т. о., понятия координаты и импульса в классическом смысле не могут быть применены к микроскопическим объектам. Пользуясь этими величинами при описании микроскопической системы, необходимо внести в их интерпретацию квантовые поправки. Такой поправкой и является Н. с.

         Несколько иной смысл имеет Н. с. для энергии Е и времени t,

        

        Если система находится в стационарном состоянии (т. е. в состоянии, которое при отсутствии внешних сил не изменяется), то из Н. с. следует, что энергию системы в этом состоянии можно измерить лишь с точностью, не превышающей

        

        где Δt — длительность процесса измерения. Причина этого — во взаимодействии системы с измерительным прибором, и Н. с. применительно к данному случаю означает, что энергию взаимодействия между измерительным прибором и исследуемой системой можно учесть лишь с точностью до

        

        (в предельном случае мгновенного измерения возникающий энергетический обмен становится полностью неопределённым). Соотношение

        

        справедливо также, если под ΔЕ понимать неопределённость значения энергии нестационарного состояния замкнутой системы, а под Δt — характерное время, в течение которого существенно меняются средние значения физических величин в этой системе.

         Н. с. для энергии и времени приводит к важным выводам относительно возбуждённых состояний атомов, молекул, ядер. Такие состояния нестабильны, и из Н. с. вытекает, что энергии возбуждённых уровней не могут быть строго определёнными, т. е. обладают некоторой шириной (так называемая естественная Ширина уровня). Если Δt — среднее время жизни возбуждённого состояния, то ширина его энергетического уровня (неопределённость энергии состояния) составляет

        

        Др. примером служит Альфа-распад радиоактивного ядра: энергетический разброс ΔЕ испускаемых α-частиц, связан с временем жизни τ такого ядра соотношением