22. Критерій Лапласа

Критерій Бернуллі-Лапласа використовують у випадку, коли можна припусти, що будь-який з варіантів середовища не більш ймовірний, ніж інший. Тут передбачається, що всі стани середовища (всі варіанти реальної ситуації) рівноймовірні.

Для кожної стратегії Аі (і -го варіанта рішення) слід розрахувати середній очікуваний доход (математичне очікування) за формулою (3.25), і відповідно до критерію Бернуллі-Лапласа слід вибирати варіант (стратегію Аi ), для якого досягається найбільше значення:

23. 23.Задача рішення

Задача рішення зі спостереженням (статистична задача рішення).

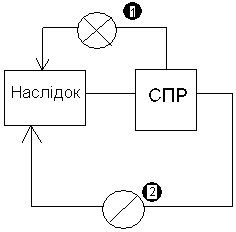
1 - ω ∈ Ω

2 - y=f₁(ω , ζ)

y=f₂(C, χ), χ- з перешкодами

Приклад

Експеримент Y – це величина, яка показує приблизне значення розподілу величини ω.

ξ - розподіл величини ω

Наприклад:

Ми їдемо в машині, маємо прийняти рішення: чи потрібно на даний момент часу заправити машину.

Невідома величина: ω – кількість бензину у баку (бак майже пустий або бензину трохи менше половини).

Значення апарату: y₀ –бак порожній y₁-бак напівпорожній y₂ –бак повний.

Ми звичайно просто можемо прийняти рішення: заправитись зараз, або до наступної заправки.

Але ми маємо апарат що міряє значення об’єму бензину.

Всі апарати недосконалі, і цей показує своє значення з певною похибкою, та ще машину трусить, тому він показує що бак напівпорожній (ω₂) – ймовірність цього (припустимо 70 відсотків).

Та можливо апарат бреше – тобто повністю порожній бак (ω₁) – ймовірність (1- ξ) 30 відсотків.

Тобто: Y-значення стрілки апарату, ω-фактичний об’єм бензину.

23. Система принятия решения и задача решения

еТеории управления (ТУ) и Теории решений (ТПР) базируется на близости понятий системы управления (СУ) и системы решений (СР). ТУ изучает СУ, состоящую из пары — объект управления и регулятор. ТПР изучает СР, состоящую из ситуации принятия решения и того, кто принимает решения. Проблема выбора действия, который приведет к некоторому последствию, возникает в обеих системах. В обеих системах можно выделить два главных усложнения выбора: динамика и неопределенность. Развитие ТУ началось в инженерии, и динамика объекта управления стала ее главной проблемой. В тоже время, развитие ТПР началось в экономике, и ее главной проблемой стала неопределенность.

Задача принятия решений (ЗПР) направлена на определение наилучшего (оптимального) способа действий для достижения поставленнях целей. Под целью понимается идеальное представление желаемого состояния или результата деятельности. Если фактическое состояние не соответствует желаемому, то имеет место проблема. Выработка плана действий по устранению проблемысоставляет сущность задачи принятия решений.

Проблемы могут возникать в следующих случаях:

- функционирование системы в данный момент не обеспечивает достижение поставленных целей;

- функционирование системы в будущем не обеспечит достижение поставленных целей;

- необходимо изменение целей деятельности.

Проблема всегда связана с определенными условиями, которые обобщенно называют ситуацией. Совокупность проблемы и ситуации образует проблемную ситуацию. Выявление и описание проблемной ситуации дает исходную информацию для постановки задачи принятия решений.

Субъектом всякого решения является лицо, принимающее решение (ЛПР). Понятие ЛПР является собирательным. Это может быть одно лицо – индивидуальное ЛПР или группа лиц, вырабатывающих коллективное решение, групповое ЛПР. Для помощи ЛПР в сборе и анализе информации и формировании решений привлекаются эксперты – специалисты по решаемой проблеме. Понятие эксперта в теории принятия решений трактуется в широком смысле и включает сотрудников аппарата управления, подготавливающих решение, ученых и практиков.

Принятие решений происходит во времени, поэтому вводится понятие процесса принятия решений. Этот процесс состоит из последовательности этапов и процедур и направлен на устранение проблемной ситуации.

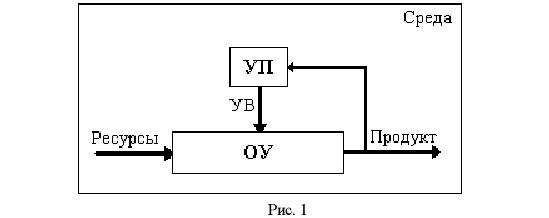
Руководствуясь этой формой, формальная модель ЗПР может быть описана следующим образом:

- для индивидуальногоЛПР

< So, T, Q | S, A, B, Y, f, K, Yopt >;

- для группового ЛПР

< So, T, Q | S, A, B, Y, F(f), L, Yopt >,

где слева от вертикальной черты расположены известные, а справа - неизвестные элементы задачи:

So – проблемная ситуация;

T –время для принятия решения;

Q – имеющиеся для принятия решения ресурсы;

S = (S1,..,Sn) – множество альтернативных ситуаций, уточняющих проблемную ситуацию So;

A=(A1,…,Ak) – множество целей, преследуемых при принятии решения;

B=(B1,…,BL) – множество ограничений;

Y=(Y1,…,Ym) – множество альтернативных вариантов решения;

f – функция предпочтения ЛПР;

K – критерий выбора наилучшего решения;

F(f) – функция групового предпочтения;

L – принцип согласования индивидуальных предпочтений для формирования группового предпочтения;

Yopt – оптимальное решение.

Таким образом, содержание задачи принятия решения можно сформулировать следующим образом:

в условиях проблемной ситуации So, располагаемого времени T и ресурсов Q необходимо уточнить ситуацию So множеством гипотетических ситуаций S, сформировать множества целей A, ограничений B и альтернативных вариантов решения Y, произвести оценку индивидуальных предпочтений решений f и найти оптимальное решение Yopt, руководствуясь сформулированным критерием выбора K - для индивидуального ЛПР, или удовлетворяющее групповому предпочтению F(f), найденному на основе выбранного принципа согласования L - для группового ЛПР.