5.Перехід від матричної моделі до лотерейної

Необхідно перетворити матричну модель в лотерейну, тобто яка складається з лотерейної схеми 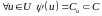та інформації .Треба побудувати відображення , яке буде задовольняти умові

Маємо:

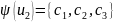
Тепер треба перенести інформацію. При дії 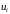наслідок наступає при будь-якому значенні параметра , для якого 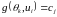. Тому розумно встановити між розподілами 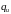і таку залежність

Оскільки ми вважаємо, що є тільки одне істинне значення параметра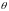 , то події є несумісними, а отже для будь якої їх суми справедливо

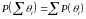
Тому

Таким чином:

0,6

Дискретні розподіли:

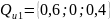
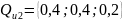
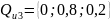
7. Невизначеність у СПР

Невизначеність у ЛСПР існує, якщо:

- Дві різні дії призводять до таких самих двох різних наслідків

- Якщо одна дія призводить до двох деяких наслідків, а інша до хоча б одного наслідку, відмінного від попередніх.

Це справедливо, якщо ми не фіксуємо Відношення Переваг на Наслідках для ТПР.

В разі, якщо існує порядок на наслідках, необхідною і достатньою умовою невизначеності буде:

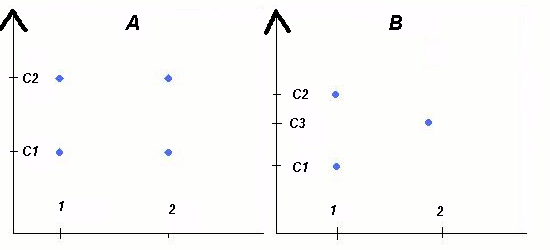
• За означенням невизначенності: "Коли два ТПР, з однаковими відношеннями переваг оберуть дві різні дії"

• У варіанті B Перший ТПР обере дію 1, бо може отримати максимальний виграш - С2, а Другий ТПР обере дію 2, бо не схильний до ризику і надає перевагу гарантованому виграшу С3

• У варіанті А, на перший погляд, дві дії еквівалентні, оскільки мають однакові наслідки. АЛЕ: завжди будуть ТПР1 та ТПР2, для яких виграш(1)>виграш(2) та виграш(1)<виграш(2) відповідно. І той та інший буде мати рацію.

Алгоритм Перевірки на невизначенність:

1)шукаємо дію (for по всіх таких діях), в якої>1 наслідку.

2) якшо 2 наслідки: шукаємо іншу дію (<> наша знайдена).

2а) якшо в неї є два наслідки, які такі ж як і наші два насліки, то ситуація невизначена.

2б) якшо в неї є наслідок, якого немає серед наших наслідків, то ситуація невизначена.

3) якшо >2 наслідків:

3а) шукаємо іншу дію (не наш знайдений) в якго є ХОЧ ОДИН наслідок. якшо знаходимо -- є невизначеність.

8. Усі багато чисельні взаємозв’язки між ознаками, котрі характеризують соціально-економічні явища і процеси, можна поділити на дві  групи: функціональні (детерміновані) і стохастичні (ймовірносні або кореляційні) зв’язки.

Функціональні (детерміновані) зв’язки характеризуються тим, що одному значенню факторної ознаки (Х) відповідає одне строго визначене (детерміноване) значення результативної ознаки (Y).  Ці зв’язки завжди є повними, тобто значення результативної ознаки на 100% залежить від факторної. Наприклад, тарифний денний заробіток (Y) при фіксованій годинній тарифній ставці залежить від кількості відпрацьованих годин (Х).

 

При стохастичному (кореляційному) зв’язку одному значенню факторної ознаки (Х) може відповідати декілька значень результативної ознаки (Y). Важливою особливістю цих зв’язків є те, що вони мають риси статистичної закономірності та проявляються у масі спостережень, при достатньо великій чисельності сукупності. Названі зв’язки є неповними, тому що завжди існують невраховані фактори, отже значення Y залежить від значень Х менше, ніж на 100%.  

Ймові́рність (лат. probabilitas, англ. probability) — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Імовірність є основним поняттям розділу математики, що називається теорія імовірностей.

Випадковою подією називається подія, результат якої не може бути відомий наперед. Навіть у тому разі, коли насправді подія детермінована своїми передумовами, вплив цих передумов може бути настільки складним, що вивести з них наслідок логічно й послідовно, неможливо. Наприклад, при підкидуванні монети, сторона на яку монета впаде визначається положенням руки і монети в руці, швидкістю, обертовим моментом тощо, однак відслідкувати всі ці фактори неможливо, тому результат можна вважати випадковим.

Існують два підходи до означення імовірності: математично-аксіоматичний і Баєсів. Аксіоматичний підхід, строго сформульований Колмогоровим, будується на припущенні, що імовірності елементарних випадкових подій задані, і зосереджується на визначенні ймовірностей складних подій, що є сукупністю елементарних. Так, наприклад, при підкидуванні шестигранного кубика гральної кості, ймовірності випадіння будь-якого числа, вважаються однаковими й рівними 1/6. Виходячи з цієї аксіоми, теорія ймовірності може розрахувати ймовірність того, що сума чисел на двох костях буде, наприклад, 8.

Баєсів підхід не робить припущень про ймовірності елементарних подій, а намагається отримати їх із аналізу попереднього досвіду, спираючись на теорему Баєса і на попереднігіпотези. Баєсів підхід ближчий до того, як визначаються імовірності випадкових подій у природознавстві. Оскільки ці ймовірності наперед невідомі, результати серії дослідів розбиваються на сприятливі й несприятливі, і експериментально визначена ймовірність дорівнює відношенню числа сприятливих подій до числа дослідів, тобто частоті подій.

Найпростіший тип зв’язку - детермінований , коли кожна альтернатива приводить до одного наслідку. В цьому випадку існує функціональна залежність між альтернативою x і наслідком z . Такі ЗПР називаються детермінованими.

2)Не детермінований тип, тобто кожній альтернативі відповідає не один і той самий наслідок. Якщо відомо з якою ймовірністю кожній альтернативі буде відповідати наслідок , тоді маємо статистичну заленість між x й z . В цьому випадку ЗПР називається задачею в умовах ризику або стохастичної невизначеності.

3)ЗПР проходить в умовах невизначеності, тобто відображення між множинами X та Z неоднозначне, але статистична залежність відсутня. Тут існують два випадки:

- якщо S поводить себе пасивно до ОПР(є проявом стихії, природи), то маємо ЗПР в невизначених умовах.

- якщо S поводить себе активно до ОПР, тобто приймає участь інша особа, тварина і т.д. ЗПР в умовах конфлікту (гри).

4)Якщо хоч одна з множин є нечіткою, чи нечітким є відображення X × S → Z тоді кажуть, що ПР проходить в умовах нечіткої інформації .