33. Побудова байєсівських вирішуючих функції екстенсивним методом

Нехай маємо умову:

Задача:

знайти, при якому розподілі величини ω1 та ω2 рішення d1 (ω2) , буде байєсівським d*.

Розв"язок:

визначимо розподіли ω1 та ω2:

P(ω1) = ξ P(ω2) = 1-ξ

1)

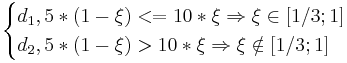
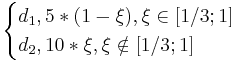
значення експериментів y1, y2 спостереження випадкової величини w1, w2:

34 Теорема виражена т.з. формулою Байєса 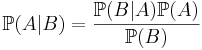 , де

• P(A) — апріорна ймовірність гіпотези A;

• P(A | B) — ймовірність гіпотези A за умови, що відбулась подія B (апостеріорна ймовірність);

• P(B | A) — ймовірність того, що відбулась подія B за умови істинності гіпотези A;

• P(B) — ймовірність того, що відбудеться подія B.

Тут «гіпотеза» – подія, яка за нашим припущенням причинила появу даної події.

Важливим наслідком формули Байєса є формула повної ймовірності події, що залежить від кількох несумісних гіпотез (і тільки від них!) 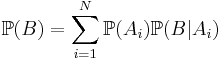 - ймовірність того, що відбудеться подія B, яка залежить від ряда гіпотез Ai, якщо відомі степені достовірності цих гіпотез (наприклад, заміряні експериментально)

 Нехай А і В— випадкові події, що мають ймовірності Р(А) > 0 і Р(В) > 0 відповідно. Позначимо через Р(АВ) ймовірність суміс­ного здійснення подій А і В, і нехай Р(А/В) — умовна ймовірність А, якщо відомо, що В вже відбулась. Тоді        , тобто  .             Отже, якщо В₀,В₁,... — події, що попарно не перетинаються та мають додатні ймовірності, і одна з них відбувається завжди (або принаймні з імо­вірністю 1), то            _.

Це і є формула Байєса. Вона показує, як за апріорними ймовірностями Р(В_к) (ймовірностям подій В_к до того, як подія А відбулася) знайти апостеріорніймовірності (після того, як подія А відбулася). Якщо розглядати події В_к як причини, то формула Байєса являє собою теорему про ймовірності при­чин. 

35 Лема Неймана –Пірсона.

Нехай і - задані постіними, і -рішаюча функція така що

, якщо

якщо

У випадку якщо в якості можна взяти будь-яке значення. або .

Тоді для будь-якої рішаючої функції

Доведення. Якщо - інша рішаюча функція, то нехай і підмножини виморочного простору , і визначаються наступним чином:

Тоді

Оскільки будь-яка рішаюча функція задається указанням множини , на якій вона приймає значення , то знаходження рішаючої функції мінімізуючої лінійну комбінацію , рівносильно визначенню множини , для якої останній інтеграл приймає найменше значення. Цей інтеграл досягає мінімуму , коли множина включає всі точки , для яких інтегральна функціє набуває відємного знаку, і не включає тих точок в яких підінтегральна функція додатня. При цьому не грає ролч чи входять точки рівні 0. Рішаючи функція , визначена за допомогою множини задовільняю умови 2 і 3.

36. Опуклі функції. Нерівність Єнсена

О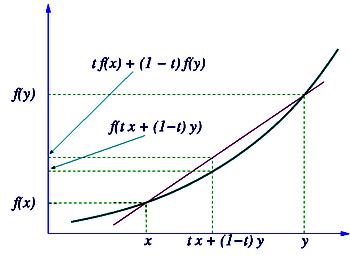 пукла функція — функція, яка визначена на опуклій множині лінійного простору, і задоволняє нерівності

при всіх λ [0, 1].

Нехай область визначення опуклої функції f(x) лежить в скінченовимірному просторі, тоді f(x) неперервна в будь якій внутрішній точці цієї області.

Нехай x₁, ..., x_m — будь які точки із області визначення опуклої функції f(x), λ₁, ..., λ_m — невід'ємні числа, які в сумі дорівнюють 1. Тоді

Якщо f(x) — двічи неперервно диференційована опукла функція, то матриця її других похідних напівдодатньо визначена.

Нерівність Йєсена

Нехай функція опукла вниз. Тоді для будь-якої випадкової величини ξ зі скінченним першим моментом

Лема

Нехай функція опукла. Тоді для будь-якого у знайдеться число с(у) таке що при всіх х .

Доведення

Візьмемо в умовах леми . Тоді .Обчислимо математичне сподівання обох частин нерівності. Оскільки, і нерівність між математичними сподіваннями зберігається із наслідку (1), тоді

Наслідок (1):

Наслідок математичного сподівання:

• Якщо ξ ≤ η, тоді Mξ ≤ Mη

• Якщо ξ ≤ η, і при цьому Mξ = Mη тоді ξ ≤ η

Нерівність Йeнсена , - опукла, , , , має місце нерівність .

Д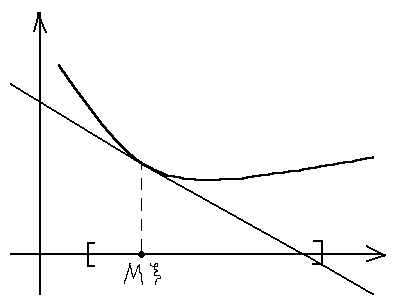 оведення: Оскільки , . Проведемо дотичну в точці до функції : .

Кінець доведення.

Якщо функція сильно опукла , то знак заміняють на .

Якщо функція опукла вгору, то знак заміняють на протилежний.

Наслідок Нехай - середній прибуток( - прибуток), якщо - інтерпритувати як виграш гравця в деякій грі і функція корисності гравця опукла(сильно опукла), тоді згідно нерівності Йенсена і нехай маємо гру, в якій , то ця нерівність доводить, що гравець, у якого функція корисності опукла буде грати. А для гравця, у якого функція корисності опукла вгору, маємо і він грати не буде.

37, Плата за експеремент

38, Той хто приймає рішення та його математична модель.

Поняття про модель Того, хто приймає рішення (ТПР).

1)Будуємо відношення переваг на наслідках β_c   b_c   Β_c

Β_c - всі можливі відношення переваг на множині С

b_c - всі відношення переваг на С, про які має уявлення ТПР

β_c - обране ТПР'ом відношення переваг

2)Знаходження оптимальног наслідку с₀   С

3)Побудова відношення переваг на діях:

β_D   b_D   Β_D

4)Оптимізація найкращого D:

β_D   найкраща дія

•  π:(M x b_c)   b_D - людина-проектор, π   П Э П_i - класи людей

• β_c   b_c ТПР(b_c, b_D, π) - модель ТПР

Особо важную роль играют психологические факторы в не- структуризованных проблемах, где имеются лишь качествен­ные, недостаточно определенные зависимости между основными переменными. Как человек анализирует эти проблемы? Как ЛПР учитывает недостаток информации? Ответы на эти вопро­сы частично содержатся в качественной модели ЛПР.

Черты человеческой системы переработки информации

 Человек имеет ограниченный объем кратковременной памяти; он не может уделять одновременно внимание многим аспектам, влияющим на принимаемое решение (см. лекцию 5).

Особенно ярко это ограничение проявляется при принятии новых решений (в отличие от повторяющихся), когда человек не может путем постоянных тренировок расширить возможности своей памяти, выработать определенную внутреннюю структуру хранения информации. Следствием этого ограничения являются известные случаи, когда ЛПР сознательно упрощает ситуацию, превращает часть критериев в ограничения, уменьшает число возможных оценок, группирует альтернативы и т.д.

 Человек минимизирует (подсознательно) свои усилия при поиске решения. Он меняет свои стратегии по ходу решения задач, выбирая те из них, которые требуют меньше умственных усилий (см. лекпию 5). Человек стремится использовать более про­стые когнитивные операции (например, сложение), простые сравнения малого числа переменных и т.д.

.