27,Рандомізація у теорії ігор та теорії рішень.

В задачах рішення часто буває дійсним припущення, що рішення d є D вибирається за допомогою додаткової процедури, наприклад, підкидаючи монету. Тобто, приймається змішане рішення – спочатку рішенням приписуються ймовірності, а тоді, згідно з цими ймовірностями, вибирається одна з них.

В таких випадках, втрати цього рішення, згідно з припущенням про середню корисність будуть вираховуватися так: L(w,d)=SUM_{_i=1}^INF [p_i * L(w,d_i)]. (1)

Якщо простір подій незліченний, то рандомізовані рішення можна позначати більш загально – якийсь розподіл на сігма-алгебрі, підмножин множини D.

Рандомізовані рішення позначаються М. тоді зрозуміло, що чисті рішення входять в рандомізовані (D є M): вистачає поставити ймовірності при всіх рішеннях 0, крім того, яке ми хочемо подати. (якщо є D={d₁,d₂,d₃}, то рішення m є M подається як (m=α*d₁+β*d₂+(1- α- β)*d₃). m, відповідне чистому рішенню d₁: m=1*d₁+0*d₂+0*d₃.)

Стосовно рандомізованих рішень важливим є твердження, що рандомізовані рішення не можуть зменшити мінімальний ризик, який було знайдено на чистих рішеннях.

Згідно з формулою (1), ризик рандомізованого рішення – це середньозважений ризик, розрахований з функцій втрат чистих рішень. З цього випливає, що, якщо існує ризик ρ(P,d) змішаного рішення, то його значення дорівнює суміші ризиків ρ(P,d_i) чистих рішень d_i.

З чого випливає, що

Inf_dєM [ρ(P,d)] = inf _dєD [ρ(P,d)] =ρ^*(P).

Тобто якщо є відрізок, то мініум його лежить на кінцях, і ніяк не можу бути на середині. Тобто, фактично, рандомізовані рішення задають всі можливі комбінації чистих рішень (з 2-х рішень роблять відрізок, з більше – якусь фігуру, а ця площина, що утворюється (гіперплощина у вищих просторах) не може виходити за межі твірних точок, якими і є чисті рішення.

27 Рандомизация и смешанные решения

В задачах решения является довольно полезным (и безусловно реалистическим) допущение о том, что статистик может выбрать решение из D с помощью той или иной вспомогательной процедуры рандомизации, например подбрасывания монеты. Другими словами, статистик может принимать смешанное или рандомизованное решение d, заключающееся в том, что сначала он приписывает вероятности p₁, p₂, … элементам некоторой последовательности d₁, d₂, … решений из D, а затем выбирает одно из решений d_i согласно этим вероятностям. Если ущерб L(ω,d), отвечающий смешанному решению d, существует при , то, согласно предположению о средней полезности, его значение равно

(1)

Для каждого распределения P параметра W и всякого смешанного решения d риск ρ(P,d) в случае его существования может быть определен той же формулой:

В задачах, где пространство решений D содержит нечетное число элементов, рандомизованное решение можно определить более общим образом при помощи произвольного вероятностного распределения на некоторой σ-алгебре множества D.

Пусть М обозначает множество всех смешанных решений данной задачи. В отличие от смешанных решений, решения из D называются чистыми. Всякое чистое решение d можно рассматривать как рандомизованное посредством тривиальной рандомизации, при которой чистое решение d выбирается с вероятностью 1. При таком соглашении 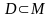. Вводя смешанные решения, мы заменяем, таким образом, пространство решений D более широким пространством M. Однако это расширение пространства решений никак не позволяет уменьшить риск статистика, так что нет особой нужды рассматривать решения, не входящие в исходное пространство D.

Для всякого распределения P параметра W статистику следует выбирать, если это возможно, решение , минимизирующее риск ρ(P,d). Согласно формуле (1), функция потерь для всякого смешанного решения d является смесью (взвешенным средним) функций потерь, отвечающих чистым решениям d_i (i=1, 2, …). Поэтому если риск ρ(P,d) смешанного решения существует, то его значение равно смеси рисков ρ(P,d_і) чистых решений di. Отсюда следует то, что

(2)

Из соотношения (2) видно, что никакому смешанному решению из М не отвечает риск, меньший, чем минимальное значение и независимо от того, достигается ли это значение на каком-нибудь элементе или нет. Если байесовский риск конечен и достигается при некотором смешанном решении ил М, то из предыдущих замечаний следует, что это же значение достигается и при некотором чистом решении из D.

28.